Оглавление:









Ламинарный перенос тепла на вертикальной пластине и горизонтальной трубе
- При естественной конвекции газа или жидкости, вызванной только разницей температур, на поверхности твердого тела также образуется пограничный слой. Из-за медленной скорости движения толщина границы cjfbn больше толщины, встречающейся в рассмотренных до сих пор примерах. Как рассчитать теплопередачу В естественной конвекции уравнения импульса и теплового потока в пограничном слое могут быть применены снова.
Этот раздел позволит решить самые простые задачи, связанные с вертикальной плитой*. Когда такая плита нагревается, температура газа или жидкости вблизи ее поверхности повышается, и газ или жидкость начинает подниматься. За счет этого на поверхности образуется пограничный слой, толщина которого начинается от нуля внизу в конце» th » пластины она увеличивается в направлении потока. Расстояние от нижней кромки пластины равно x, а расстояние от поверхности пластины равно y. Внутри пограничного слоя температура падает от значения, связанного с поверхностью пластины, до температуры газа или жидкости вне зоны нагрева. Пусть температура пластин будет одинаковой и постоянной на всем протяжении Температура и скорость при естественной конвекции вдоль вертикальной стенки. Поверхность.
Важно, что данное определение внутренней энергии справедливо для открытых систем. Людмила Фирмаль
Указывает на эту разницу в количестве Температура среды вне пограничного слоя показывает разницу между температурой любой точки в пограничном слое и температурой среды вне пограничного слоя В С. Температурное поле вблизи поверхности пластины должно иметь форму, показанную на рисунке. 11-1. In на этом графике d — толщина пограничного слоя. Скорость работы СМИ. На поверхности пластины и за ее пределами пограничный слой должен быть равен нулю. Поэтому поле скоростей имеет вид, показанный на рисунке. 11-1. To решая уравнение пограничного слоя, будем считать, что кривая распределения температуры имеет вид параболы. «= » (! — Ф. «) (1×1).
Это уравнение удовлетворяет граничным условиям к = КА для y = 0, 0 = 0 при г ->. 1. Аналогичный расчет для газа приводится в книге С. Гольдштейна „современный прогресс в гидродинамике“ (Оксфорд, Нью-Йорк, 1938) [l. 149]. Кривая распределения скоростей 11-1 на рисунке описывается следующим уравнением В) 2 Указывает любую функцию с размером скорости. Максимальное значение скорости по этому уравнению на расстоянии y =от стенки. 4. Его значение равно » max =uᵥ. Предполагается, что гидродинамический и термический пограничные слои имеют одинаковую толщину.
Обоснованность этого предположения подтверждается тем, что результаты расчетов, выполненных на основе таких предположений, полностью согласуются с экспериментальными данными[l. [195]. Недавно был проведен анализ, который использовал различную толщину пограничного слоя в полях скорости и температуры[l. [196] результаты немного отклонились от результатов, показанных здесь. Уравнение импульса (6-8) требует введения члена, представляющего подъемную силу. Эта сила составляет ГПП на единицу volume. In объемный элемент высотой dx и длиной i (больше толщины пограничного слоя, см. Рис. 7-2) 、 Мощность dxgfi j $ dy составляет effective.
To включите этот член в равенства-b В Формуле (6-8) низкоскоростная характеристика свободной конвекции предполагает, что давление постоянно и скорость вне пограничного слоя равна нулю, получаем формулу: Уравнение теплового потока (7-2) остается прежним. Здесь температура заменяется разницей температур. «Формула (11-3) и интеграл от (11-4) имеют вид、 Назовем уравнения поля температуры и скорости (11-1) и (11-2: ООО. Уравнения пограничного слоя В следующем формате: Я умею писать. _ _ _ _ 30. Чтобы решить эти уравнения, выразим u и o как экспоненциальную функцию x. Подстановка этих выражений обеспечивает: 2Т 4-р 105. Г » г » __〜а ^ ~ ~ п — Л. • С. С.
Эти уравнения должны быть действительны для любого x, поэтому экспоненты должны иметь одинаковое значение для каждого члена. 2М 4 ′ фут-Н = м-н м + п-1 = — н. Отсюда / Н = 1/2 и / г = 1/4. Подставляя эти значения в уравнение, получаем: £1£l₌ ₌ o3 {}£? __- 2Д 84 ш ь ся ’ 40 —c₂ Или Затем определите максимальную скорость в пограничном слое. «Максимум= 4i — ⁼ ⁼ ⁼» (°’⁹⁵2+ t)2(£^)2^(1、- thickness > и толщина пограничного слоя: 8 = 3. 93 ^)2(0. 952 + * /。 (11-6) В этом случае удобно придать этому значению безразмерный характер, разделив толщину пограничного слоя на расстояние х от нижнего края пластины.
Далее, знаменатель grₓ=, представлены в виде разности температур, появляется в этом уравнении Плита и газ или жидкость и расстояние x [справочная формула (9-19) ], и критерий Прандтля pr = y:. 2. 2. _Л * 4 — = 3. 93pg2 (0. 952 + pr) ⁴ (grj⁴. (11-7) Тепловой поток с поверхности пластины определяется соотношением Что получается из уравнения (11-1) : С другой стороны, для нахождения теплового потока существует формула, по которой можно определить коэффициент теплопередачи. Отсюда 7 = ав Причем в безразмерном виде Заменяя толщину пограничного слоя, он выглядит так: j_ 1_ nuₓ=0. 508pr2 (0. 952 4-pr) ⁴ (gr /. (11-9) ) Согласно формулам (11-6) и (11-8), локальное значение коэффициента теплопередачи обратно пропорционально 4-му корню из x.
Найти среднее значение коэффициента теплоотдачи, после интегрирования в диапазоне 0-x. −4. 。. .а-₃a .Это означает, что среднее значение коэффициента теплопередачи вертикальной пластины на высоте x равно ⁴ / ₃ локального значения коэффициента в точке X . Для идеального газа справедливо соотношение p = 1 / G .Если разница температур небольшая, можно записать P = 1 / Гwrite .Где Т0-абсолютная температура газа вне пограничного слоя .Prandt-la стандартный воздушный корпус Pr = 0, 714 Нуₓ= 0, 378 (Гᵣ/* .(11-10) В случае этой среды теплопередача осуществляется по Э . Шмидту и В . Э .в сотрудничестве с Beckman .It был точно рассчитан порхаузеном [L .[197] в результате этой работы мы выяснили, что в Формуле (11-10) вместо коэффициента 0, 378 нам нужно подставить число 0, 360 .
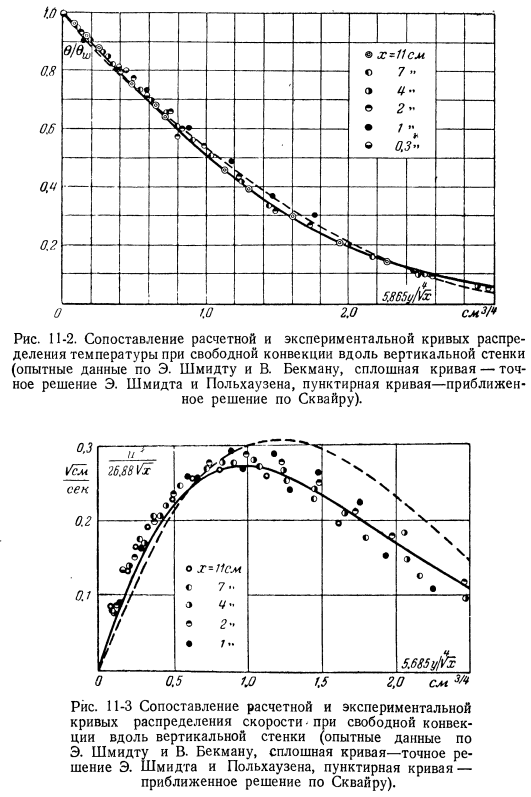
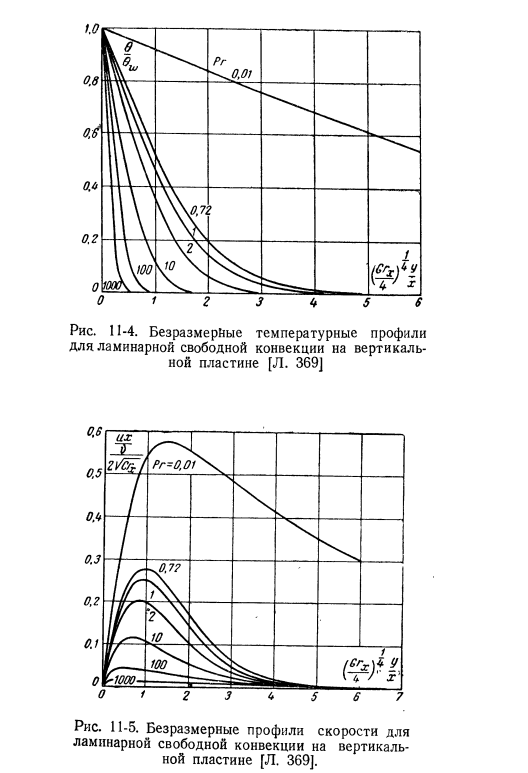
Из этого мы видим, что приблизительный расчет достаточно хорошо согласуется с результатами точного расчета, который является трудоемким .Значение, рассчитанное по приведенной здесь формуле, и в результате проведенных экспериментов и расчетов Э . Шмидта и В .сравнение со значениями, полученными Бекманом, показано на графике на Рис .2 .11-2 и 11-3 .In в ходе расчетов значения физических параметров определялись по температуре пластин .С . Острак . 198]недавно для некоторых чисел Прандтля мы решили уравнение ламинарного пограничного слоя свободной конвекции вертикальной пластины на компьютере .
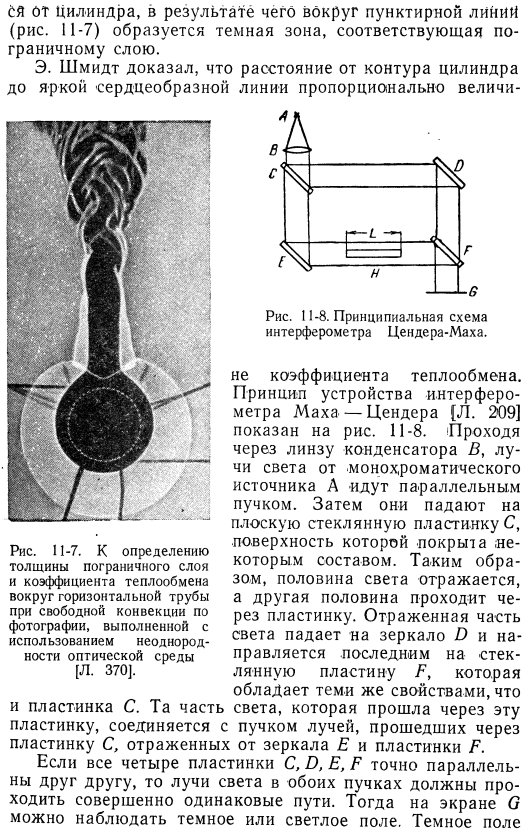
Результирующий профиль скорости и температуры показан на рисунке .11-4 и 11-5 .Число нуссельцев, полученное в результате этого анализа, совпадает с числом, рассчитанным по формуле (11-9), с погрешностью около 10%в диапазоне числа Рисунок 11-2 .Сравнение расчетных и экспериментальных кривых распределения температуры при естественной конвекции вдоль вертикальной стенки (Э . В . Шмидт .Экспериментальные данные по Бекману, кривая сплошной линии-это е .точное решение Шмидта и Полхаузена, пунктирная кривая-приближенное решение Сквайра) .Инжир .11-3 расчет свободной конвекции вдоль вертикальной стенки и сравнение экспериментальной кривой распределения скоростей (Э . Шмидт и В .экспериментальные данные Бекмана, кривая сплошной линии-точное решение Шмидта и порхаузена, кривая ломаной линии-приближенное решение Сквайра) .Рис .11-4 .
Ламинарная свободная конвекция безразмерный температурный профиль на вертикальной пластине[L .369 .] Рисунок 11-5 .Профиль скорости ламинарной свободной конвекции на вертикальной пластине[L .369] .Прандтля от 0, 01 до 1000 .Это решение дает гораздо лучшие результаты, чем выражение Nu neg = ’ C (GrrPr), чем .Это достигается путем суммирования экспериментальных данных по воздуху в предположении пренебрежения инерцией[уравнение (9-19) ] .Э . Шмидт и В . Бекман, И . Э .Эккерт и Saengen Е .[199] в воздухе и X . X . Лоренцов (L .200) и О . А .Сандерс [L .201] в масле и ртути также теоретически хорошо совпадают .Рис .11-6 .Горизонтальные трубы и вертикальные плиты с одинаковым средним коэффициентом теплопередачи для свободной конвекции 5 .
- Просто так В .ми .Результат .Кроме вертикальных стенок, очень важен также вопрос о горизонтальных трубах[L .202] .в этом случае уравнение пограничного слоя является немецким [L .[203] .Результаты расчетов Германа хорошо согласуются с экспериментальными данными Йодльбауэра[L .204] .На основании этих исследований можно сделать следующее обобщение: среднее значение коэффициента теплопередачи круглой трубы поперечного сечения диаметром d равно среднему значению коэффициента теплопередачи вертикальной стенки 2, 5 ^высокой (рис .11-6) .Ром, несправедливость .
Однако расчет пограничного слоя был выполнен с помощью Herman .To учитывают этот фактор Ленгмюр [L .205] и Райс[L .206] .Для пограничного слоя используйте неподвижный воздушный цилиндрический слой вокруг проволоки .Через этот слой теплопередача от проволоки происходит только за счет теплопроводности .Поэтому формулы (3-6) и (3-7) определяют этот тепловой поток .Где n равно радиусу проволоки (диаметр принимается равным d = 2r) . / g — ’ температура проволоки и / o-температура наружного пограничного слоя .С другой стороны, равенство, основанное на рассматриваемых условиях, является: Q = a2w / ( / ; — Q) .
Если правая часть уравнения равна правой части уравнения (3-7), то: И затем Два Так .. Где b = ri-rn-толщина пограничного слоя, который вы приняли. Эта толщина определяется таким образом, что последняя формула получается из Формулы (11-10), если толщина пограничного слоя мала по сравнению с диаметром проволоки. Переходя к среднему значению коэффициента теплопередачи и вводя значение диаметра b / = 2. 5 x, можно увидеть следующее: Ню= 0. 400 (гр /⁴. Если отношение b / d мало, то знаменатель дроби ln (l-j-26 / d) равен «z. Поскольку он равен «b / d», то nud равен d / b. Таким образом, d / b = 0. 400 (grd) l/⁴, следовательно 1-11. ) Это решение очень хорошо согласуется с результатами эксперимента (l. 207).
Термодинамика заимствует понятия энергии и работы из других разделов физики, тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Людмила Фирмаль
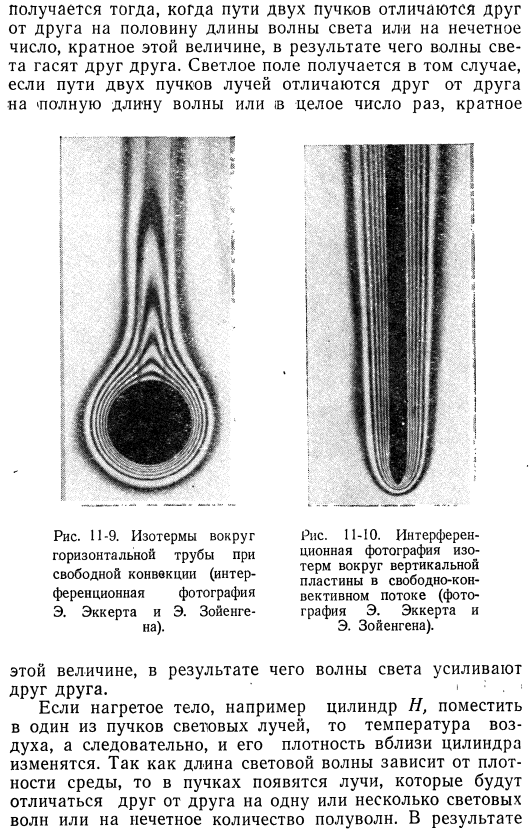
Пограничный слой и температурное поле можно легко наблюдать на фотографиях, сделанных с использованием оптических неоднородностей и интерференционных явлений среды. Метод использования оптической неоднородности среды очень прост, и Шмидт [l. 208]. Пример фотографии, сделанной таким образом, показан на рисунке. 11-7, показывает естественную конвекцию вокруг горизонтального цилиндра. Источник света, расположенный на большом расстоянии от нагреваемого цилиндра, обеспечивает изображение, показанное на фиг. 11-7, без средств изображения на экране, так что лучи проходят параллельно оси цилиндра. Лучи, проходящие через поле с градиентом плотности перпендикулярно направлению, отклоняются в сторону на определенный угол.
Таким образом, лучи, проходящие через нагретый пограничный слой, будут отклоняться СЫН ИЗ ЦИЛИНДРА. В результате, темная зона, соответствующая пограничном слое формируется вокруг ломаной линии (рис. 11-7). Э. Шмидт, расстояние от контура цилиндра до линии светлого сердца、 Рис. 11-7. Об определении толщины пограничного слоя методом естественной конвекции по фотографии, созданной с использованием неоднородности оптической среды и коэффициента теплоотдачи вокруг горизонтальной трубы[л. 370]. Рис. 11-8. Принципиальная схема КПС-де-ра-интерферометр Маха. Коэффициент теплопередачи. №.
Интерферометр Маха-Зендера (l. 2×9] принцип размещения показан на рис. 11-8. При прохождении через линзу конденсатора в световой пучок от монохроматического источника света а становится параллельным пучком. Таким образом, половина света отражается, а другая половина проходит через пластину. Часть отраженного света падает на зеркало d, а в конце его направляется на стеклянную пластину f, которая имеет те же характеристики, что и свет, прошедший через эту пластину. Пластина c. Эта часть Пластина проходит через пластину с и соединяется с лучами, отраженными от зеркала Е и пластины f.
Если 4 пластины c, d, e, f абсолютно параллельны, то лучи обоих лучей должны идти точно по одному и тому же пути. Затем на экране g, можно наблюдать темное или Яркое поле. Темное поле. Получается, что траектории двух лучей отличаются друг от друга на половину длины волны света или на нечетное число, кратное этому значению, в результате чего волны света гасят друг друга. Если путь двух лучей света отличается только»общей длиной волны»или» кратностью целого числа», получается яркое поле.
Диаграмма С-9. Изотермические линии вокруг горизонтальной трубы с естественной конвекцией (e. eckert и e. interference photos by zoengen). Рисунок 11-10. Интерферометрия Изотерм вокруг вертикальных пластин в условиях свободной конвекции (e. eckert and Э. Сойенген). Это величина, в результате которой световые волны усиливают друг друга. •:- Когда нагретый объект, например цилиндр h, помещается в один из лучей, температура воздуха, а следовательно, и плотность вблизи цилиндра, изменяется.
Поскольку длина волны света зависит от плотности среды, в ней появляется луч света. Лучи отличаются друг от друга только на 1 или более световых волн или нечетную половину waves. As итог На экране g вы увидите темные и светлые полосы вокруг тени цилиндра n. Вы можете увеличить резкость этих полос, поместив объектив между пластиной f и экраном. Это позволит создать изображение центральной плоскости цилиндра в плоскости экрана. Рисунки 11-9 и 11-10 представляют собой фотографии, сделанные описанным способом.
Фигура. 11-9 показаны фотографии естественной конвекции вокруг горизонтальной трубы. 11-10-фото естественной конвекции вдоль вертикальной пластины. Поскольку темные интерференционные полосы являются линиями постоянной плотности воздуха, а давление можно считать постоянным, эти полосы также являются изотермами. Температурный напор между любыми 2 соседними полосами можно легко рассчитать по длине цилиндра или пластины в направлении лучей, согласно интерферометру.
По фотографии можно определить градиент температуры воздуха на поверхности тела, а значит и коэффициент теплопередачи. Толщина пограничного слоя также очевидна, поэтому данный метод может быть с пользой использован при исследовании задач теплопередачи. Такой интерферометр впервые описали Цендер и Мах. Т. Цобель. 210] Р. Б. Кеннард. 211], e. eckert и e. zengen [l. 212] 3 исследования в области теплообмена. В рассмотренных примерах пограничные слои всегда были слоистыми.
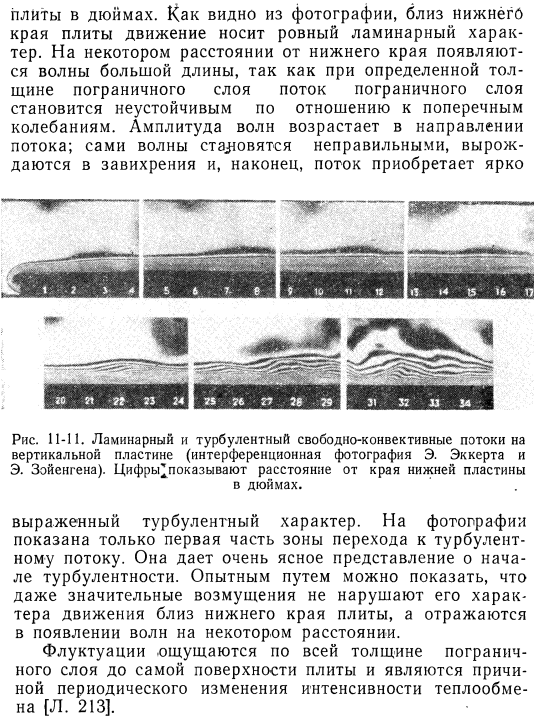
Пограничный слой, образующийся при свободной конвекции, также приобретает турбулентные характеристики, когда его толщина достигает определенной величины. Value. In воздух, (переход 6 ГД. = ’Возникает при некотором критическом значении критерия глашова порядка 1О⁹. Это соответствует критерию Рейнольдса rec = imax 6 / y = 550. Поэтому в условиях естественной конвекции переход из ламинарного состояния в турбулентное происходит при меньшем значении коэффициента Рейнольдса, чем при вынужденной конвекции conditions. In рис. (0.Обеспечивается, что пограничный слой становится турбулентным. Интерференционная линия — это изотермы.
Число указывает расстояние от нижнего края Плита из inches. As вы можете видеть на картинке, рядом с нижним краем пластины, движения по существу слоистые. При определенной толщине пограничного слоя течение пограничного слоя становится неустойчивым по отношению к боковым колебаниям, что приводит к появлению длинных волн на определенном расстоянии от нижней кромки. Амплитуда волны увеличивается в направлении течения. Сама волна становится нерегулярной и становится турбулентной, и, наконец, поток становится ярким Рисунок 11-11.
Естественная конвекция ламинарных и турбулентных потоков на вертикальной пластине (Э. Эккерт и Э. Интерференционные фотографии Зойенгена). Количество^указывает расстояние от края нижней пластины в дюймах. Выдающаяся турбулентность. На фото показана только первая часть переходной зоны к турбулентности. Дают очень четкое представление о начале турбулентности. Эмпирически показано, что даже серьезные возмущения не нарушают характер движения вблизи нижнего края пластины, а отражаются на появлении волн на определенном расстоянии. Колебания ощущаются от всей толщины пограничного слоя до поверхности пластины и являются причиной периодических изменений интенсивности теплопередачи[l. [213].
Смотрите также:
| Транспирация (просачивание через поры) и пленочное охлаждение | Турбулентный перенос тепла на вертикальной пластине |
| Свободная конвекция | Вывод уравнении пограничного слоя |

