




- Затем вы выводите общее дифференциальное уравнение в частных производных, которое можно использовать для нахождения распределения скоростей 2-мерного и 3-мерного потока. Отношения (7. 3) вязкое напряжение, определенное в этих уравнениях, играет важную роль. Однако, чтобы проиллюстрировать прямое применение определения вязкости в 1 важном простом случае, рассмотрим 1D стационарный ламинарный поток несжимаемой жидкости в горизонтальной кольцевой трубе с постоянным диаметром.
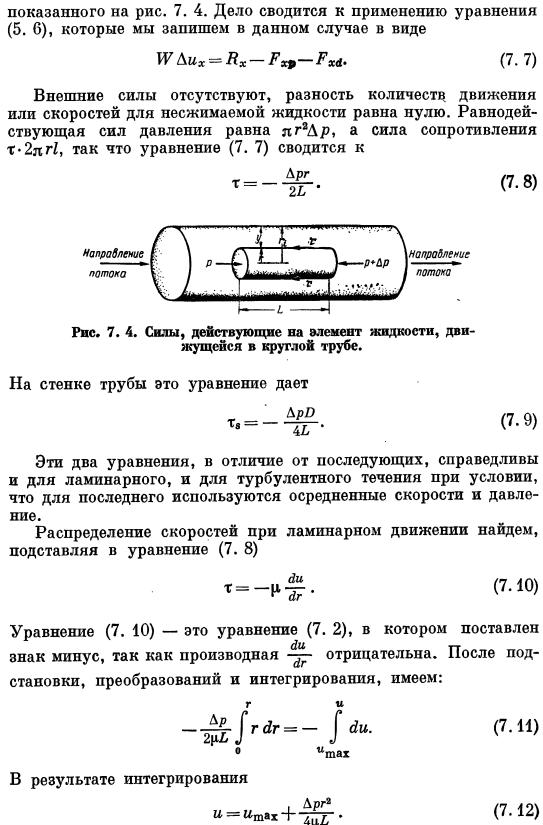
Найти распределение скорости и величину давления drop. To решив эту задачу, создадим уравнение равновесия для жидких элементов, показанное на рисунке. 7. 4.В данном случае имеет место уравнение(5. 6) приложение суммируется и записывается в следующем формате в случае ДАПП: RGDih = Ях-/х>-^. (7.7) Нет никакой внешней силы; разница в импульсе или скорости несжимаемой жидкости равна нулю. Поскольку результирующая сила давления равна dg2Dr, а сопротивление-t * 2lg1, уравнение (7. 7) быть Рисунок 7.
Сила, действующая на элемент движущейся жидкости в круглой трубе. В стенке трубы это уравнение имеет вид СРБ (7-9 )) Эти 2 уравнения, в отличие от последующих, справедливы как для ламинарных, так и для турбулентных течений. Однако последний использует среднюю скорость и давление. Формула (7. 8) найти распределение скоростей в движении ламинарного потока путем подстановки. (7.10)) Уравнение (7. 10) является уравнением(7. 2) поскольку дифференциал отрицательный, ставится знак минус. После замены, преобразования и интеграции вы можете: 0 itah В результате интеграции Мне Арг2 И-Ыщах + / «Г• (7.12) потому что u = 0 для r = r » в предположении, что на стене нет проскальзывания、 ДРГ?
И так оно и есть. Я =Мат•(7.14) Формула (7. 14) представляет собой параболическое распределение скорости. Уже использованный в Примере 3.1, ламинарный u = 4. 1, удельная энергия кипения равна b в уравнении энергетического баланса. если принять во внимание um = 2i6, то формула(7. 13)может быть записан в следующем формате: Д N = 8 ^ 1В = ВВ Р г? Это формула Хагена поасуйля, которая представляет собой падение давления устойчивого ламинарного потока в горизонтальной круглой трубе с постоянной площадью поперечного сечения. Из равновесия баланса механической энергии (4.27) следует ламинарный поток (Be (7.15 )) =(7-16) Формула потери на трение 7.
- Был выведен для горизонтальных труб, но для вертикальных труб тот же результат дает тот же вывод. Если профиль скорости трубы не зависит от направления трубы, то формула/ g / остается неизменной. Пример 7.1. Для того чтобы нагнести 57 l, пожалуйста высчитайте расход энергии и давление насос должен превратиться на эффективности 70%!Из сосуда под атмосферным давлением в резервуар при 20°С подается минимум 98% серной кислоты, по трубопроводу под избыточным давлением длиной 300 м, диаметром 52 мм, при 0,7 АТС уровень нижнего резервуара на 3 м выше уровня.
Формула (7. 16) вычислите среднюю скорость и число Рейнольдса, которое будет надежно применяться. 57•10-3 60-0. 785-5 22-10 дней = 0,45 м / с Относительная плотность 98%серной кислоты составляет 1,836 (185 в справочнике Перри), а вязкость-26,0 СПС(там же, стр. 372-373)… ПЛ 52-10 ″ 3.0, 45.1, 836-1000 Быть= ———- 2YYSY————- 165°-ламинарное течение, отсюда формула 7.
Требуемая мощность рассчитывается по формуле (4. 27). Кинетическая энергия и потери из-за расширения и сжатия потока в задаче ламинарного движения незначительны. Присвоение номеров является Lf = −128 Дж / кг Требуемая мощность при расходе 1,72 кг составляет секунды Увеличение давления на насосе определяется по формуле И макияж. Dr = _ 1,836 = 1 ′ 68 кг1см K Пример 7.2. Найдена зависимость скорости от расстояния от оси установившегося ламинарного движения неньютоновской жидкости в кольцевой трубе.
Зависимость напряжения от скорости сдвига имеет вид、 (1) Требуемый в этом случае знак минус отличается от выражения (7.4). Подставляя (1), выражение(7. Восемь) (2) Один Полномочия обеих сторон этого уравнения. После преобразования У нас есть: И затем т. О Ита (3) (____ До 2 кб) При запуске интеграции、 р _ (н + 1)/ н- | (4)и так как u = 0 для r = r、 у = umxx[1-(^)、+、)/]]。 (5) Формула 7.
Для сравнения этот результат показывает, что ламинарные профили скоростей неестественных флюидов могут существенно отличаться от профилей ньютоновских флюидов. Для псевдопластической жидкости получен относительно однородный профиль, а для ограниченного (n = 0) случая идеального пластического тела получено точное равномерное распределение скоростей. Для дилатантных жидкостей профиль является более протяженным, и в случае бесконечных пределов дилатантной жидкости (n = oo) скорость является линейной функцией радиуса, а профиль скорости-конусом.
Смотрите также:
| Вязкость Ньютоновских жидкостей | Потоки импульса, количества движения, массы и энергии |
| Реология неньютоновских жидкостей | Линии тока и функция тока |
