Оглавление:




Ламинарное изотермическое равномерное движение жидкости в плоской щели
Ламинарное изотермическое равномерное движение жидкости в плоской щели. Рассмотрим равномерное движение слоев. Часть потока жидкости w показана на фиг. 1 2-8 и да Форма показана на фиг. 12-9. To в какой-то степени. Слон находится в верхней половине. Трещины. Создайте уравнение движения для этого слоя. X}в плоскости, параллельной плоскости 2. Которые равномерно распределены рассматриваемыми частицами являются Перемещение слоев: равномерно, затем сумма проекций всех действий Сила, действующая на него по любой оси, должна быть равна нулю.
Смотрите также:
Это предположение справедливо только для бесконечно широких щелей. По сравнению с его толщиной. § 12-5] равномерное движение жидкости в плоской щели] 9b П 1. 1 1° — И фигура тоже. 12 * 8. Распределение скоростей Рост плоскощелевой ламы Поток наркотических веществ. И фигура тоже. 12-9. Силовая схема Над жидкостными плоскими элементами Ламинарного потока НТИ. » Посмотрим, какие силы проецируются на ось движения^ Предположим, что движущаяся ось горизонтальна. Это: Следующая власть.
Смотрите также:
По мере возрастания нестабильности внутреннее трение (вязкость) и поверхностное натяжение уменьшаются. Людмила Фирмаль
Сумма проекций этих сил на ось движения Ноль, т. е. : дуплексный. Да. Осадок, связанный с формулой (2-19) (12-31 потому что m и u являются функциями только r Последнее уравнение можно представить следующим образом: г Шри Если мы интегрируем уравнение (12-31) 2 раза, то получим: И^ — * + СГ — -. Константа интегрирования определяется из следующих условий 2-стейк при 0 и r = / g (Рис. 1 2-8), » = 0, whice 0 = 0」 И 2? * Подобный этому / И о о о о 1 9 2 ламинарное течение[гл. 12. Из этого уравнения видно, что скорость распределена. Парабола (Рис. 1 2-8).
Смотрите также:
Плоский радиальный ламинарный поток.
Найти среднюю скорость n для выражения «2-z4 в аренду> Гидравлический градиент равен следующему: (12-35 Удельные потери энергии рассчитываются по формуле А= А=^, (12-36 /- Длина щели (направление оси x). Очень часто используется также Формула (12-33) — (12-36 Расчет кольцевых щелей. Это не всегда приемлемое «но». Если ширина канала конечна, формула имеет вид <В этом случае уже невозможно учесть распределение скорости в плоскости. параллельно плоскости x, g, то же самое).
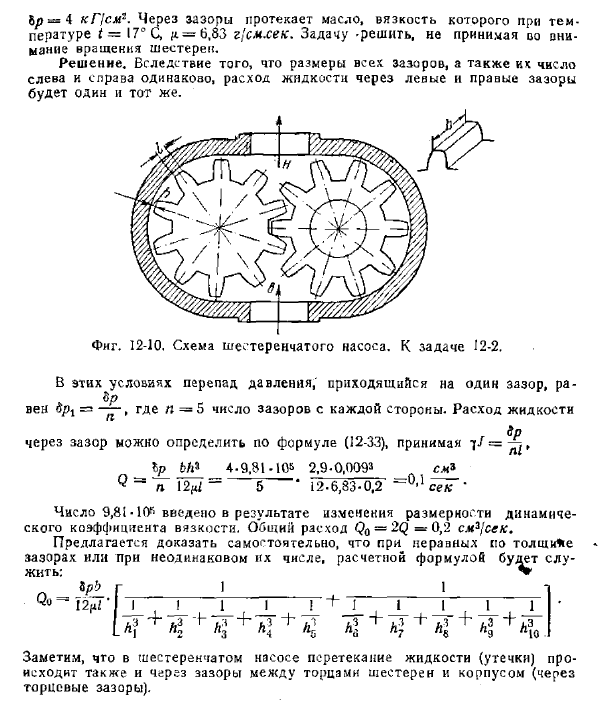
Значение пункта 2 в скобках формулы (12-37) — (12-39) невелико (12-33 (12’34 (12-36 перейдите на вкладку „Настройки“. В Формуле (1237) — (12 ^ 39), w обозначает гиперболический тангенс. Много В этих случаях достаточно ограничить их только значением n = 1. Задак 12-2. Из-за разницы в шестеренном насосе (рис. 12-10) Нагнетательная полость (n) и давление, создаваемое при всасывании Полость (e), часть жидкости из радиального зазора (l) Всасывание обратно в полость притяжения.
В то же время каждый слой имеет в общем случае различную скорость продольного движения. Людмила Фирмаль
- Количество вытекающей жидкости (утечка) по следующим данным : 1) каждый зазор представляет собой узкий зазор, его высота составляет h=: 0. 009 см Длина щели/ = 0, 2 см, ширина b =%9 см; 2) полная потеря давления § 12 * 6}плоский радиальный ламинарный поток 193 §^ ^ 4 кг / см2, масло течет через зазор, его вязкость Температура*-17°С, ^ = 6. 33 г! См, вторая задача-решить без рассмотрения Мания вращения шестерни. Решение, размеры всех зазоров и их количество Подача жидкости через зазор левого и правого Это будет то же самое.
И фигура тоже. 12-10. Шестеренный насос circuit. To выпуск 12-2. В этих условиях падение давления на зазор составляет ВР. Вена # 01= — — — -. Где n = 5-количество зон для каждого камня. Поток жидкости Число 9. 81 (p было введено в результате изменения размера Коэффициент вязкости. Полный поток φ0= 2 <3 = 0. 2 s l 3 / s » ag. Предлагается самостоятельно доказать, что толщина не равна В насосе с зубчатой передачей, обратите внимание жидкостное переполнение. Торцевой зазор.

