Оглавление:
Квадратные неравенства
Неравенства вида
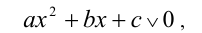
где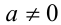 
, 
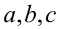— действительные числа или выражения, зависящие от параметров, а знак 
заменяет любой из знаков неравенств 
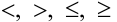или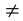 
, называются квадратными.
Если в квадратном неравенстве коэффициент b = 0 , то имеем
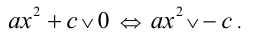
В случае а > 0 делением обеих частей на а получаем равносильное неравенство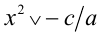 
(знак неравенства сохраняется). В случае а < 0 знак неравенства при делении на а изменится на противопо-ложный (см. пример 9 ниже). Обозначим 
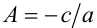. Тогда если 
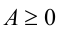, то
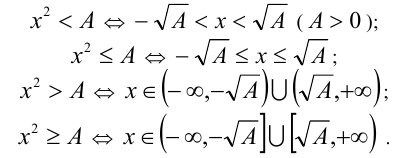
При А < 0 имеем
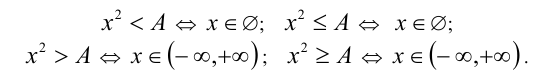
Рассмотрим теперь решение квадратных неравенств в случае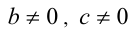 
, на примере неравенства
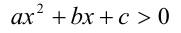
(решение неравенств вида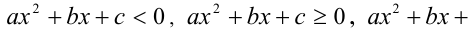 
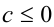, а также 
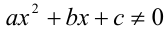рассмотрите самостоятельно). Воспользуемся при этом графиком квадратного трёхчлена.
Относительно знака старшего коэффициента возможны два случая.
1.Случай а > 0 :
а) есл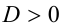и 
и 
,
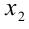, — корни квадратного трёхчлена, то решением неравенства будет объединение промежутков 
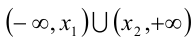(см. соответствующий график внизу на рисунке):
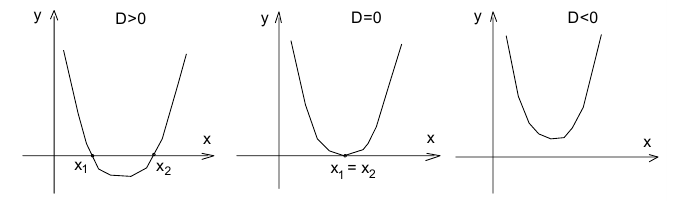
б) если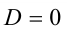 
, то решением неравенства будет вся числовая прямая, за исключением точки 
, т.е.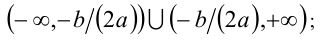 
в) если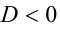 
, то неравенство верно при всех действительных x .
2.Случай а < 0:
а) если 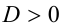, то решением неравенства будет интервал (, 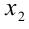); б) если 
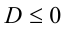, то неравенство не имеет решений (постройте иллюстрирующие графики и проанализируйте их самостоятельно).
Обратимся к решению последнего вида неравенств:
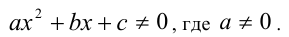
а) Если 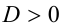, то решением неравенства будет объединение промежутков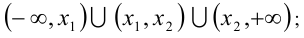 
б) если 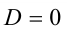, то неравенство выполнено при всех x , кроме 
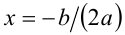, т.е. решением будет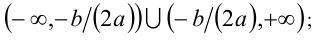 
в) если 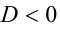, то неравенство справедливо сразу при всех действительных x .
Замечание. В случае 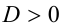квадратное неравенство можно также решать, не используя графический подход, а, найдя корни и представив неравенство в виде
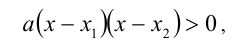
далее воспользоваться методом интервалов. В случае 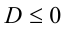неравенство решается при помощи очевидных оценок (методом оценок).
Пример №162.
Найти все значения параметра а , при которых трёхчлен
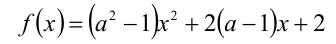
положителен при всех x.
Решение:
Во-первых, в условии задачи не говорится о квадратном трёхчлене, значит надо рассмотреть два случая, когда старший коэффициент равен или не равен нулю.
1) Пусть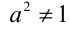 
, тогда для выполнения условия задачи необходимо и достаточно, чтобы
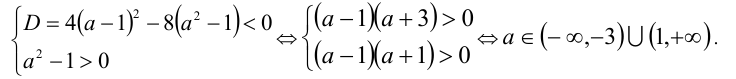
2) Если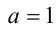 
, то трёхчлен принимает вид 
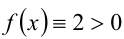при всех 
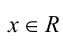, т.е. условие задачи выполняется.
3) Если же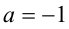 
, то имеем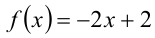 
, и это выражение не будет положительно сразу при всех 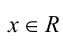, т.е. условие задачи не выполняется.
Ответ: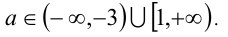
Пример №163.
Для каждой пары чисел а и b найти все решения неравенства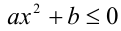 
.
Решение:
Перепишем данное неравенство в виде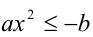 
.
1) Если а > 0 , то в результате деления на а неравенство приводится к виду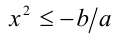 
.Очевидно, что в этом случае оно имеет решения только при 
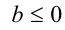. Итак, при 
, 
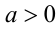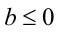имеем: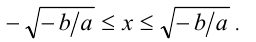 
2) Если а < 0, то поделим на а и придём к неравенству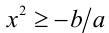 
. При b > 0 имеем решения 
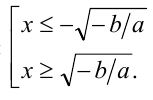При 
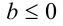имеем .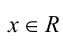
3) Если а = 0 , то неравенство принимает вид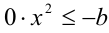 
. Очевидно, что тогда при 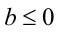имеем 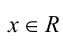, а при b > 0 нет решений.
Ответ: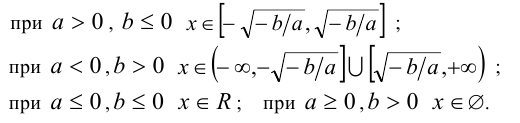 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
