Оглавление:
Сначала идёт теория, а потом готовые курсовые работы с подробным решением.
Теоретическая механика
Теоретическая механика – наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.
Статика
Плоская система сил
Статика — раздел теоретической механики, в котором изучаются методы приведения систем сил к простейшему виду и выводятся условия равновесия сил, приложенных к абсолютно твердому телу.
Основные задачи статики.
- Задача приведения системы сил: замена данной системы сил другой, более простой, ей эквивалентной.
- Задача о равновесии: изучаются условия равновесия тел под действием различных систем сил и определяются неизвестные реакции.
Основной мерой механического взаимодействия тел является сила.
Действие силы на любое тело определяется:
а) точкой приложения;
б) численной величиной или модулем силы;
в) линией действия;
г) направлением силы вдоль линии действия.
В системе СИ сила измеряется в Ньютонах. Сила через проекции её на координатные оси определяется следующим равенством
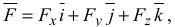
где 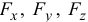 — проекции силы на оси координат;
— проекции силы на оси координат;
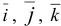 — орты этих осей.
— орты этих осей.
Возможно эта страница вам будет полезна:
| Предмет теоретическая механика |
Основные системы сил
- Система сходящихся сил на плоскости и в пространстве.
- Произвольная плоская система сил.
- Произвольная пространственная система сил.
Аксиомы статики
Аксиома 1. Если на твердое тело не действуют никакие силы, то оно находится в покое или совершает равномерное прямолинейное движение. Такое движение тела называется движением по инерции. Под равновесием тела понимается не только состояние покоя, но и движение его по инерции.
Вращение тела вокруг неподвижной оси с постоянной угловой скоростью есть частный случай его равновесия.
Аксиома 2. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны. Такие силы называются уравновешивающимися.
Аксиома 3. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил.
Системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.
Равнодействующей называется сила, которая эквивалентна данной системе сил.
Аксиома 4. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и определяется диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 1.1)
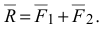
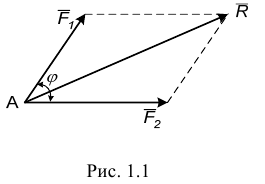
Модуль равнодействующей силы определяется по формуле
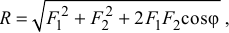
где 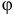 — угол между силами
— угол между силами 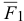 и
и 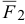 .
.
Аксиома 5. Два тела действуют друг на друга с силами, равными по величине и направленными по одной прямой в противоположные стороны.
Аксиома 6. Равновесие нетвердого тела не нарушается при его затвердевании.
Все вышеперечисленные аксиомы справедливы для свободных тел, перемещения которых в пространстве ничем не ограничиваются. В практике большей частью встречаются несвободные тела, перемещение которых в каких-то направлениях чем-либо ограничиваются. Все то, что ограничивает перемещения тел, называется связями. Так, для лампочки, подвешенной на проводе, связью является провод, для книги, лежащей на столе, связью будет стол и т. п.
Действие связи на тело характеризуется силами, которые называются реакциями связей.
Все силы, действующие на твердое тело, разделяют на активные силы и реакции связей. При этом активными называют силы, которые не являются реакциями связей. Активные силы часто называют задаваемыми, т. к. они, как правило, задаются условиями задач.
Аксиома 7. Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие на тело соответствующими реакциями связей.
Плоская система сил. Связи и реакции
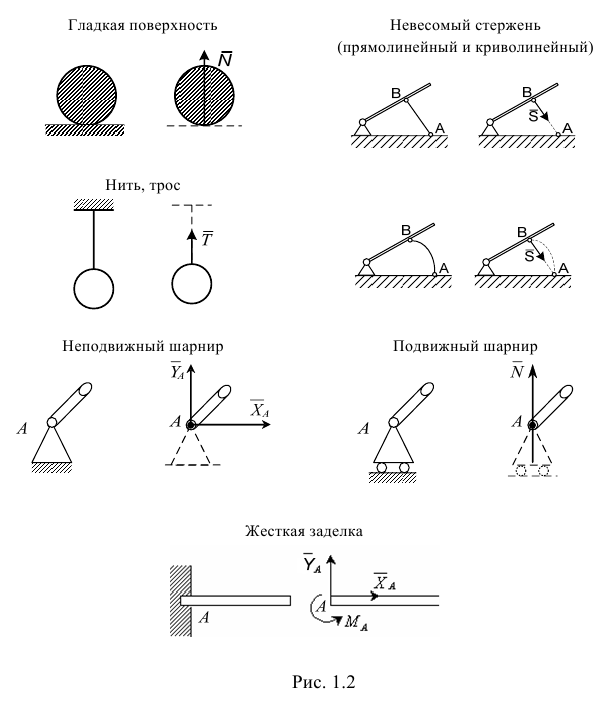
Если твердое тело соприкасается с другими телами, которые тем или иным образом ограничивают свободу его перемещения, то такие тела по отношению к рассматриваемому называются связями, а само рассматриваемое тело называется несвободным. Действие связей на несвободные тела характеризуется силами, которые называются реакциями связей. Основные их виды представлены на рис. 1.2.
Проекция сил на ось
Проекция вектора силы на ось — алгебраическая величина, равная произведению модуля силы на косинус угла между направлением силы и положительным направлением оси (рис. 1.3).

- Проекция положительна, если
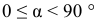 .
. - Проекция отрицательна, если
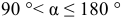 .
. - Проекция равна нулю, если
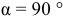 .
.
Момент силы относительно точки
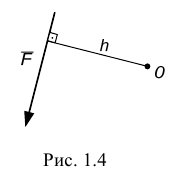
Момент силы 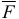 относительно точки 0 для плоской системы сил — это алгебраическая величина, равная произведению модуля силы
относительно точки 0 для плоской системы сил — это алгебраическая величина, равная произведению модуля силы 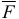 на кратчайшее расстояние
на кратчайшее расстояние 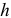 от точки 0 до линии действия силы
от точки 0 до линии действия силы 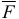 , которое называется плечом силы (рис. 1.4).
, которое называется плечом силы (рис. 1.4).
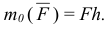
Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, при этом  .
.
Если сила 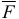 стремится повернуть тело вокруг точки 0 против хода часовой стрелки, то момент силы положительный, если же по ходу часовой стрелки, то момент силы отрицательный.
стремится повернуть тело вокруг точки 0 против хода часовой стрелки, то момент силы положительный, если же по ходу часовой стрелки, то момент силы отрицательный.
Пара сил
Система двух равных по модулю параллельных и противоположно направленных сил 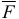 и
и 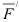 называется парой сил (рис. 1.5). Момент пары сил — это алгебраическая величина, равная произведению модуля одной из сил пары на кратчайшее расстояние между линиями действия сил
называется парой сил (рис. 1.5). Момент пары сил — это алгебраическая величина, равная произведению модуля одной из сил пары на кратчайшее расстояние между линиями действия сил 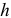 , которое называется плечом
, которое называется плечом
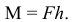
Момент пары сил положительный, если она стремится повернуть тело против хода часовой стрелки, и отрицательный, если по ходу часовой стрелки.
Свойства пары сил
- Алгебраическая сумма проекций пары сил на любую ось равна нулю.
- Алгебраическая сумма моментов сил, составляющих пару относительно произвольной точки плоскости, не зависит от выбора этой точки и равна моменту пары.
Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в ка-кой-либо его точке, такие силы называют сосредоточенными.
В действительности обычно силы бывают приложены к какой-либо части объема тела или его поверхности, а иногда к некоторой части линии. Такую нагрузку называют распределенной. Она характеризуется интенсивностью 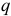 (рис. 1.6, 1.7).
(рис. 1.6, 1.7).
При решении задач распределенную нагрузку заменяют сосредоточенной силой — равнодействующей 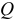 .
.
а) Равномерно распределенная нагрузка (рис. 1.6).
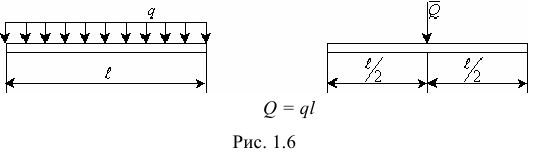
б) Распределенная нагрузка, изменяющаяся по линейному закону (рис. 1.7).
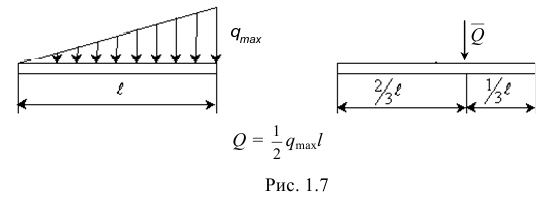
Приведение произвольной плоской системы сил к центру
В результате приведения сил, произвольно расположенных на плоскости, к центру 0 система сил преобразуется к приложенной в этом центре
силе, равной главному вектору 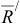 и паре сил, момент которой равен главному моменту
и паре сил, момент которой равен главному моменту 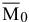 системы сил относительно центра приведения.
системы сил относительно центра приведения.
Используя метод проекций, можно вычислить модуль главного вектора:
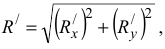
где
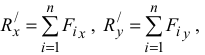
тогда
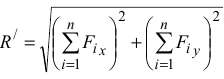
и определить его направление по направляющим косинусам
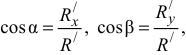
где 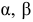 — углы между
— углы между 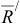 и положительными направлениями осей
и положительными направлениями осей 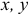 .
.
Главный момент системы сил относительно центра приведения равен алгебраической сумме моментов сил относительно центра приведения
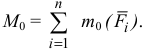
Уравнения равновесия системы сил, произвольно расположенных на плоскости
Условиями равновесия системы сил, произвольно расположенных на плоскости, являются равенство нулю главного вектора и главного момента:

В скалярной форме эти условия запишутся в виде уравнений
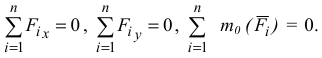
Эти условия называются уравнениями равновесия произвольной плоской системы сил.
Готовые курсовые работы:
- Курсовая работа С1 Жесткая рама имеет в точке неподвижный шарнир, а в точке шарнирно-подвижную опору. На раму действуют распределенная нагрузка интенсивности , пара сил с моментом , сосредоточенные силы . При расчете принять .
- Курсовая работа С2 На угольник , конец которого жестко заделан в точке , опирается стержень . Стержень в точке имеет шарнирную опору. На угольник действует пара сил с моментом . К стержню приложена горизонтальная сила , на участке действует равномерно распределенная нагрузка интенсивностью (прил. 2, рис. С 2).
Пространственная система сил
Пространственная система сходящихся сил приводится к равнодействующей 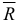 , которая равна
, которая равна 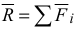 . Модуль равнодействующей
. Модуль равнодействующей 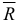 равен
равен 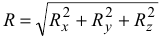 . Направляющие косинусы определяются по формулам
. Направляющие косинусы определяются по формулам
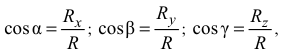
где 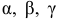 — углы между направлением
— углы между направлением 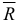 и положительными направлениями осей
и положительными направлениями осей 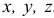 . Для равновесия твердого тела, к которому приложена пространственная система сходящихся сил, необходимо, чтобы равнодействующая равнялась нулю:
. Для равновесия твердого тела, к которому приложена пространственная система сходящихся сил, необходимо, чтобы равнодействующая равнялась нулю: 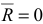 . При этом уравнения равновесия имеют вид
. При этом уравнения равновесия имеют вид
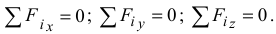
Проекции силы на плоскость и на ось (метод двойного проектирования)
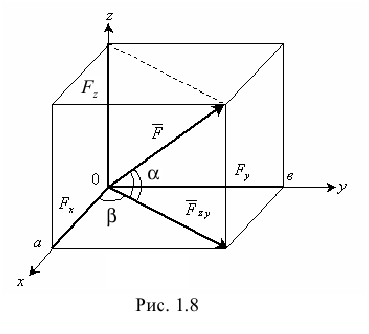
При определении проекции силы на координатную ось, когда неизвестен угол между осью и линией действия силы, используют метод двойного проектирования. Вначале находят проекцию 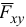 силы
силы 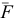 (рис. 1.8) на координатную плоскость
(рис. 1.8) на координатную плоскость 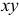 , а затем вычисляют проекцию вектора
, а затем вычисляют проекцию вектора 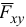 на ось
на ось 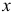 или
или 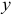 :
:
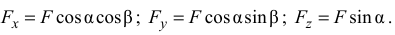
Нужно помнить, что проекция силы на ось является алгебраической величиной, проекция силы на плоскость есть вектор.
Произвольная пространственная система сил
Произвольная пространственная системы сил приводится к главному вектору 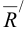 и главному моменту
и главному моменту 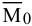 . Модуль главного вектора определяется по формуле:
. Модуль главного вектора определяется по формуле:
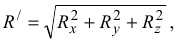
где
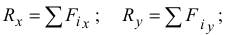
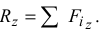
Модуль главного момента
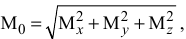
где

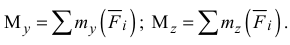
Момент силы относительно оси
Момент силы относительно оси 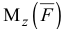 (рис. 1.9) определяется как алгебраическая величина, равная произведению модуля проекции силы
(рис. 1.9) определяется как алгебраическая величина, равная произведению модуля проекции силы 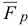 на плоскость
на плоскость 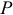 , перпендикулярную к оси
, перпендикулярную к оси 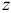 , на кратчайшее расстояние
, на кратчайшее расстояние 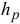 от точки 0 пересечения оси с этой плоскостью до линии действия проекции силы на плоскость
от точки 0 пересечения оси с этой плоскостью до линии действия проекции силы на плоскость 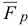 , то есть
, то есть
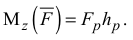
Если с конца оси 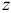 видно, что сила
видно, что сила 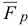 стремится повернуть тело вокруг точки 0 против часовой стрелки, то момент положительный, если по часовой стрелке, то отрицательный, то есть
стремится повернуть тело вокруг точки 0 против часовой стрелки, то момент положительный, если по часовой стрелке, то отрицательный, то есть
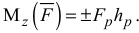
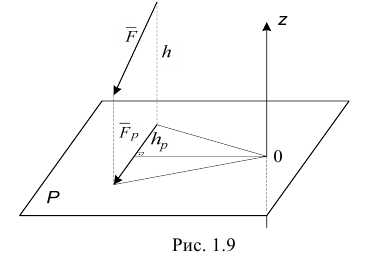
Момент силы относительно оси равен нулю, если линия действия силы параллельна оси или ее пересекает.
Условии и уравнении равновесии произвольной пространственной системы сил
Условиями равновесия произвольной пространственной системы сил являются равенство нулю главного вектора и главного момента, 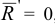 ,
, 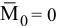 . Тогда получаем уравнения равновесия
. Тогда получаем уравнения равновесия

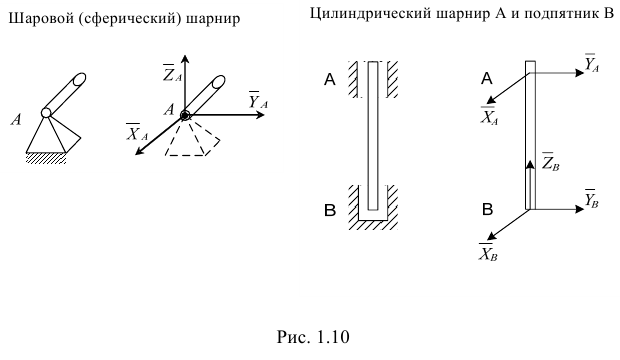
Связи и реакции в пространстве (рис. 1.10)
Готовые курсовые работы:
- Курсовая работа С 3 Конструкция состоит из невесомых стержней 1, 2…6, соединенных друг с другом (в узлах и ) и с неподвижными опорами шарнирами (прил. 3, рис. С 3).
- Курсовая работа С 3.1 Две однородные прямоугольные плиты жестко соединены под прямым углом и закреплены в точке сферическим шарниром, в точке — цилиндрическим шарниром и невесомым стержнем 1. Стержень соединен с плитой и опорой шарниром.
Кинематика
Кинематика точки
Кинематика — раздел теоретической механики, в котором изучаются механические движения материальных точек и тел с геометрической точки зрения вне зависимости от действующих на них сил.
При этом задаются математическим методом способы задания движения точек и тел и определяются по заданному закону движения все основные кинематические характеристики, такие как траектория точки, скорость и ускорение точки, угловые скорости и угловые ускорения тел.
При движении тела все его точки в общем случае совершают различное движение. Поэтому изучению движения тела предшествует изучение движения точки.
Непрерывную линию, которую описывает в пространстве точка при своем движении, называют траекторией точки. По виду траектории движение точки делится на прямолинейное и криволинейное.
Способы задании движении точки
- Векторный способ
Положение точки 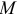 в любой момент времени определяется заданием радиус-вектора точки
в любой момент времени определяется заданием радиус-вектора точки 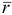 , начало которого помещается в некотором неподвижном центре, а конец совмещается с движущейся точкой. С течением времени вектор
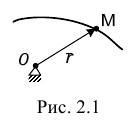
, начало которого помещается в некотором неподвижном центре, а конец совмещается с движущейся точкой. С течением времени вектор 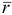 изменяется и по модулю, и по направлению (рис. 2.1)
изменяется и по модулю, и по направлению (рис. 2.1)
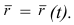
- Координатный способ
При рассмотрении движения в прямоугольной декартовой системе координат указанный способ заключается в задании координат 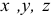 точки как известной функции времени (рис. 2.2)
точки как известной функции времени (рис. 2.2)
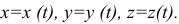
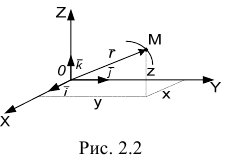
Связь между координатным и векторным способами задания движения осуществляется уравнением (см. рис. 2.2)
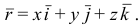
Например, радиус-вектор задан уравнением
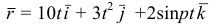
Это означает, что точка движется относительно координатных осей согласно уравнениям
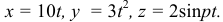
Из примера видно, что если движение точки задано в координатной форме, то при необходимости всегда можно перейти к векторному способу задания движения.
- Естественный способ
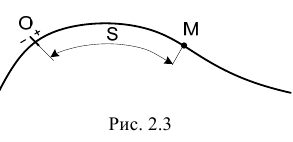
При естественном способе задания движения известна траектория точки, выбирается начало положительного и отрицательного отсчета криволинейной координаты и задается закон движения точки по траектории 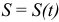 (рис. 2.3).
(рис. 2.3).
Определение скорости и ускорения точки
- Векторный способ
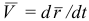 — вектор скорости точки в данный момент времени;
— вектор скорости точки в данный момент времени;
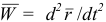 — вектор ускорения точки в данный момент времени.
— вектор ускорения точки в данный момент времени.
Вектор скорости 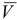 направлен по касательной к траектории в данной точке в сторону движения. Вектор ускорения
направлен по касательной к траектории в данной точке в сторону движения. Вектор ускорения 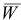 направлен в сторону вогнутости траектории (рис 2.4).
направлен в сторону вогнутости траектории (рис 2.4).
- Координатный способ
а)  — скорость точки.
— скорость точки.
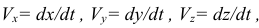
где 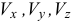 — проекции скорости на оси координат. Направление вектора определяется по направляющим косинусам
— проекции скорости на оси координат. Направление вектора определяется по направляющим косинусам
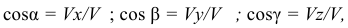
где 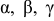 — углы, которые составляет вектор скорости точки с положительными направлениями осей
— углы, которые составляет вектор скорости точки с положительными направлениями осей 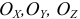 соответственно.
соответственно.
б) 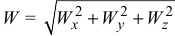 — ускорение точки.
— ускорение точки.
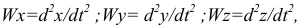
где 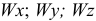 — проекции ускорения точки на оси координат.
— проекции ускорения точки на оси координат.
Направления определим по формулам
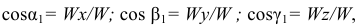
где 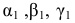 — углы, которые составляет вектор ускорения с положительными направлениями осей
— углы, которые составляет вектор ускорения с положительными направлениями осей 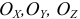 соответственно.
соответственно.
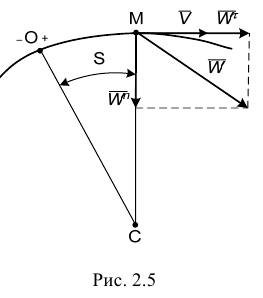
- Естественный способ (рис. 2.5).
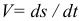 — скорость точки;
— скорость точки;
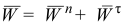 — вектор ускорения точки;
— вектор ускорения точки;
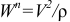 — нормальное ускорение точки;
— нормальное ускорение точки;
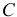 — центр кривизны;
— центр кривизны;
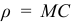 — радиус кривизны траектории;
— радиус кривизны траектории;
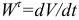 — касательное ускорение точки;
— касательное ускорение точки;
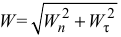 — модуль ускорения точки.
— модуль ускорения точки.
Возможно эта страница вам будет полезна:
| Решение задач по теоретической механике |
Готовая курсовая работа:
Кинематика плоского движения твердого тела
При изучении этого раздела надо уметь определять линейную скорость и полное ускорение точек твердого тела, совершающего вращение вокруг неподвижной оси (вращательное движение), с помощью угловых параметров вращения тела: угловой скорости 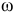 и углового ускорения
и углового ускорения 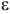 .
.
Угловая скорость 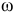 изображается круглой стрелкой вокруг оси и показывает направление вращения тела. При ускоренном вращении круглые стрелки угловой скорости
изображается круглой стрелкой вокруг оси и показывает направление вращения тела. При ускоренном вращении круглые стрелки угловой скорости 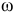 и углового ускорения
и углового ускорения 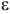 совпадают по направлению, а при замедленном — направлены противоположно.
совпадают по направлению, а при замедленном — направлены противоположно.
Траекторией движения точки является окружность, радиус которой 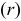 равен кратчайшему расстоянию от заданной точки до оси вращения тела (далее радиус вращения).
равен кратчайшему расстоянию от заданной точки до оси вращения тела (далее радиус вращения).
Модуль вектора линейной скорости определяется по формуле
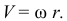
Вектор 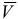 направлен по касательной к траектории или перпендикулярно радиусу вращения в направлении угловой скорости
направлен по касательной к траектории или перпендикулярно радиусу вращения в направлении угловой скорости 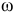 тела. Полное ускорение точки
тела. Полное ускорение точки
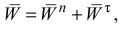
где 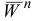 — нормальное ускорение точки;
— нормальное ускорение точки;
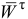 — касательное ускорение точки.
— касательное ускорение точки.
Модуль нормального ускорения точки
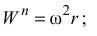
Вектор 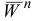 направлен от заданной точки по нормали к центру кривизны траектории (в данном случае по радиусу вращения) к оси вращения.
направлен от заданной точки по нормали к центру кривизны траектории (в данном случае по радиусу вращения) к оси вращения.
Модуль касательного ускорения точки
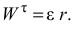
Вектор касательного ускорения точки 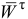 направлен перпендикулярно вектору нормального ускорения
направлен перпендикулярно вектору нормального ускорения 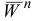 в сторону круглой стрелки углового ускорения
в сторону круглой стрелки углового ускорения 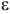 , т. е. вектор касательного ускорения
, т. е. вектор касательного ускорения 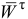 направлен по касательной к траектории или перпендикулярно радиусу вращения в ту же сторону, что и вектор скорости
направлен по касательной к траектории или перпендикулярно радиусу вращения в ту же сторону, что и вектор скорости 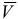 точки при ускоренном вращении, а при замедленном — в противоположную.
точки при ускоренном вращении, а при замедленном — в противоположную.
Модуль полного ускорения точки
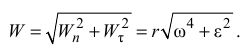
Плоскопараллельным движением (плоским) называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называемой плоскостью движения. При таком движении все точки, лежащие на линиях, перпендикулярных к плоскостям их движения, перемещаются по одинаковым траекториям и имеют одинаковые скорости и ускорения, т. к. эти линии при движении тела остаются параллельными самим себе.
Поэтому задача на изучение плоскопараллельного движения сводится к изучению плоского сечения (плоской фигуры), параллельного некоторой неподвижной плоскости.
Движение плоской фигуры в ее плоскости в каждый момент времени можно рассматривать состоящим из двух движений: поступательного движения плоской фигуры вместе с произвольной точкой, принятой за полюс, и вращательного вокруг полюса.
Планом скоростей называется диаграмма, на которой от некоторого центра в выбранном масштабе для данного момента времени отложены скорости точек плоской фигуры. При построении плана используется теорема о скоростях точек тела при плоскопараллельном движении
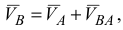
где 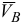 — искомая скорость;
— искомая скорость;
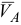 — известная скорость точки
— известная скорость точки 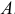 , выбираемой за полюс;
, выбираемой за полюс;
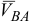 — вращательная скорость точки
— вращательная скорость точки 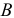 при повороте вокруг полюса
при повороте вокруг полюса 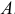 .
.
Вектор вращательной скорости 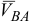 направляется перпендикулярно отрезку
направляется перпендикулярно отрезку 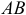 , соединяющему данную точку
, соединяющему данную точку 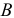 с полюсом
с полюсом 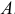 , в сторону вращения. Модуль вращательной скорости
, в сторону вращения. Модуль вращательной скорости
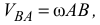
где 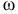 — мгновенная угловая скорость вращения плоской фигуры. Аналогично определяются скорости других точек.
— мгновенная угловая скорость вращения плоской фигуры. Аналогично определяются скорости других точек.
Подробное построение плана скоростей приведено далее в примере. Мгновенным центром скоростей называется точка 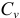 плоской фигуры, скорость которой в данный момент времени равна нулю, т. е.
плоской фигуры, скорость которой в данный момент времени равна нулю, т. е. 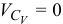 .
.
Если такая точка определена, то скорость любой точки плоской фигуры в данный момент времени равна вращательной скорости данной точки при вращении вокруг мгновенного центра скоростей
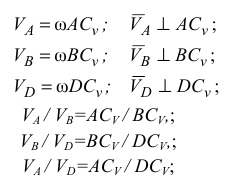
Таким образом, скорости всех точек плоской фигуры перпендикулярны отрезкам, соединяющим их с мгновенным центром скоростей, пропорциональны этим отрезкам и направлены в сторону угловой скорости вращения 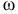 .
.
Рассмотрим некоторые случаи определения положения мгновенного центра скоростей.
1) Если известны линии действия векторов скоростей двух точек плоской фигуры, то мгновенный центр скоростей 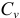 находится на пересечении перпендикуляров, восстановленных к скоростям этих точек (рис. 2.6).
находится на пересечении перпендикуляров, восстановленных к скоростям этих точек (рис. 2.6).
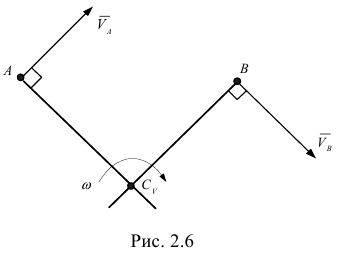
2) Следует иметь в виду, что если перпендикуляры, восстановленные к скоростям двух точек, не пересекаются, то 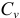 фигуры в данный момент времени расположен в бесконечности и она совершает мгновенно-поступательное движение, т. е.
фигуры в данный момент времени расположен в бесконечности и она совершает мгновенно-поступательное движение, т. е. 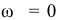 , а скорости всех точек геометрически равны
, а скорости всех точек геометрически равны
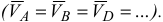
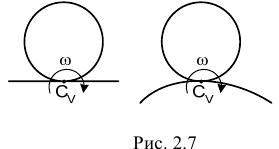
3) Тело катится без скольжения по неподвижной плоскости или поверхности. В этом случае мгновенный центр скоростей находится в точке касания тела с неподвижной плоскостью или поверхностью (рис. 2.7).
Согласно теореме об ускорениях точек плоской фигуры ускорение какой-либо её точки определяется формулой
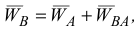
где 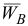 — искомое ускорение;
— искомое ускорение;
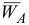 — известное ускорение точки
— известное ускорение точки 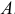 , принятой за плюс;
, принятой за плюс; 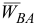 — ускорение точки
— ускорение точки 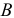 при вращении вокруг плюса
при вращении вокруг плюса 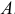 . Ускорение
. Ускорение 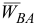 определяют по составляющим
определяют по составляющим
Так как
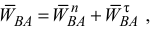
тогда
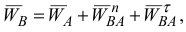
где  — нормальное ускорение точки
— нормальное ускорение точки 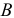 при вращении вокруг плюса
при вращении вокруг плюса 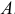 ;
; 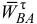 — касательное ускорение точки
— касательное ускорение точки 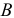 при вращении вокруг плюса
при вращении вокруг плюса 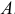 ;
;
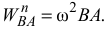
Вектор  направлен от точки
направлен от точки 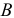 к плюсу
к плюсу 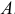 вдоль отрезка
вдоль отрезка 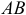
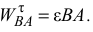
Вектор 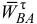 направлен перпендикулярно отрезку
направлен перпендикулярно отрезку 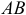 в сторону круглой стрелки углового ускорения
в сторону круглой стрелки углового ускорения 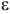 .
.
Модуль ускорения точки 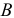 при вращении вокруг плюса
при вращении вокруг плюса 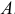
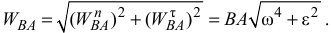
Воспользуемся другим способом определения ускорений точек при плоском движении твердого тела с помощью мгновенного центра ускорений.
Мгновенным центром ускорений называется точка 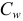 плоской фигуры, ускорение которой в данном положении равно нулю
плоской фигуры, ускорение которой в данном положении равно нулю 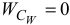 .
.
Если положение мгновенного центра ускорений известно, то ускорение любой точки плоской фигуры в данный момент времени определяется как ускорение этой точки при вращении фигуры вокруг мгновенного центра ускорений, т. е.
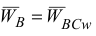
или
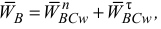
где 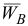 — искомое ускорение;
— искомое ускорение;
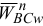 — нормальное ускорение точки
— нормальное ускорение точки 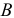 при вращении фигуры вокруг мгновенного центра ускорений
при вращении фигуры вокруг мгновенного центра ускорений 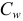 ;
;
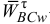 — касательное ускорение точки
— касательное ускорение точки 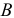 при вращении фигуры вокруг мгновенного центра ускорений
при вращении фигуры вокруг мгновенного центра ускорений 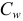
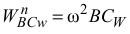
Вектор 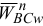 направлен от точки
направлен от точки 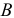 вдоль отрезка
вдоль отрезка  к мгновенному центру ускорений
к мгновенному центру ускорений 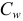
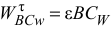
Вектор 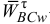 направлен перпендикулярно отрезку
направлен перпендикулярно отрезку  в сторону круглой стрелки углового ускорения
в сторону круглой стрелки углового ускорения 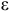
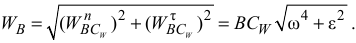
Ускорения точек плоской фигуры пропорциональны их расстояниям до мгновенного центра ускорений
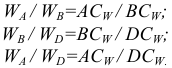
Для поиска положения мгновенного центра ускорений определяется угол между вектором полного ускорения точки плоской фигуры и отрезком, соединяющим данную точку с мгновенным центром ускорений 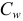 , по формуле
, по формуле
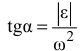
и расстояние от данной точки до мгновенного центра ускорений
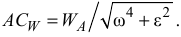
Методика определения положения мгновенного центра ускорений подробно рассматривается далее в примере.
Готовая курсовая работа:
Возможно эта страница вам будет полезна:
| Помощь по теоретической механике |
Сложное движение точки
Если движение точки изучается по отношению к двум системам координат, одна из которых неподвижна, а другая по отношению к первой движется определенным образом, то такое движение точки называется сложным, или составным.
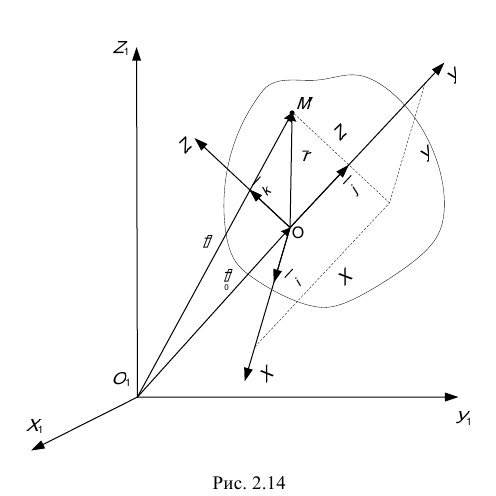
Пусть точка 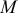 движется по некоторой кривой (рис. 2.14). Рассмотрим её движение по отношению к двум системам координат, неподвижной
движется по некоторой кривой (рис. 2.14). Рассмотрим её движение по отношению к двум системам координат, неподвижной 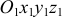 и подвижной
и подвижной 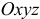 , которая движется по отношению к неподвижной.
, которая движется по отношению к неподвижной.
При сложном движении точки различают абсолютное, относительное и переносное движение.
Движение точки 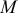 относительно неподвижной системы называется абсолютным движением.
относительно неподвижной системы называется абсолютным движением.
Движение точки 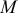 относительно подвижной системы называется относительным движением.
относительно подвижной системы называется относительным движением.
Движение точки 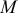 вместе с подвижной системой относительно неподвижной называется переносным движением. На рис. 2.14 покажем радиусы-векторы:
вместе с подвижной системой относительно неподвижной называется переносным движением. На рис. 2.14 покажем радиусы-векторы:
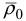 — радиус-вектор, определяющий положение начала координат
— радиус-вектор, определяющий положение начала координат 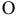 подвижной системы по отношению к неподвижной системе,
подвижной системы по отношению к неподвижной системе,
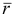 — радиус-вектор, определяющий положение точки
— радиус-вектор, определяющий положение точки 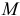 относительно подвижной системы,
относительно подвижной системы,
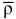 — радиус-вектор, определяющий положение точки
— радиус-вектор, определяющий положение точки 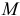 относительно неподвижной системы координат.
относительно неподвижной системы координат.
В процессе движения точки сохраняется следующая зависимость (см. рис. 2.14).
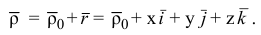
Определение скорости при сложном движении точки
Определяя относительную скорость 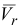 , мысленно останавливаем переносное движение. При этом векторы
, мысленно останавливаем переносное движение. При этом векторы  будут величинами постоянными. Тогда, дифференцируя по времени равенство (2.1), получим:
будут величинами постоянными. Тогда, дифференцируя по времени равенство (2.1), получим:
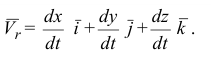
При определении переносной скорости 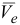 останавливается относительное движение. Это означает, что координаты относительного положения точки
останавливается относительное движение. Это означает, что координаты относительного положения точки 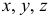 — величины постоянные. Продифференцируем по времени равенство (2.1),
— величины постоянные. Продифференцируем по времени равенство (2.1),
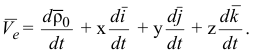
Если считать, что точка участвует одновременно в двух движениях, то, дифференцируя по времени равенство (2.1), найдем:
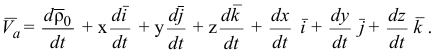
Сопоставляя равенства (2.2), (2.3) и (2.4), получаем:
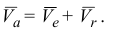
Равенство (2.5) называется формулой сложения скоростей при сложном движении точки.
Определение ускорения при сложном движении точки
Абсолютное ускорение точки определяется по формуле
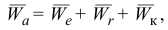
где 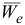 — переносное ускорение;
— переносное ускорение; 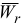 — относительное ускорение;
— относительное ускорение; 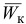 — ускорение Кориолиса.
— ускорение Кориолиса.
Равенство (2.6) выражает теорему Кориолиса. Вывод этой теоремы можно найти в учебниках по теоретической механике.
Вектор ускорения Кориолиса определяется по формуле
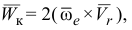
где 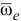 — вектор переносной угловой скорости точки;
— вектор переносной угловой скорости точки;
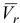 — вектор относительной скорости точки. Модуль ускорения Кориолиса определяется уравнением
— вектор относительной скорости точки. Модуль ускорения Кориолиса определяется уравнением
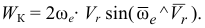
Направление вектора 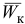 можно определить по правилу векторного произведения или по правилу Н. Е. Жуковского, согласно которому относительную скорость
можно определить по правилу векторного произведения или по правилу Н. Е. Жуковского, согласно которому относительную скорость 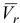 надо спроектировать на плоскость, перпендикулярную к оси переносного вращения, и повернуть эту проекцию в сторону переносного вращения на 90° (рис. 2.15). В случае поступательного переносного движения
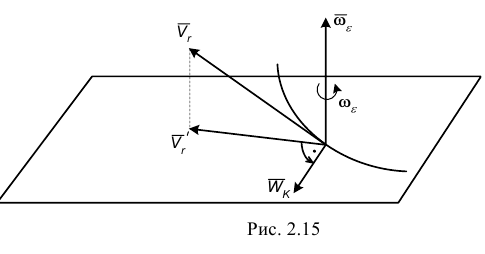
надо спроектировать на плоскость, перпендикулярную к оси переносного вращения, и повернуть эту проекцию в сторону переносного вращения на 90° (рис. 2.15). В случае поступательного переносного движения 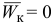 , так как
, так как 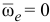 . Тогда формула (2.6) запишется
. Тогда формула (2.6) запишется
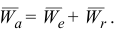
Готовая курсовая работа:
Возможно эта страница вам будет полезна:
| Заказать работу по теоретической механике |
Динамика
Динамика — раздел теоретической механики, в котором изучается движение материальных точек и тел в зависимости от действующих на них сил и их инерционности.
Основные законы динамики
- Закон инерции
Если на материальную точку не действуют никакие силы, то она находится в покое или совершает прямолинейное равномерное движение.
- Закон пропорциональности силы и ускорения (основной закон)
Ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление
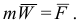
Если на точку действует несколько сил, то основной закон примет вид
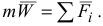
- Закон равенства действия и противодействия
Две точки или два тела действуют друг на друга с силами, равными по величине и направленными вдоль одной прямой в противоположные стороны.
- Закон независимости действия сил
Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.
Системы отсчета, в которых выполняются первый и второй законы, называются инерциальными, в противном случае их называют неинерциальными.
Третий закон динамики выполняется при рассмотрении движения тел в любых системах отсчета.
Динамика материальной точки
Дифференциальные уравнения движения материальной точки в декартовых координатах
Основное уравнение динамики имеет вид
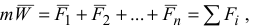
где 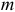 — масса точки;
— масса точки;
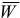 — ускорение точки;
— ускорение точки;
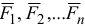 — силы, действующие на точку (учитываются как активные силы, так и реакции связей, если точка несвободная).
— силы, действующие на точку (учитываются как активные силы, так и реакции связей, если точка несвободная).
Проектируя обе части векторного равенства (3.1) на координатные оси, получим:
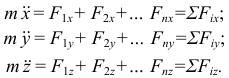
Уравнения (3.2) называются дифференциальными уравнениями движения материальной точки; здесь 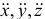 — проекции ускорения точки на оси декартовой системы координат;
— проекции ускорения точки на оси декартовой системы координат;
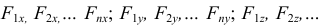
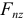 — проекции сил на оси декартовой системы координат.
— проекции сил на оси декартовой системы координат.
Задачи динамики точки
В динамике точки рассматриваются две основные задачи. Их решение приведем на примере использования декартовой системы координат.
Первая задача динамики
По заданной массе точки 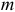 и уравнениям ее движения
и уравнениям ее движения
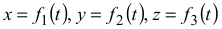
требуется определить модуль и направление равнодействующей сил, приложенных к точке.
Из дифференциальных уравнений (3.2) проекции равнодействующей на координатные оси определяются равенствами
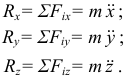
Масса точки 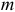 задана, надо знать
задана, надо знать 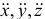 . Для их определения следует дважды продифференцировать по времени заданные уравнения движения точки. Затем, зная
. Для их определения следует дважды продифференцировать по времени заданные уравнения движения точки. Затем, зная 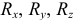 , определяют модуль равнодействующей по формуле
, определяют модуль равнодействующей по формуле 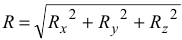 и направление по направляющим косинусам
и направление по направляющим косинусам
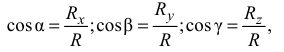
где 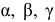 — углы между направлением равнодействующей
— углы между направлением равнодействующей 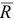 и положительным направлением осей
и положительным направлением осей 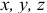 соответственно.
соответственно.
Вторая задача динамики
Зная силы, действующие на материальную точку, ее массу 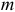 , а также начальные условия движения (начальное положение точки и ее начальную скорость), получить уравнения движения точки.
, а также начальные условия движения (начальное положение точки и ее начальную скорость), получить уравнения движения точки.
Для решения этой задачи необходимо в левую часть дифференциальных уравнений (3.3) подставить значение массы 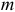 , а в правую часть -суммы проекций приложенных сил и полученные уравнения дважды проинтегрировать по времени, а затем по начальным условиям определить постоянные интегрирования
, а в правую часть -суммы проекций приложенных сил и полученные уравнения дважды проинтегрировать по времени, а затем по начальным условиям определить постоянные интегрирования 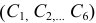 .
.
Готовая курсовая работа:
Общие теоремы динамики
Теорема о движении центра масс механической системы
Под механической системой понимается совокупность материальных точек, положение и движение которых взаимосвязаны. Например, движение коленчатого вала двигателя внутреннего сгорания зависит от движения его поршней; движение планет солнечной системы обусловлено силами их взаимного притяжения и т. д.
При изучении движения механических систем силы разделяют на внешние 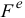 и внутренние
и внутренние 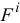 .
.
Внешними называются силы, с которыми действуют на точки и тела рассматриваемой системы точки и тела, не входящие в состав этой системы. Внутренними называются силы, с которыми точки и тела рассматриваемой системы действуют друг на друга.
Положение центра масс системы, точки 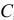 , определяется равенством
, определяется равенством
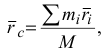
где 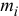 — масса отдельной точки системы;
— масса отдельной точки системы;
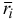 — радиус-вектор, определяющий положение этой точки системы;
— радиус-вектор, определяющий положение этой точки системы; 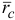 — радиус-вектор, определяющий положение центра масс системы;
— радиус-вектор, определяющий положение центра масс системы; 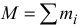 — масса системы. Для
— масса системы. Для 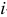 -й точки запишем основной закон динамики
-й точки запишем основной закон динамики
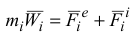
или
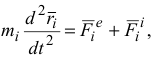
где нижний индекс
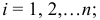
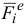 — равнодействующая приложенных к точке внешних сил;
— равнодействующая приложенных к точке внешних сил;
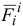 — равнодействующая приложенных к точке внутренних сил.
— равнодействующая приложенных к точке внутренних сил.
Суммируя уравнения (3.5), получим:
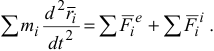
Продифференцируем дважды по времени уравнение (3.4).
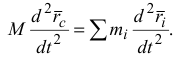
Тогда, учитывая полученное выражение и то, что 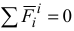 (свойство внутренних сил), уравнение (3.6) запишется:
(свойство внутренних сил), уравнение (3.6) запишется:
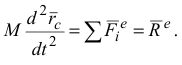
Зная, что
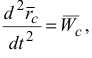
получаем:
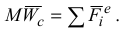
Уравнение (3.7) выражает теорему о движении центра масс механической системы.
Центр масс механической системы движется как материальная точка массой, равной массе всей системы, под действием только внешних сил.
Проектируя (3.8) на оси координат получим дифференциальные уравнения движения центра масс
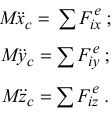
Следствия из теоремы:
1) если 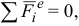 то
то 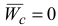 и
и 
2) если 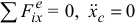 и
и 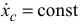 и если
и если 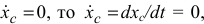 откуда
откуда 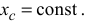
Следствия из теоремы о движении центра масс выражают закон сохранения движения центра масс системы.
Теорема об изменении количества движения механической системы
Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количеств движения всех материальных точек системы
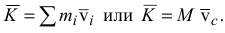
Вектор количества движения тела имеет направление вектора скорости центра масс этого тела.
Дифференцируя уравнения (3.9), получим:
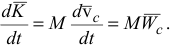
С учетом (3.7) уравнение (3.10) примет вид
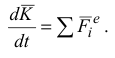
Производная по времени от вектора количества движения системы равна геометрической сумме внешних сил, действующих на эту систему. В проекциях на оси координат уравнение (3.11) запишется
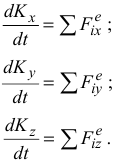
Уравнения (3.12) представляют собой дифференциальную форму теоремы об изменении количества движения системы.
Для получения другой формы рассматриваемой теоремы введем понятие импульса силы.
Если на тело действует постоянная сила 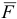 в течение конечного промежутка времени
в течение конечного промежутка времени 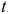 , то импульс силы
, то импульс силы 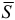 определяется по формуле
определяется по формуле
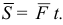
Импульс силы есть вектор, направленный так же, как сила 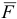 . Для переменной силы сначала определяем элементарный импульс
. Для переменной силы сначала определяем элементарный импульс
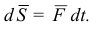
Импульс силы за конечный промежуток времени определяют по формуле
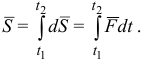
Интегрируя равенство (3.11), получим:
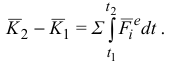
Учитывая (3.13), в окончательном виде полученное уравнение запишется:
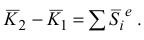
Изменение количества движения системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, приложенных к системе за этот промежуток времени.
Уравнение (3.13) выражает теорему об изменении количества движения системы в интегральной форме.
В проекциях на оси координат уравнение (3.14) имеет вид
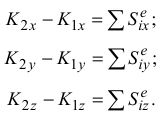
Следствия из теоремы на основании уравнений (3.11) и (3.12):
- Если
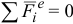 , то
, то 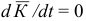 и
и 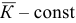 .
. - Если
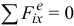 то
то 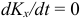 и
и 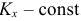 .
.
Эти следствия выражают закон сохранения количества движения систем.
Теорема об изменении кинетического момента механической системы
Момент количества движения материальной точки относительно центра 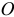 (рис. 3.1).
(рис. 3.1).
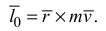
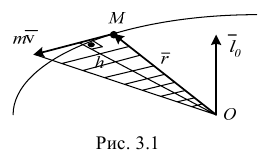
Модуль вектора 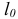 равен
равен
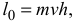
где 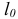 — момент количества движения точки относительно центра
— момент количества движения точки относительно центра 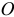 ;
; 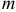 — масса точки;
— масса точки; 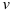 — скорость точки;
— скорость точки; 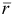 — радиус-вектор, определяющий положение точки
— радиус-вектор, определяющий положение точки 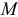 относительно центра
относительно центра 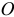 .
.
Момент количества движения точки относительно оси 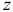
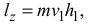
где 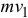 — проекция вектора количества движения на плоскость
— проекция вектора количества движения на плоскость 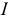 , перпендикулярную оси
, перпендикулярную оси 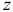 ;
;
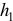 — кратчайшее расстояние от вектора (
— кратчайшее расстояние от вектора (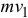 ) до оси
) до оси 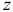 ;
;
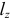 может быть положительным или отрицательным, что определяется по аналогии с моментом силы относительно оси. Зависимость между
может быть положительным или отрицательным, что определяется по аналогии с моментом силы относительно оси. Зависимость между 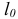 и
и 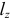 следующая (рис. 3.2):
следующая (рис. 3.2):
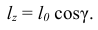
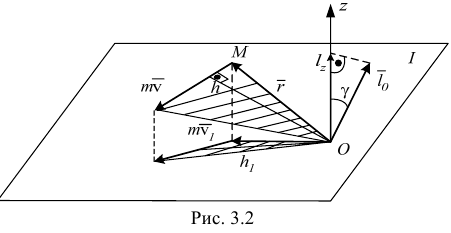
Кинетическим моментом, или главным моментом количеств движения механической системы относительного данного центра, называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого центра
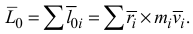
Кинетическим моментом, или главным моментом количеств движения механической системы относительно оси, называется алгебраическая сумма моментов количеств движения всех материальных точек системы относительно оси
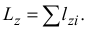
Кинетический момент твердого тела относительно неподвижной оси вращения равен
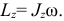
Рассмотрим движение механической системы, состоящей из 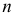 материальных точек. Выделим из системы
материальных точек. Выделим из системы 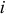 -ю точку и запишем дифференциальное уравнение ее движения
-ю точку и запишем дифференциальное уравнение ее движения
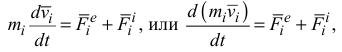
где 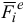 и
и 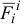 — равнодействующие соответственно внешних и внутренних сил, действующих на
— равнодействующие соответственно внешних и внутренних сил, действующих на 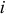 -ю точку.
-ю точку.
Положение 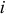 -й точки относительно некоторого центра
-й точки относительно некоторого центра 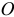 зададим радиусом-вектором
зададим радиусом-вектором 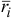 . Левую и правую части уравнений (3.17) векторно умножим на
. Левую и правую части уравнений (3.17) векторно умножим на 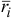

Преобразуем полученное уравнение
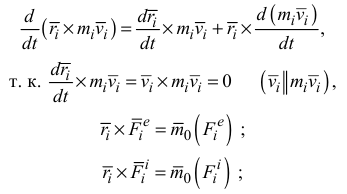
где 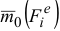 и
и 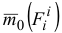 — моменты сил
— моменты сил 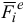 и
и 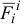 относительно центра
относительно центра 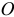 . Уравнение (3.18) запишем в виде
. Уравнение (3.18) запишем в виде
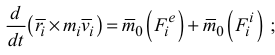
Запишем аналогичные уравнения для всех других точек системы и просуммируем их
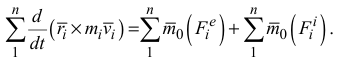
В полученном уравнении
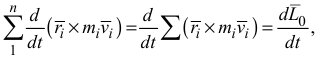
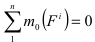
на основании свойства внутренних сил. С учетом отмеченных условий уравнение (3.18) запишется в виде
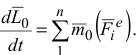
Уравнение (3.17) выражает теорему об изменении кинетического момента механической системы относительно центра.
Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов внешних сил, действующих на эту систему относительно того же центра.
Записывая равенство (3.17) в проекциях на оси координат, получаем:

где 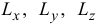 — кинетические моменты механической системы относительно осей координат.
— кинетические моменты механической системы относительно осей координат.
Следствия из теоремы на основании уравнений (3.20) и (3.21):
- Если
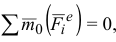 то
то 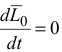 и
и 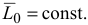
- Если
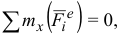 то
то 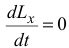 и
и 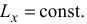
Следствия из теоремы об изменении кинетического момента механической системы выражают закон сохранения кинетического момента механической системы.
Теорема об изменении кинетической энергии механической системы
Кинетическая энергия механической системы определяется как сумма кинетических энергий всех входящих в эту систему материальных точек
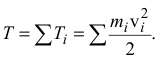
Кинетическая энергия твердого тела
Формулы, определяющие кинетическую энергию тела при различных видах движения.
1) Поступательное движение

где 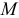 — масса тела;
— масса тела; 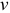 — скорость тела.
— скорость тела.
2) Вращение твердого тела вокруг неподвижной оси
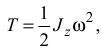
где 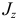 — момент инерции тела относительно оси вращения;
— момент инерции тела относительно оси вращения; 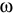 — угловая скорость тела.
— угловая скорость тела.
3) Плоскопараллельное движение
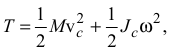
где 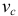 — скорость центра масс тела;
— скорость центра масс тела;
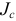 — момент инерции относительно оси, проходящей через центр масс перпендикулярно плоскости движения.
— момент инерции относительно оси, проходящей через центр масс перпендикулярно плоскости движения.
В общем случае движения твердого тела кинетическая энергия определяется по формуле
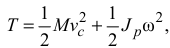
где 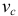 — скорость его центра масс;
— скорость его центра масс; 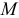 — масса тела;
— масса тела;
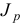 — момент инерции тела относительно мгновенной оси, проходящей через центр масс;
— момент инерции тела относительно мгновенной оси, проходящей через центр масс;
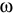 — угловая скорость вращения тела относительно мгновенной оси.
— угловая скорость вращения тела относительно мгновенной оси.
Кинетическая энергия в общем случае движения твердого тела равна сумме кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращательного движения вокруг мгновенной оси, проходящей через центр масс (теорема С. Кен ига).
Вывод теоремы об изменении кинетической энергии механической системы проводят, используя уравнение теоремы для точки, т. к. она справедлива для любой из точек системы. Тогда для каждой точки системы массой 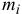 , движущейся со скоростью
, движущейся со скоростью 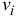 , можно записать:
, можно записать:
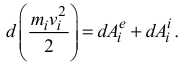
Интегрируя это равенство, получаем:
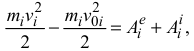
где нижний индекс
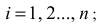
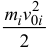 — кинетическая энергия точки в начальном положении системы;
— кинетическая энергия точки в начальном положении системы;
 — кинетическая энергия точки в конечном положении системы;
— кинетическая энергия точки в конечном положении системы;
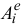 — алгебраическая сумма работ внешних сил, действующих на точку на заданном перемещении;
— алгебраическая сумма работ внешних сил, действующих на точку на заданном перемещении;
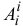 — алгебраическая сумма работ внутренних сил на том же перемещении.
— алгебраическая сумма работ внутренних сил на том же перемещении.
Просуммируем левые и правые части уравнений (3.27)
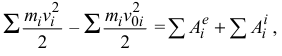
где 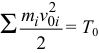 — кинетическая энергия системы в начальном положении;
— кинетическая энергия системы в начальном положении;
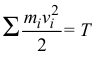 — кинетическая энергия системы в конечном положении.
— кинетическая энергия системы в конечном положении.
Тогда равенство (3.28) будет иметь вид
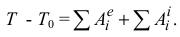
Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.
Если
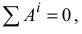
то такая система называется неизменяемой. Тогда уравнение (3.25) примет вид
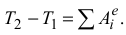
Работа сил
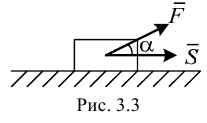
1) Работа постоянной силы
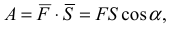
где 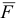 — постоянная сила;
— постоянная сила;
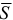 — вектор перемещения точки приложения силы;
— вектор перемещения точки приложения силы; 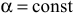 — угол между векторами
— угол между векторами 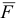 и
и 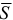 .
.
Работа силы есть алгебраическая величина, равная произведению модуля силы на перемещение точки приложения силы и на косинус угла между векторами 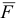 и
и 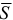 (рис. 3.3).
(рис. 3.3).
2) Если сила переменная, то сначала определяется элементарная работа
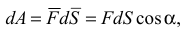
а затем работа силы на конечном перемещении определяется по формуле
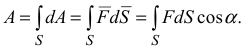
3) Элементарная работа силы через проекции векторов 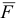 и
и 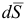 на координатные оси может быть записана в виде
на координатные оси может быть записана в виде
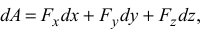
где 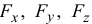 — проекции вектора силы
— проекции вектора силы 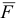 на координатные оси;
на координатные оси;
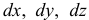 — проекции вектора
— проекции вектора 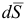 на те же оси.
на те же оси.
При определении работы силы на конечном перемещении с помощью формулы (3.33) получим
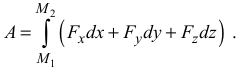
4) Работа силы, приложенной к вращающемуся телу:
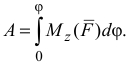
Если 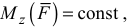 то
то 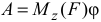 , где
, где 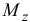 — момент силы относительно оси;
— момент силы относительно оси; 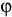 — угол поворота тела. Работа положительная, если направление момента совпадает с направлением углового перемещения тела, и отрицательная в противном случае.
— угол поворота тела. Работа положительная, если направление момента совпадает с направлением углового перемещения тела, и отрицательная в противном случае.
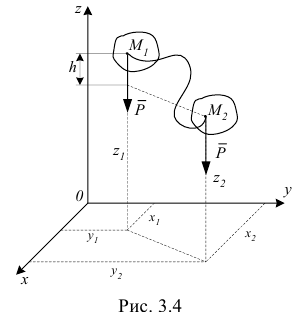
5) Работа силы тяжести (рис. 3.4)
При перемещении точки 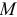 на неё действует сила тяжести
на неё действует сила тяжести 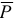 . Вычислим работу этой силы на перемещении
. Вычислим работу этой силы на перемещении 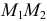 по формуле (3.3)
по формуле (3.3)
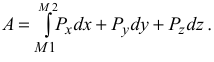
Проекции силы 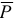 на оси координат будут
на оси координат будут
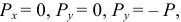
тогда уравнение (3.3) примет вид
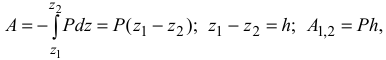
где 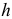 — вертикальное перемещение точки приложения силы.
— вертикальное перемещение точки приложения силы.
Работа силы тяжести не зависит от вида траектории, по которой перемещается точка, а зависит лишь от высоты, на которую опускается или поднимается точка приложения силы тяжести. Работа положительная, если конечное положение точки ниже начального, и работа отрицательная, если конечное положение точки выше начального.
6) Работа силы упругости
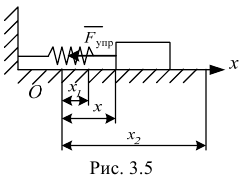
На рис. 3.5 показан в промежуточном положении груз, прикрепленный к пружине. Начало оси 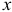 совмещено с положением статического равновесия, поэтому в промежуточном положении пружина растянута на величину
совмещено с положением статического равновесия, поэтому в промежуточном положении пружина растянута на величину 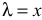 . Тогда
. Тогда 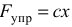 , где
, где 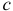 — жесткость пружины,
— жесткость пружины, 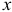 — ее деформация.
— ее деформация.
Проекция 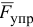 на оси равны:
на оси равны:
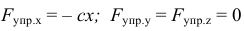
Подставив эти значения в формулу (3.34), получим:
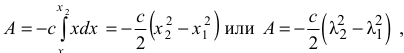
где 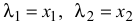 — деформация пружины в начальном и конечном положениях тела (системы).
— деформация пружины в начальном и конечном положениях тела (системы).
Если в начальном положении деформация пружины равна нулю, т. е. 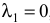 , то формула (3.36) принимает вид
, то формула (3.36) принимает вид
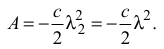
В общем случае работа упругой силы может быть положительной и отрицательной.
Работа положительная, если деформация пружины уменьшается при перемещении тела, и отрицательная, если деформация пружины увеличивается.
7) Для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении
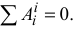
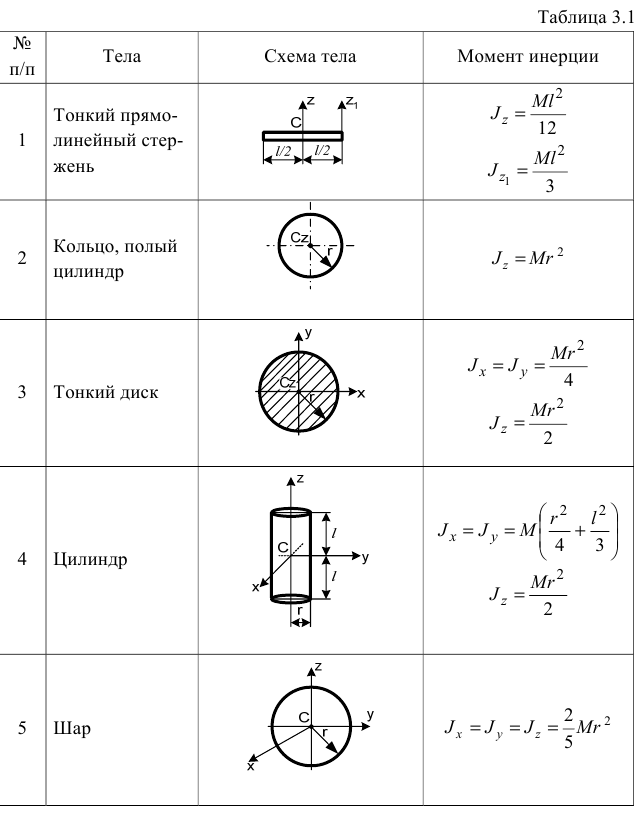
Для решения определенного рода задач надо знать моменты инерции твердого тела. Моменты инерции некоторых однородных твердых тел приведены в табл. 3.1.
Если задан радиус инерции твердого тела, то момент инерции относительно оси, проходящей через центр масс, определяется по формуле 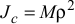 , где
, где 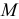 — масса тела,
— масса тела, 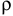 — радиус инерции.
— радиус инерции.
Возможно эта страница вам будет полезна:
| Контрольная работа по теоретической механике |
Готовые курсовые работы:
- Курсовая работа Д2 Каток сплошной однородный цилиндр. Определить — скорость тела 1 (рис. Д2).
- Курсовая работа ДЗ Дано: массы тел соответственно равны Закон движения тела 3 осуществляется по закону ; см. рис. ДЗ. Найти перемещение призмы 1 по идеально гладкой плоскости. В начальный момент система находилась в покое.
Принцип Даламбера
Для рассмотрения движения систем Даламбер предложил специальный принцип, получивший название принципа Даламбера.
Принцип Даламбера для материальной точки эквивалентен основному закону динамики. Уравнение движения материальной точки массой 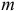 относительно инерциальной системы отсчета под действием приложенных активных сил и реакций связей имеет вид
относительно инерциальной системы отсчета под действием приложенных активных сил и реакций связей имеет вид
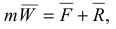
где 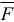 — равнодействующая активных сил;
— равнодействующая активных сил;
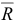 — равнодействующая реакций связей;
— равнодействующая реакций связей;
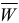 — ускорение точки относительно инерциальной системы отсчета.
— ускорение точки относительно инерциальной системы отсчета.
Представим (3.40) в виде 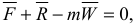 введем обозначение
введем обозначение
 — сила инерции материальной точки, тогда получим
— сила инерции материальной точки, тогда получим
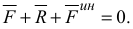
Таким образом, при движении материальной точки активные силы, реакции связей вместе с силой инерции точки образуют уравновешенную систему сил.
Уравнение (3.41) выражает принцип Даламбера для точки.
Рассмотрим систему 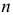 материальных точек. К каждой точке системы приложены равнодействующая активных сил и равнодействующая реакций связей. Применяя принцип Даламбера к каждой точке системы, получим:
материальных точек. К каждой точке системы приложены равнодействующая активных сил и равнодействующая реакций связей. Применяя принцип Даламбера к каждой точке системы, получим:
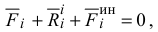
где нижний индекс
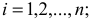
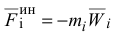
сила инерции 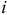 -й точки.
-й точки.
Условие (3.42) можно представить в эквивалентной форме
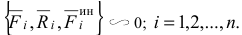
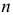 векторных условий (3.42) или (3.43) выражают принцип Даламбера для системы: при движении механической системы активные силы и реакция связей вместе с силами инерции составляют уравновешенную систему сил.
векторных условий (3.42) или (3.43) выражают принцип Даламбера для системы: при движении механической системы активные силы и реакция связей вместе с силами инерции составляют уравновешенную систему сил.
На основании принципа Даламбера для системы в форме (3.43) можно получить шесть уравнений равновесия для сил, действующих на точки системы, включая силы инерции, имеющие пространственное расположение.
Если просуммировать левые части уравнений (3.42) по всем точкам системы, то
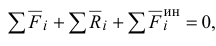
где 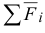 — главный вектор активных сил;
— главный вектор активных сил;
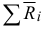 — главный вектор реакций связей;
— главный вектор реакций связей;
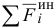 — главный вектор сил инерции.
— главный вектор сил инерции.
Умножая векторно каждое из соотношений (3.42) слева на радиус-вектор точки 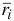 и суммируя по точкам системы, получаем:
и суммируя по точкам системы, получаем:
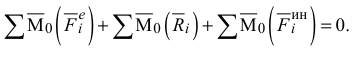
Условия (3.44) и (3.45), если выразить их через проекции на координатные оси, дадут шесть условий равновесия, аналогичных условиям равновесия сил, приложенных к твердому телу, в статике.
Здесь 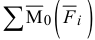 — сумма моментов активных сил относительно точки
— сумма моментов активных сил относительно точки 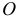 . (главный момент активных сил);
. (главный момент активных сил);
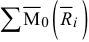 — сумма моментов реакций связей относительно точки
— сумма моментов реакций связей относительно точки 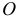 (главный момент реакций связей);
(главный момент реакций связей);
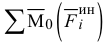 — сумма моментов сил инерции относительно точки
— сумма моментов сил инерции относительно точки 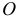 (главный момент сил инерции).
(главный момент сил инерции).
Приведение сил инерции твердого тела
В общем случае движения твердого тела силы инерции точек его образуют произвольную пространственную систему сил инерции, которую в результате приведения к некоторому центру 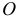 можно заменить одной силой
можно заменить одной силой 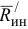 , называемой главным вектором сил инерции, приложенной в центре
, называемой главным вектором сил инерции, приложенной в центре 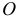 и парой сил с моментом
и парой сил с моментом 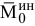 , который является главным моментом сил инерции.
, который является главным моментом сил инерции.
Главный вектор сил инерции не зависит от центра приведения и для любого движения твердого тела равен по модулю произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению

где 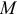 — масса тела,
— масса тела,
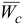 — вектор ускорения центра масс. Для определения главного момента сил инерции рассмотрим несколько частных случаев движения твердого тела.
— вектор ускорения центра масс. Для определения главного момента сил инерции рассмотрим несколько частных случаев движения твердого тела.
1) Поступательное движение
Если твердое тело движется поступательно, то ускорения его точек геометрически равны. Силы инерции этих точек составляют систему параллельных сил, равных по величине, направленных в одну сторону. Такая система сил приводится к равнодействующей 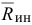 , которая геометрически равна главному вектору сил инерции
, которая геометрически равна главному вектору сил инерции
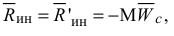
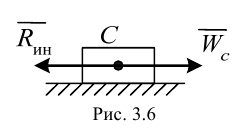
Равнодействующая 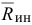 приложена к центру масс и направлена в противоположную сторону вектора ускорения
приложена к центру масс и направлена в противоположную сторону вектора ускорения 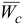 (рис. 3.6).
(рис. 3.6).
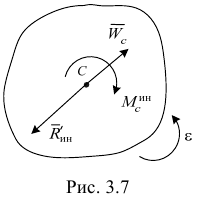
2) Вращение тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной к этой плоскости (рис. 3.7 а).
Если ось вращения не проходит через центр масс, то вследствие симметрии приведенные силы — главный вектор сил инерции и пара сил с моментом, равным главному моменту сил инерции, будут лежать в плоскости симметрии.
Если выбрать за центр приведения точку 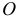 плоскости симметрии, лежащую на оси вращения, то главный вектор сил инерции будет приложен к этой точке и направлен противоположно ускорению центра масс тела (рис. 3.7 б), который определяется по известной формуле
плоскости симметрии, лежащую на оси вращения, то главный вектор сил инерции будет приложен к этой точке и направлен противоположно ускорению центра масс тела (рис. 3.7 б), который определяется по известной формуле
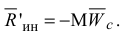
Модуль главного вектора определяется зависимостью
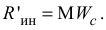
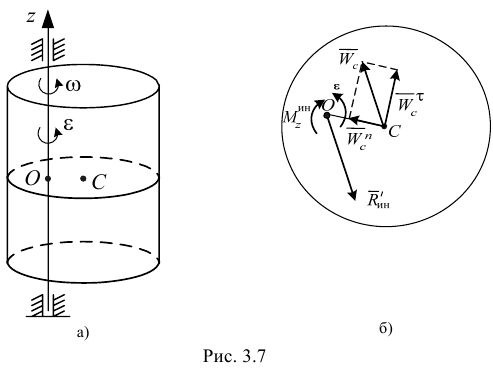
Главный момент сил инерции определим относительно оси 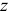
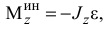
где 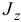 — момент инерции тела относительно оси вращения;
— момент инерции тела относительно оси вращения; 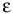 — угловое ускорение тела. Главный момент сил инерции
— угловое ускорение тела. Главный момент сил инерции 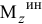 направлен противоположно угловому ускорению.
направлен противоположно угловому ускорению.
Если ось вращения проходит через центр масс, то 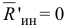 , т. к.
, т. к. 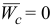
3) Плоскопараллельное движение твердого тела, имеющего плоскость материальной симметрии (рис. 3.8).
Выберем за центр приведения сил инерции центр масс. Тогда вследствие симметрии получим расположенные в плоскости симметрии главный вектор сил инерции, приложенный в центре масс, и пару сил с моментом, равным главному моменту сил инерции. Главный вектор сил инерции найдем по уже известной формуле
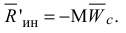
Главный момент сил инерции определим относительно оси, проходящей через центр масс перпендикулярно к плоскости движения тела, по формуле:
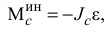
где 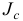 — момент инерции тела относительно названной оси.
— момент инерции тела относительно названной оси.
Главный момент сил инерции направлен в сторону, противоположную угловому ускорению.
Готовая курсовая работа:
Аналитическая механика
В аналитической механике изучается равновесие и движение механических систем.
Классификация связей
Рассмотренные ниже методы решения задач механики применимы не при любых связях, наложенных на систему. Некоторые сведения о связях мы уже имеем (из статики), но их недостаточно.
Рассмотрим вопрос о связях, об их классификации несколько подробнее.
Связями называются любого вида ограничения, которые налагаются на положение и скорости точек механической системы и выполняются независимо от того, какие силы на систему действуют.
Эти ограничения могут быть записаны аналитически с помощью уравнений связей. Например, если известно, что при движении точки выполняется условие
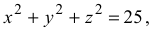
то это означает, что точка движется по сферической поверхности радиусом 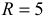 . В общем случае уравнение связи может быть представлено в виде функции
. В общем случае уравнение связи может быть представлено в виде функции
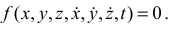
По виду уравнения (3.46) связи классифицируются:
1) на стационарные и нестационарные.
Стационарными связями называются такие связи, уравнения которых не содержат времени в явном виде.
Нестационарные — связи, уравнения которых содержат время в явном виде.
В приведенном выше примере связь стационарная. Для тела, лежащего на полу движущегося лифта, пол является нестационарной связью.
2) На голономные (геометрические) и неголономные (кинематические).
Голономными связями называются такие связи, уравнения которых записаны в виде, не содержащем производных от координат по времени. Такие связи налагают ограничения только на координаты точек системы
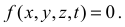
Неголономные — такие связи, которые накладывают ограничение на скорости перемещения точек системы. Уравнения неголономных связей неинтегрируемы и называются неголономными, или неинтегрируемыми.
Пример №1:
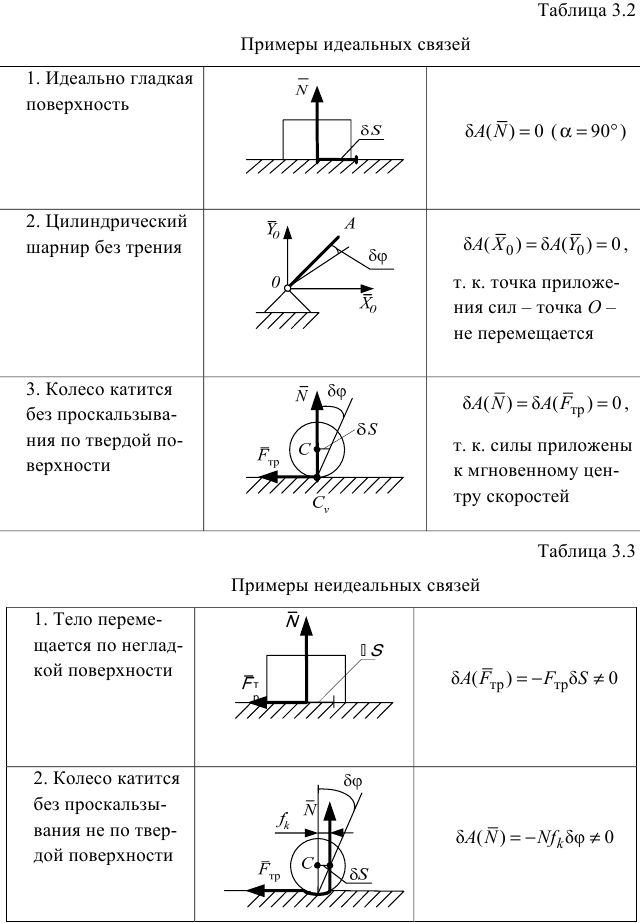
Для колеса, катящегося по поверхности без проскальзывания, выполняется условие, заданное в табл. 3.2 (п. 3).
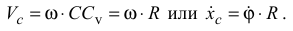
Это уравнение содержит скорости, но его можно проинтегрировать и получить уравнение, содержащее только координаты в виде
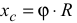
или уравнение
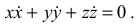
Это уравнение можно записать следующим образом:
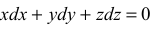
и после интегрирования имеем
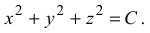
Эти примеры иллюстрируют голономные связи.
Следующий пример уравнения связи
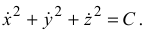
Это уравнение означает, что точка движется с постоянной скоростью, его проинтегрировать нельзя, поэтому рассматриваемая связь него-лономная.
3) На удерживающие (двусторонние) и неудерживающие (односторонние).
Удерживающие — связи, препятствующие перемещению тела (точек) в двух противоположенных направлениях. Уравнения удерживающих связей записываются в виде равенств.
Неудерживающие — связи, препятствующие перемещению тела (точек) в некотором направлении и допускающие перемещение в противоположенном направлении. Уравнения неудерживающих связей записываются в виде неравенств.
Пример №2:
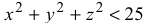
точка может двигаться внутри сферы.
4) На идеальные и неидеальные (табл. 3.2, 3.3).
Идеальными называются связи, если сумма работ реакций связей на любом возможном перемещении системы равна нулю.
Условия идеальности связей записываются так:
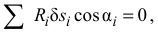
где 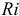 — модуль реакции соответствующей связи;
— модуль реакции соответствующей связи;
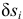 — возможное перемещение;
— возможное перемещение;
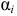 — угол между направлением реакции связи и возможным перемещением точки приложения реакции.
— угол между направлением реакции связи и возможным перемещением точки приложения реакции.
Понятие возможных перемещений будет дано ниже.
Итак, каждой связи можно дать четыре характеристики, относя её к голономной или неголономной, стационарной или нестационарной, удерживающей или неудерживающей, идеальной или неидеальной.
- Возможные перемещения
Понятие возможных перемещений лучше всего проиллюстрировать на примере стационарной голономной связи, которая наложена на одну материальную точку.
Пусть материальная точка лежит на поверхности. Такая связь позволяет точке перемещаться вдоль этой поверхности. Любое из этих бесконечно малых перемещений называется возможным перемещением.
Возможным перемещением системы называется любое бесконечно малое её перемещение, которое допускает связи, наложенные на систему, без их нарушения или разрушения.
Пример №3:
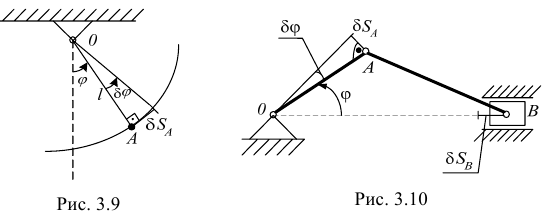
Ввиду малости возможные перемещения точек отсчитываются не по дуге траектории, а по отрезку прямой, направленной по касательной к ней из данного положения, так же как и вектор скорости (перемещение точки 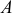
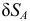 на рис. 3.9, 3.10).
на рис. 3.9, 3.10).
Любой системе можно сообщить бесконечное множество перемещений. Однако для любой из них можно указать некоторое число независимых между собой возможных перемещений, с помощью которых получаются все другие возможные перемещения.
Пример. Для точки, лежащей на плоскости, любое возможное перемещение можно получить через 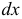 и
и 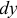 .
.
Число независимых возможных перемещений механической системы с голономными связями равно числу степеней свободы этой системы. На рис. 3.10 показаны разные возможные перемещения 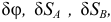 но они взаимозависимы, т. к. система имеет только одну степень свободы.
но они взаимозависимы, т. к. система имеет только одну степень свободы.
- Элементарная работа силы на возможном перемещении
Работа сил на возможном перемещении определяется точно так же, как и работа сил на действительном перемещении. Отличаются они только обозначением. Элементарная работа силы на действительном перемещении обозначается символом 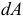 , а элементарная работа силы на возможном перемещении —
, а элементарная работа силы на возможном перемещении — 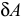 .
.
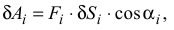
где 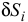 — возможное перемещение точки приложения силы
— возможное перемещение точки приложения силы 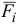 ;
; 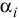 — угол между направлением силы
— угол между направлением силы 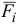 и перемещением
и перемещением 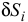 .
.
Принцип возможных перемещений. Пусть механическая система находится в равновесии. Силы, действующие на каждую её точку, уравновешиваются
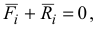
где 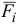 — равнодействующая активных сил;
— равнодействующая активных сил; 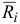 — равнодействующая реакций связей. Дадим системе любое возможное перемещение и вычислим работу всех сил на этом перемещении. Так как силы, приложенные к каждой точке, уравновешиваются, то сумма работ этих сил на перемещении
— равнодействующая реакций связей. Дадим системе любое возможное перемещение и вычислим работу всех сил на этом перемещении. Так как силы, приложенные к каждой точке, уравновешиваются, то сумма работ этих сил на перемещении 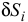 будет равна нулю, учитывая, что
будет равна нулю, учитывая, что 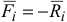 , получим:
, получим:
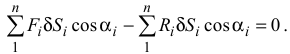
Если связи идеальные, то вторая сумма всегда равна нулю
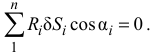
Уравнение работ (3.47) называют общим уравнением статики, оно выражает принцип возможных перемещений.
При равновесии механической системы с идеальными и стационарными связями сумма работ всех активных (задаваемых) сил на любом возможном перемещении системы равна нулю.
- Общее уравнение динамики
По принципу Даламбера механическую систему, движущуюся под действием сил, можно рассматривать как неподвижную, если ко всем точкам системы приложить их силы инерции. Затем можно воспользоваться принципом возможных перемещений.
В уравнение работ (3.46) добавится еще сумма работ сил инерции точек на их возможных перемещениях. При этом получим
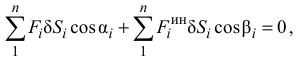
где 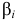 — угол между направлением силы
— угол между направлением силы 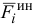 и перемещением
и перемещением 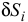 . Уравнение (3.48) называют общим уравнением динамики.
. Уравнение (3.48) называют общим уравнением динамики.
Обозначив
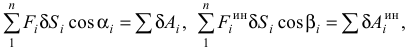
получим уравнение (3.48) в виде:
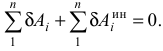
- Обобщенные координаты и обобщенные скорости
Обобщенные координаты — это независимые параметры, заданием которых однозначно определяется положение всех точек механической системы в любой момент времени. У механических систем с голономными (геометрическими) связями число обобщенных координат равно числу степеней свободы. Обобщенные координаты обозначаются буквами
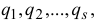
где 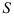 — число степеней свободы системы.
— число степеней свободы системы.
Обобщенные координаты могут иметь любой физический смысл и любую размерность. В механике они могут иметь размерность длины, угла, площади, объема и т. д.
Готовые курсовые работы:
- Курсовая работа Д 8.0 Плоский математический маятник имеет одну степень свободы . В качестве обобщенной координаты можно принять: угол , длину дуги , площадь сектора (рис. 3.11).
- Курсовая работа Д5 Механическая система (рис. Д5) приводится в движение постоянной силой. Каток 2 — сплошной однородный цилиндр. Определить ускорение первого тела .

