Оглавление:
Мы предполагаем, что слово «множество» интуитивно понятно, и не определяем его. Иногда в качестве синонима этому термину используются также слова «пространство», «класс», «семейство», «набор», «совокупность».
Пусть  — некоторое множество. Если
— некоторое множество. Если 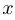 — элемент множества
— элемент множества  , то мы будем записывать этот факт в виде
, то мы будем записывать этот факт в виде 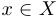 и говорить:
и говорить: 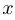 принадлежит множеству
принадлежит множеству  . Значок
. Значок 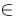 называется знаком принадлежности.
называется знаком принадлежности.
Существует единственное множество, не содержащее ни одного элемента. Это множество называется пустым и обозначается через 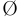 .
.
Общепринятыми являются следующие обозначения:
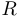 — множество вещественных чисел (отметим, что для нас выражения «вещественной число» и «действительное число» являются синонимами);
— множество вещественных чисел (отметим, что для нас выражения «вещественной число» и «действительное число» являются синонимами); 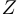 — множество целых чисел;
— множество целых чисел; 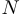 — множество натуральных (то есть целых положительных) чисел;
— множество натуральных (то есть целых положительных) чисел; 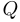 — множество рациональных чисел (то есть таких, которые можно записать в виде
— множество рациональных чисел (то есть таких, которые можно записать в виде 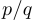 , где
, где 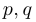 — целые,
— целые, 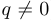 ).
).
Пусть 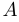 — некоторое подмножество множества
— некоторое подмножество множества  . Это мы будем записывать в виде
. Это мы будем записывать в виде 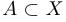 и говорить, что
и говорить, что 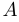 содержится в
содержится в  . Например:
. Например: 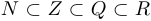 .
.
По договоренности считается, что 0 является подмножеством любого множества и что любое множество является подмножеством самого себя. Подмножество пространства  , которое не совпадает ни с пустым множеством, ни с самим
, которое не совпадает ни с пустым множеством, ни с самим  , называют собственным подмножеством. Если подмножество выделяется каким-либо условием
, называют собственным подмножеством. Если подмножество выделяется каким-либо условием 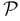 , то это подмножество принято обозначать следующим образом:
, то это подмножество принято обозначать следующим образом: 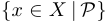 . Например:
. Например: 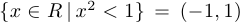 .
.
Набор всех подмножеств множества  обозначается символом
обозначается символом 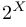 . Происхождение этого символа объясняется тем, что если
. Происхождение этого символа объясняется тем, что если  — конечное множество, состоящее из
— конечное множество, состоящее из 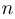 элементов, то число всех подмножеств
элементов, то число всех подмножеств  равно
равно 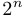 .
.
Объединение и пересечение множеств. Для любых двух множеств 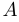 ,
, 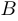 можно определить множества
можно определить множества 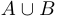 и
и  соответствии с правилами:
соответствии с правилами:

Операции 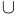 и
и 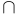 называются операциями взятия объединения (или просто объединением) и взятия пересечения (или просто пересечением). Они удовлетворяют следующим аксиомам:
называются операциями взятия объединения (или просто объединением) и взятия пересечения (или просто пересечением). Они удовлетворяют следующим аксиомам:
коммутативность:

ассоциативность:

взаимная дистрибутивность:
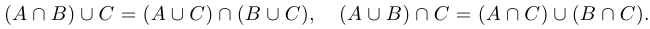
Дополнение к множеству. Для любого подмножества 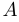 пространства
пространства  мы определяем подмножество
мы определяем подмножество 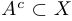 как множество всех точек из
как множество всех точек из  . не принадлежащих
. не принадлежащих 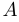 . Формально это записывается так:
. Формально это записывается так: 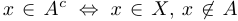 . Это подмножество
. Это подмножество 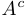 называется дополнением к
называется дополнением к 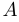 . Операция перехода от множества
. Операция перехода от множества 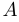 к множеству
к множеству 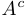 называется операцией взятия дополнения.
называется операцией взятия дополнения.
Значок «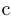 » в качестве верхнего индекса к обозначению множества является первой буквой английского слова «complement» — «дополнение». (Многие авторы взятие дополнения обозначают по-другому:
» в качестве верхнего индекса к обозначению множества является первой буквой английского слова «complement» — «дополнение». (Многие авторы взятие дополнения обозначают по-другому: 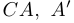 или
или 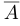 .)
.)
При этом выполняются следующие свойства, которые называются правилами де Моргана:
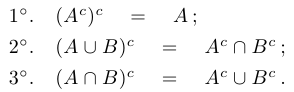
Разность множеств. Разностью  двух множеств
двух множеств 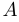 и
и 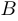 называется множество точек, которые принадлежат
называется множество точек, которые принадлежат 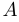 и не принадлежат
и не принадлежат 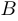 , то есть
, то есть 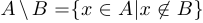 , или, другими словами,
, или, другими словами, 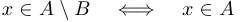 и
и 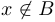 .
.
Отметим, что разность множеств не является коммутативной, ассоциативной или дистрибутивной операцией. Ее свойства можно получить из представления через рассмотренные ранее операции взятия пересечения и дополнения, а именно справедливо следующее тождество:
Представление разности: 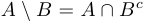 .
.
Симметрическая разность множеств. Симметрической разностью 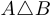 двух множеств
двух множеств 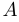 и
и 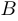 называется множество точек, которые принадлежат
называется множество точек, которые принадлежат 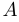 или
или 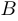 (то есть
(то есть 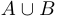 ) и не принадлежат
) и не принадлежат 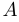 и
и 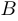 одновременно (то есть не входят в
одновременно (то есть не входят в  ). Таким образом,
). Таким образом, 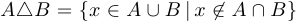 .
.
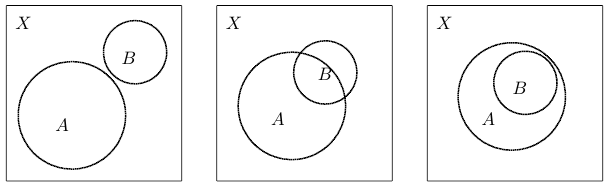
Упр. 1. На всех трех изображенных схемах укажите объединения, пересечения, дополнения и симметрические разности множеств 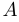 и
и 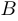 .
.
Пример 1.
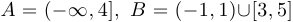 .
.
Решение:
Тогда 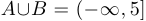 ;
; 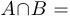
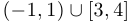 ;
; 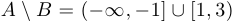 ;
; 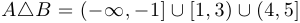 .
.
Пример 2.
Найти 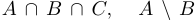 , если
, если 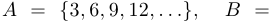
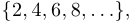
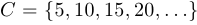 .
.
Решение:
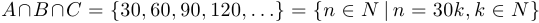 ;
; 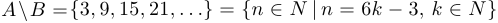 .
.
Три способа доказательства тождеств
1-й способ, или доказательство «по определению». При доказательстве этим способом мы должны показать, что если некоторый элемент 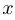 принадлежит множеству, определяемому левой частью равенства, то он принадлежит и множеству, определяемому правой частью, и наоборот.
принадлежит множеству, определяемому левой частью равенства, то он принадлежит и множеству, определяемому правой частью, и наоборот.
Пример 3.
Доказать, что для произвольных множеств 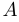 ,
, 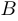 верно, что
верно, что 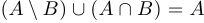 .
.
Решение:
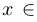 левой части
левой части 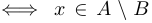 или
или 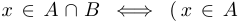 и
и 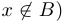 или
или  правой части.
правой части.
2-й способ, или диаграммы Венна. Диаграммами Венна (также диаграммами Эйлера — Венна или кругами Эйлера) называются схемы, на которых произвольные множества 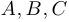 изображены кругами, находящимися в так называемом «общем положении», то есть расположенными так, что все попарные пересечения и общее пересечение всех трех множеств непустые, причем ни одно из множеств не содержит другого, то есть так, как указано на диаграммах внизу. (Если речь идет только о двух множествах, то общим положением считается то, которое указано на центральной из трех схем, изображенных выше.) Тотальное множество
изображены кругами, находящимися в так называемом «общем положении», то есть расположенными так, что все попарные пересечения и общее пересечение всех трех множеств непустые, причем ни одно из множеств не содержит другого, то есть так, как указано на диаграммах внизу. (Если речь идет только о двух множествах, то общим положением считается то, которое указано на центральной из трех схем, изображенных выше.) Тотальное множество  при этом обычно изображается квадратом, содержащим все три круга.
при этом обычно изображается квадратом, содержащим все три круга.
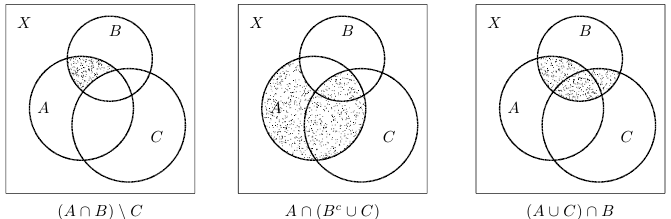
Для того чтобы выяснить, является ли тождеством теоретико-множественное равенство, левая и правая части которого задаются цепочками указанных выше операций с тремя произвольными множествами, следует изобразить отдельно левую и отдельно правую части. Равенство является тождеством тогда и только тогда, когда эти изображения совпадут. Отметим, что если в равенстве участвуют более трех различных множеств, то сказанное неверно: совпадение изображений не является достаточным условием тождественного равенства (для четырех и более множеств на плоскости сложнее понять, что означает термин «общее положение»).
Пример 4.
Верно ли равенство 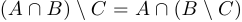 ?
?
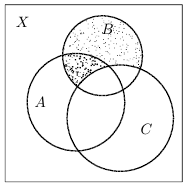
Решение:
Левая часть равенства представлена выше на левой диаграмме. Правая часть представлена справа, причем на диаграмме множество  выделено мелкой пылью, а вся правая часть — более жирно. Указанные множества совпадают; следовательно, равенство является тождеством.
выделено мелкой пылью, а вся правая часть — более жирно. Указанные множества совпадают; следовательно, равенство является тождеством.
Условные тождества доказываются теми же способами, например с помощью диаграмм Венна, однако круги при этом изображаются так, чтобы они удовлетворяли указанным условиям. Очень часто доказательство простейших условных тождеств происходит непосредственно, по определению.
Упр. 2. Проиллюстрируйте на простейшей диаграмме выполнение двух следующих условных тождеств:
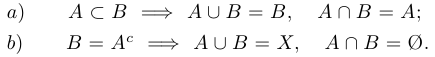
Пример 5.
Доказать, что 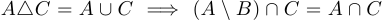 .
.
Решение:
Условие 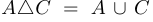 означает, что
означает, что 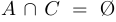 , то есть множества
, то есть множества 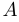 и
и 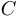 не пересекаются, а раз так, то и
не пересекаются, а раз так, то и 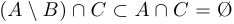 .
.
3-й способ, или доказательство, использующее свойства операций. Этот способ требует некоторой тренированности и более употребителен в случаях, когда надо упростить громоздкие теоретико-множественные конструкции.
Пример 6.
Доказать равенства:
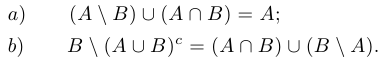
Решение:
a) левая часть 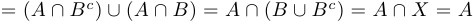 ;
;
b) левая часть 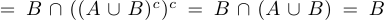 , правая часть
, правая часть 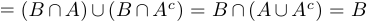 . Таким образом, левая часть равна правой части. Тождество доказано.
. Таким образом, левая часть равна правой части. Тождество доказано.
Пример 7.
Доказать равенства:
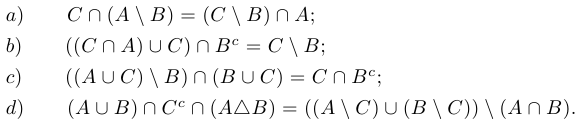
Решение:
a) левая часть 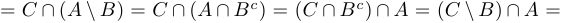 правая часть;
правая часть;
b) 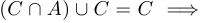 левая часть
левая часть 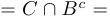 правая часть;
правая часть;
c) левая часть 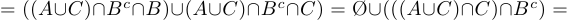
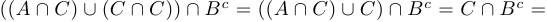 правая часть;
правая часть;
d) несложно проверить, что 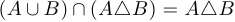 , откуда следует, что левая часть равна
, откуда следует, что левая часть равна 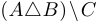 . Однако и
. Однако и 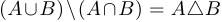 . Следовательно, правая часть равна левой.
. Следовательно, правая часть равна левой.
Декартовым, или прямым, произведением 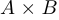 двух множеств
двух множеств 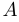 и
и 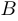 называется множество пар
называется множество пар 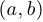 таких, что
таких, что 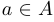 и
и 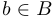 .
.
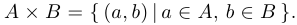
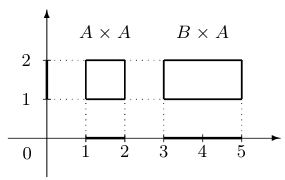
Пример 8.
 . Прямым произведением
. Прямым произведением  является квадрат, а
является квадрат, а  — прямоугольник.
— прямоугольник.
Решение:
Отметим, что множество 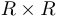 обозначается через
обозначается через 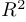 ;
; 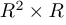 — через
— через 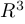 и так далее. Таким образом, множество
и так далее. Таким образом, множество 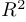 мы идентифицируем с плоскостью, в которой задана декартова система координат, и, следовательно, каждая точка плоскости определяется парой вещественных чисел, называемых координатами этой точки.
мы идентифицируем с плоскостью, в которой задана декартова система координат, и, следовательно, каждая точка плоскости определяется парой вещественных чисел, называемых координатами этой точки.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: функции |
| Курсовая работа на тему: логические функции |
| Курсовая работа на тему: выпуклые множества и функции |
| Курсовая работа на тему: оптимизационные задачи |

