Оглавление:



Кручение упругих стержней сплошного профиля
- Кручение стержня непрерывного профиля эластичное. Реализация теоремы о тангенциальном кольце циркуляции напряжений является критерием, позволяющим отличить его от состояния бесчисленных статически возможных напряжений, реализуемых в реальности скручиванием упругого стержня.
Например, легко видеть, что Формулы тангенциального напряжения и угла кручения круговых стержней удовлетворяют требованиям теоремы циркуляции, поэтому решение кругового сечения
является точным. Теория упругости устанавливает дифференциальное Людмила Фирмаль
уравнение в частных производных, удовлетворяющее напряжению кручения стержня произвольного сечения. Существует метод решения этих уравнений, который позволяет изучать кручение поперечного сечения стержня овальной, веерообразной, прямоугольной и многих других форм.
Величина, которая нас интересует на практике, — это угол скручивания в зависимости от крутящего момента и наибольшего тангенциального давления. Для всех случаев результаты исследования методом теории упругости, которые мы считаем элементарными, могут быть представлены в следующем виде:
- Здесь C — так называемая геометрическая жесткость; Царь ТГК-момент сопротивления кручению. Для круглого диаметра D стержня (92.1) Наружный диаметр d и внутренний диаметр для полого цилиндра DJ (92.2) Для тонкостенных стержней закрытого профиля (92.3) 200 кручение[Глава VII ф Для тонкостенных стержней открытого профиля C=4 2 6 ′ H>=(92.4) ° ^ umax проблема скручивания прямоугольных стержней имеет большое практическое значение.
Рассмотрение этой задачи элементарными средствами невозможно, а метод теории упругости позволяет получить представления углов напряжения и кручения в виде бесконечных рядов. Как оказалось, наибольшее натяжение t получается в середине длинной стороны (L и A’FIG. 130). Хотя в углах напряжения есть второе максимальное напряжение, которое равно нулю, в середине короткой стороны(B и D’)、- т. Напряжение t ’в этих точках меньше, чем напряжение t в точках A и A’. Но если представить себе прямоугольную, цилиндрическую емкость,
в которой циркулирует жидкость, то такая качественная картина откроется. Людмила Фирмаль
Очевидно, что в поворотах скорость будет равна нулю. То же самое количество жидкости, что и секция Oa, протекает через секцию OA в единицу времени, и средняя скорость сегмента OA больше, чем сегмент OA, что, конечно же, является правдоподобным рассуждением, основанным на интуиции, а не доказательстве. Точное представление о характере распределения напряжений можно получить только с помощью теории упругости или точного решения задачи по экспериментальным данным. Что касается распределения напряжения, то последнее всегда является косвенным, так как нет способа измерить напряжение напрямую.
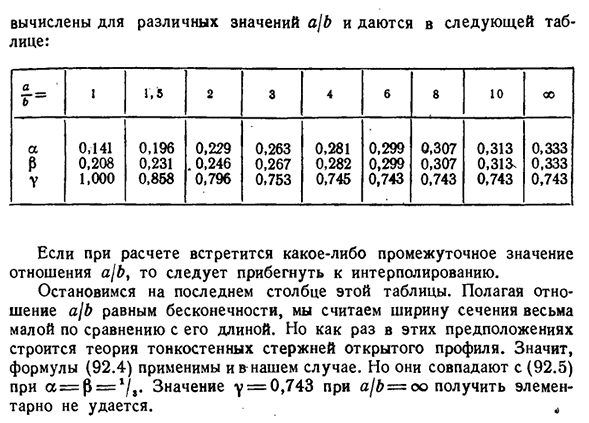
Результаты точного решения показаны следующим образом: 130. С=АА*,WК=$\АБ(92.5) Где A-длинная сторона, А B-короткая сторона прямоугольника. Наконец, напряжение в середине короткой стороны x ’ связано с максимальным отношением напряжения x х’ = ут. Безразмерные коэффициенты a, 0 и y зависят только от одного безразмерного параметра, т. е. отношения ajb, характеризующего сечение. Формула для коэффициентов в функции параметра a/B не может быть записана в конечной форме. Эти коэффициенты§ 93] экспериментальное исследование кручения 201 Рассчитано для различных значений ajb и показано в следующей таблице:
a_b~1G, 5 2 3 4b8 10OO Да, 0.,141 0,196 0,229 0,263 0,281 0,299 0,307 0,313 0,333 ₽ 0,208 0,231. 0.246 0.267 0.28299 0.307 0.313, 0.333 У1, 000 0.858 0.796 0.753 0.745 0.743 0.743 0.743 Если вы найдете промежуточное значение AJB в вычислении, вы должны использовать интерполяцию. Давайте сосредоточимся на последнем столбце этой таблицы. Предполагая, что отношение ajb равно бесконечности, мы предполагаем, что ширина секции очень мала по сравнению с ее длиной. Однако в этих постулатах строится теория тонкостенных стержней открытого профиля. Поэтому в данном случае применима формула (92.4). Но они соответствуют a=P=(92.5) 1/,. При значении y=0,743 ajb-OO, вы не можете получить базу.
Смотрите также:

