Оглавление:



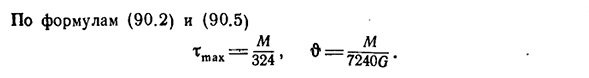

Кручение тонкостенных стержней замкнутого профиля
- Кручение тонкостенного стержня с замкнутым профилем. Рассмотрим тонкостенный стержень, поперечное сечение которого окружено двумя замкнутыми кривыми. Толщина стенки d является функцией дуги средней линии y, которая отсчитывается от любой точки. Если толщина стенки невелика, то нет оснований рассматривать тангенциальное напряжение, которое изменяется по толщине.
Мы считаем, что они зависят только от координат S. Распределение касательных напряжений между кручениями таких тонкостенных стержней визуально аналогично течению жидкости между двумя жесткими стенками, а вектор скорости соответствует вектору напряжений. При условии, что контуры вектора
контактных напряжений направлены к контурам соответствующих Рис 124 Людмила Фирмаль
Условия обтекания жестких непроницаемых стенок. Установленная аналогия все еще чисто внешняя и качественная. Это будет точно основано на следующей теореме: произведение касательного напряжения на толщину стенки является постоянной величиной. Рассмотрим равновесие элемента mnqp, вырезанного из стержня, как показано на рисунке. 124
по закону пары касательных напряжений в продольном сечении, на плоскости тр, находится (фиг. 124), существует касательное напряжение t, равное напряжению поперечного сечения. Сила, действующая на лицо TRR’t’is x&dz. Фронт Nqq ’ ri отделен от первого расстояния ds по дуге средней линии контура. Сила, действующая на эту поверхность, равна x&d z — {- ^(T ftd z) d s.: Ш=о.
- И так оно и есть. Ты то = const. (90.1) Когда тангенциальное напряжение определяется со скоростью текучей среды, условие (90.1) определяется через 90]скручивание тонкого стержня замкнутого профиля 193 Это сейчас Сила, действующая Каждая секция одновременно пропускает один и тот же объем жидкости. В противном случае это несжимаемое состояние жидкости. Здесь можно связать величину тангенциального напряжения при кручении тонкого замкнутого стержня с крутящим моментом.
Нарисуйте поперечное сечение в виде контура, основанного на толщине(рис. 125), видно, что тангенциальная сила TB, величина которой постоянна, действует на единицу длины. Дуги элемента DS зависит от мощности RFID на С; это необязательно, т. о., чтобы при создании ДМ. В этой точке имеется вертикальная точка p, которая опускается от точки по касательной к контуру. Но произведение pds удваивает площадь треугольника с вершинами основания ds и O; назовем его 2dF. Затем D м=(Р6) 2Д Ф.
Если добавить все бесконечные моменты ко всем элементам контура, то получится: М=х b2f по. Людмила Фирмаль
Где K-площадь, ограниченная профилем поперечного сечения. И так оно и есть. _М Х ~ 2Ф д’(90.2) Последний нерешенный вопрос-это решение угла скручивания. Для этого мы докажем теорему, называемую теоремой о тангенциальном кольце циркуляции напряжений. В связи с гипотезой жестких контуров, как уже говорилось, деформация стержня рассматривается как вариант, связанный с вращением всего сечения и смещением элементов Мнкр, возникающим при перемещении точки поперечного сечения вдоль шины (рисунок). 124), рассмотрим его как результат двух последовательных сдвигов: г=г’+г»-
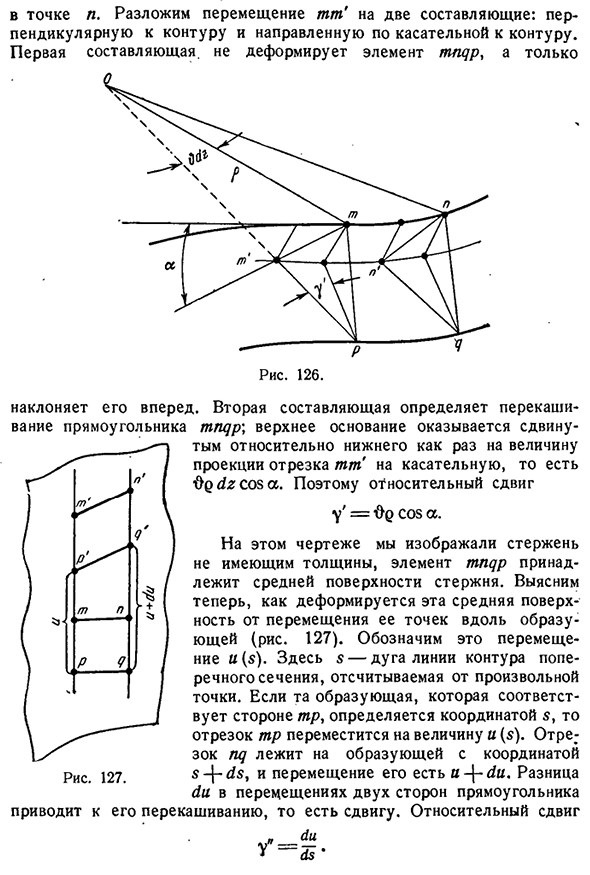
Во-первых, давайте определим значение y’ — сдвиг при вращении секции. Соответствующая структура состоит из фигур. Два бесконечно близких участка, взятых на расстоянии dz, то есть 126, вращаются один относительно другого на угол$d z. точка T, в результате вращения, получает смещение TT’(равное Oq dz) вдоль дуги окружности с центром точки O. 7ю. N. Rafotov194 кручение[Глава VII В точке p движение ’ TT ’ раскладывается на две составляющие: перпендикулярную контуру и касательную к контуру. Первый компонент не деформирует элемент mnqp、 Он наклоняет ее вперед. Вторая составляющая определяет наклон mnqp
прямоугольника\верхнее основание смещено относительно значения проекции отрезка TT ’ к касательной, это Op dz cos a. Г’=О. потому что. На этом рисунке мы изображаем стержень без толщины, а элемент mnqp принадлежит промежуточной поверхности стержня. Теперь давайте посмотрим, как эта средняя плоскость деформируется, перемещая свои точки вдоль шины (рис. 127). Мы называем это смещением и(b). Здесь s-дуга контурной линии поперечного сечения, отсчитываемая от любой точки. Если произведение, соответствующее стороне Tr, определяется координатой s, то сегмент
Tr перемещается на значение и (s). Сегмент nq находится на изделии с координатой s- / — ds, а его смещение-/ — du. Разница в движении сторон прямоугольника приводит к его искажению, то есть к смещению. Относительный сдвиг » du U§ 9 0] кручение тонкостенных стержней замкнутых профилей 1 9 5 Таким образом, общее значение сдвига И Y=e Q c o s » 4 -^, T=G^o c o s a (90.3)тангенциальное напряжение умножается на ds и интегрируется по контуру. Справа интеграл от, равный разности между значениями начальной и конечной точек интегрального пути, исчезает для замкнутого пути, и мы получаем: (f) x ds=f q cos a ds. Левая часть называется тангенциальной циркуляцией напряжений, а правая часть легко вычисляется. Действительно, обратимся к фигуре. 125, o cos a=p, поэтому отображается Q cos ds==2dF.
И так оно и есть. (фи г Кос ДС = 2Ф, Для угла кручения получено следующее уравнение: (90.4) Тогда значение x определяется по формуле (90.2). Поэтому L м ШПР^~~4Г ф ф ф т’ Я (90.5)) П р и М Е Р1. Т О Н К О с т е н а т р у б р а д и у С А Р, а затем Л О С и Н с. ее F = l/?* , По выражениям (9Q2) и (90.5) находим: т. M_M 2л/? 6 ′ 2л/?тот же результат получается, если трубка » D0 «рассматривается как» круглый полый стержень » и применяется формула§ 87. П р и М Е Р2. Это позволяет повысить производительность вашего приложения. Средняя линия разреза, обозначенная пунктирной линией 128, представляет собой прямоугольник с размерами 9×18×18, а следовательно, F=162 см*. 7 * 196 кручение[гл. VII В соответствии с уравнениями (90.2)и (90.5))
Смотрите также:
| Упруго-пластическое кручение стержня круглого сечения | Кручение тонкостенных стержней открытого профили |
| Гипотеза жесткого контура | Кручение упругих стержней сплошного профиля |

