Оглавление:




Кручение тонкостенных стержней открытого профили
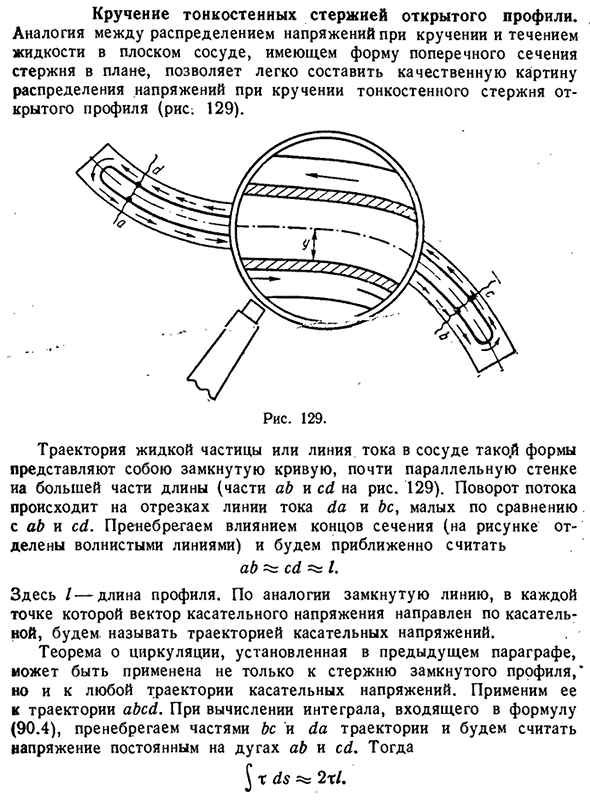
- Скручивание тонкостенных прутков и профилей. Благодаря сходству распределения крутильных напряжений с потоком жидкости в плоском сосуде с формой поперечного сечения стержня можно определить качественное распределение распределения напряжений при кручении тонкостенного стержня открытой формы.
Локус жидких частиц или линий тока в контейнере тако. форма y представляет собой замкнутую кривую, почти параллельную стенкам ia примерно по длине (ab часть и cd часть рисунка). 129). Вращение потока происходит в сегментах текущей линии da и BS и мало по сравнению с ними. с AB и CD. Мы игнорируем влияние краев разреза (рисунок разделен волнистой линией)
и рассматриваем примерно около ab cd I. Вот я-длина профиля. Людмила Фирмаль
Аналогично, замкнутая линия в каждой точке, где вектор касательных напряжений направлен тангенциально, называется траекторией касательных напряжений. Теорема циркуляции, установленная в предыдущем пункте, может быть применена не только к стержням замкнутого профиля, но и к любой траектории касательного напряжения. Примените его к орбите Эбеда.
При вычислении интеграла, входящего в Формулу (90.4), игнорируют части BC и da траектории и учитывают константы напряжения дуги ab и CD. Тогда J t ds=2T/.§ 91] кручение стержня 197 в тонкостенном открытом профиле Таким образом, область F, ограниченная текущей линией с той же точностью, определяется выражением (90.4) 2×1x4G лы-2Г г’ И так оно и есть. Т=2G0y.(91.1)
- Где y-расстояние, на котором тангенциальное напряжение находится от центральной линии профиля. Остается соединить прямой угол, который будет крутить крутящий момент M и Y. часть, заключенную между ними, можно рассматривать как бесконечно тонкий стержень замкнутого профиля, который принимает бесконечно малую часть крутящего момента dM. Примените к нему формулу (90.5): Но как мы уже видели, И так оно и есть. Ф^2л г, д г — ^г г’dd=8Gly*&ды. Чтобы вычислить полный момент, нам нужно объединить это выражение от y=0 до y= -^ -. Возьми: M=±o/b’y. (91.2)
Если вы определяете значение Th из(91.2) и присваиваете его выражению (91.1、: Максимальное значение напряжения достигает там, где y=Y. И так оно и есть. (91.3) Формулы (91.2) и(91.3) указывают на то, что профиль очень тонкий, А d-профиль I. 198 кручение[выведено в предположении, что по сравнению с длиной чап очень мало. VII Таким образом, эта длина зависит только от толщины b, но не от размера I. Кроме того, профиль предполагается гладким, а его радиус кривизны должен
быть большим по сравнению с размером B. В местах сопряжения элементов происходит локальное перераспределение напряжений. Людмила Фирмаль
Его свойства можно понять, обратившись к аналогии гидродинамики. При обтекании поворотов или при резких изменениях поперечного сечения распределение скорости всегда неравномерно. Однако возмущенная зона, или область локального напряжения, простирается относительно длины порядка b от границы раздела элементов профиля. Поэтому, если толщина стенки достаточно мала по сравнению с длиной элементов, составляющих профиль, то игнорируют эти локальные напряжения, и каждый элемент скручивают отдельно, согласно формуле для номера элемента (91.2). / По длине и толщине b, — Come^I Общий или Крутящий момент равен сумме таких частичных моментов,
И так оно и есть. (91.4) M k теперь может определить, некоторые из моментов, которые попадают в число элементов k -. / АБ? Максимальное напряжение числа элементов k, обусловленное формулой (91.3), равно (Т1-М Т>К Ш м я » Д В-Г З а — Наибольшее расчетное давление получается на стержень, имеющий наибольшую толщину: t—M6ma]I (91.5)§ 92] упругое кручение стержня непрерывного профиля 199 На самом деле отношения S/Z всегда конечны, поэтому формулы (91.4) и (91.5) не являются точными. Небольшие корректировки, необходимые для этих формул при расчете фактического профиля, описаны в библиографии.
Смотрите также:
| Гипотеза жесткого контура | Кручение упругих стержней сплошного профиля |
| Кручение тонкостенных стержней замкнутого профиля | Опытное исследование кручения |

