Оглавление:





Кручение тонкостенных стержней
- Кручение тонкостенного стержня Если рассматривать кручение тонкостенных стержней, то метод их расчета может зависеть от того, имеет ли открытый профиль или закрытый профиль поперечное сечение. Если рассматривать кручение замкнутого тонкого профиля (рис. 217), рассмотрим толщину стенки небольшого стержня так, чтобы можно было предположить, что касательное напряжение на нем такое же, как и напряжение в середине толщины стенки.
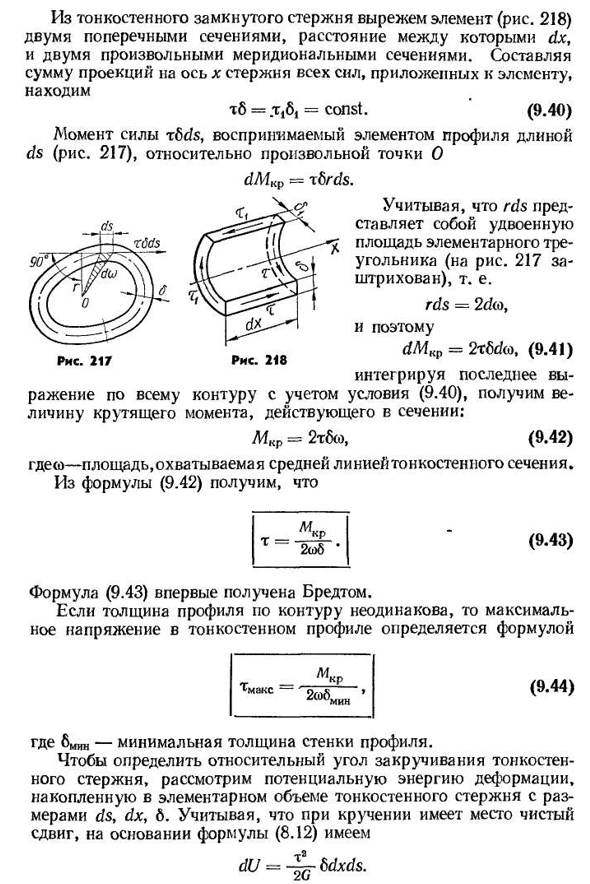
8 8-2770 22. Из закрытой палочки с тонкой стенкой вырежьте элементы (рис. 218) два поперечных сечения, расстояние между которыми равно dx, и два произвольных меридианных сечения. Составьте сумму проекций на оси Х стержней всех сил, приложенных к элементам и、 ТБ=т д = const. (9.40) силовой момент rfids воспринимается профильным элементом длины ds(фиг. 217). Учитывая, что rds в два раза больше площади основного треугольника(на рис. Если мы интегрируем последнее
уменьшение по всему контуру с учетом условия (217 заштриховано), Людмила Фирмаль
т. е. rds=2d&, следовательно, Gicr=2tmo, (9.41) (9.40). Из Формулы (9.42) получаем Формула (9.43) была впервые получена Бредтом. Если толщина контура по контуру не одинакова, то максимальное напряжение тонкостенного сечения определяется по формуле Тмакс ** CR2<об / мин’ Где Bmin-минимальная толщина стенки профиля. Для определения относительного угла кручения тонкостенного стержня рассмотрим потенциальную энергию деформации, запасенную в основном объеме тонкостенного стержня в размерах ds, dx, 6. Учитывая, что твист имеет чистый сдвиг, основанный на Формуле (8.12), мы имеем dU=bdxds. 226 / t2d2 x ds26 6 • Полная энергия
деформации однородного стержня длины I получается интегрированием последнего уравнения по замкнутому контуру вдоль длины I: Ю-Дж. Ф. в^dsdx — подставляя формулу o TB из Формулы (9.42) в правую часть последней Формулы, — M*pl (6) 2G (2w) 2Y B ’ заставит ту же энергию скручиваться через работу внешнего крутящего момента MK-MKR. ICF _ ~2′ Ф4- «=l=2, если мы приравняем правильную часть последней Формулы、 4GV Относительный угол закручивания °=1& — е-т—<«•»> Это выражение может быть выражено в приведенной выше нотации для кручения: 0= = — м»- 6VK’ Куда? 4to2 ’»ДС=<ч Постоянная длина контура при толщине S ми= 4Gc>26 • (9.46) Например, рассматривая скручиван
- ие тонкостенных труб(рис. 219), 6=будет const По формулам (9.43) и (9.46) находим m K? Открытый профиль 2nR * 6′ — 2nR3bG’. Определение крутильных напряжений и деформаций в тонкостенных стержнях открытого профиля Т== В* 127швеллер, двутавровая балка (рис. 220) или угол, можно использовать теорию расчета для торсионных стержней прямоугольного сечения. При этом открытый профиль делится на прямоугольные элементы, толщина которых значительно меньше его длины. Как вы можете видеть из таблицы. 14, такие>10) коэффициенты a и p равны составному профилю на ОС- Прямоугольные элементы(когда 1-’ Основа формулы(9.33)и(9.37)) 4=£л4 б ’ привет — (9-47) Угловой двутавровый Т-образный канал Здесь вводится коэффициент 1], учитывающий
систематизацию фактического профиля. » » Р = 1,00; 1,20; Р=1,15; 1,12 В открытых профилях с тонкими стенками длина элементов обычно обозначается буквой s, а толщина стенок-цифрой 6. Затем, если вы замените выражение (9.47 h) на s и b на 6, вы получите 9-48 Угол кручения определяется по формуле (9.30), максимальное касательное напряжение, возникающее в области с толщиной наибольшей стенки Bmax-по формуле (9.28). Для длинных прямоугольников h в VT ^ЦР^Кех Тмакс-г• * к Затем Рассмотрим пример расчета тонкостенного бруса с открытым профилем. Пример 33. Определите максимальное натяжение и угол кручения стержня длиной 900 мм(рис. 221)
угол 50×50×5 с поперечным сечением в виде равнобедренного треугольника, подверженного крутящему моменту L1K= » = 500kgf * см. модуль сдвига материала стержня G 23 8 * 10^ (9.49) 228 Людмила Фирмаль
максимальное тангенциальное напряжение возникает в середине полки(концентрация входящих угловых напряжений не учитывается). Эти напряжения определяются по формуле (9.49): ^КЛ^Макс Т Макс 1 ″ J K Куда? 1л=ь=^1 =Н-Г-С= 1 • −3-1(5 • 0,53) + ( 4, 5.0.5-3)] CM1=0>4 £ = = 1 ТМ от А до С «- кгс / см»=6 2 5 кгс / см». J r<и, 4 Угол закрутки стержня определяется по формуле (9.30): s9! ^ ^ — 0 — ’»2 5″ Пример 34. Определите натяжение и прямые углы закрутки стальной трубы, разрезанной вдоль шинопровода(рис. 222). Диаметр dn=90mm, внутренний AQ=85mm момент закрутки трубы L4k=500kgf * см. модуль сдвига G=8X106kgf / cm2 материала. Сравните результирующее напряжение и угол скручивания с напряжением
и углом скручивания сплошной трубы. Тангенциальное давление разрезанной трубы определяется по формуле (9.49)): < Т>90 Рис двести двадцать два Куда? Где s-удлиненная длина средней линии участка трубы. Затем Я Один. 4= «u=u» •8.75 * 0.25 ’cm4=0.143 CM4; Tr= — S — =кгс / см2=875 кгс / см». Напряжение сплошной трубы определяется по формуле (9.43): tsp= = — 2F^T o^5 кгс / см=16163 кгс / см — линейный угол скручивания отрезанной трубы M500 b7g=8—Ио■0.143 Р А Д/С М=0>00437Raya/СМ1 Угол закрутки неразрезанной трубы линейный выведен от Формулы (9.46): MKps500l * 8.75 Два. ©Р= Е С П-4Г(0 25 4-8. 10″(ф — * 8.75 ″ Дж.0.25 Радиан/см=0.00000475 Радиан/см. » Таким образом, в сплошной трубе с кручением напряжение меньше в 52,5 раза, а угол кручения в 920 раз больше, чем у трубы, разрезанной вдоль шинопровода.
Смотрите также:
| Расчет валов на прочность и жесткость при кручении | Расчет винтовых цилиндрических пружин |
| Кручение стержней некруглого сечения | Концентрация напряжений при кручении |

