Кривые поверхности

Кривые поверхности

Общие сведения: определения, классификация, термины

В начертательной геометрии поверхность определяется как след движущейся в пространстве линии, называемой образующей. Такое представление об образовании поверхности удобно для графических построений.

Представление об образовании поверхности непрерывным движением линии позволяет такие поверхности называть кинематическими. При этом линия, образующая поверхность, может во время движения деформироваться. Тогда говорят о поверхности с «переменной образующей».

Образующая линия может быть прямой или кривой.

Закон движения образующей может быть задан другими линиями, называемыми направляющими поверхности. По ним образующая в процессе своего движения скользит.

Поверхность, которая образована движением прямой линии, называют линейчатой поверхностью. Таким образом, линейчатая поверхность представляет собой геометрическое место прямых линий.

Поверхность, которая образована движением кривой линии, называют нелинейчатой поверхностью. Примерами такой поверхности является сфера, тор и др.

Одна и та же поверхность может быть образована перемещением различных линий и согласно различным условиям движения, то есть законы образования поверхности в ряде случаев могут быть разнообразными. Для решения геометрических задач, как правило, используют наиболее простой или удобный закон задания поверхности.

Некоторые кривые поверхности могут быть развернуты так, что совместятся все своим точками с плоскостью без разрывов, складок, или растяжений. Такие поверхности называют развертываемыми. К ним относятся только линейчатые поверхности, причем такие, у которых смежные прямолинейные образующие параллельны, или пересекаются между собой, или являются касательными к некоторой пространственной кривой.

Все кривые нелинейчатые поверхности и те линейчатые, которые не могут быть развернуты в плоскость, называются неразвертывающимися (или косыми).

Задать поверхность на чертеже — значит указать условия, позволяющие построить каждую точку этой поверхности. Для задания поверхности достаточно иметь проекции направляющих линий (одной или нескольких) и указать, как строится образующая линия. Для придания же изображениям поверхности наглядности вычерчивают еще и ее очерк, показывают несколько промежуточных положений образующих поверхности, отображая, таким образом, поверхность в виде каркаса.

Обзор некоторых кривых поверхностей, их изображение на чертеже

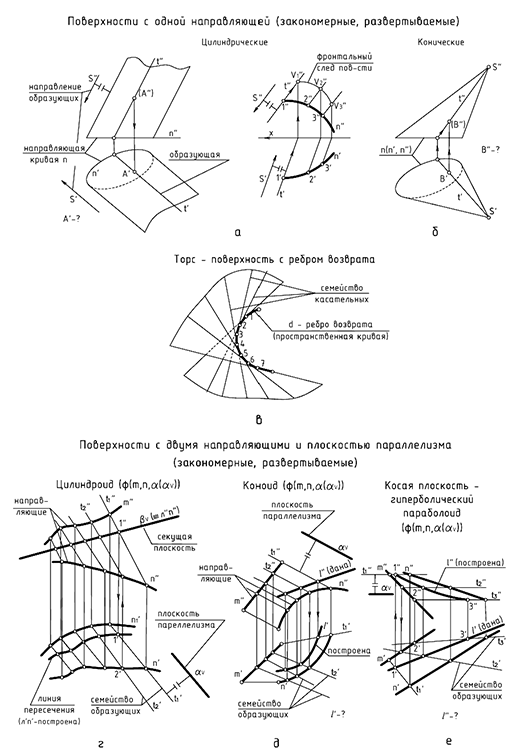
Поверхности линейчатые развертываемые.

1.1. Цилиндрическая поверхность. Образуется движением прямой линии 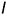по криволинейной направляющей 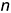и остающейся во всех своих положениях параллельной некоторой заданной прямой линии 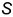(рис. 11.9).

1.2 .Коническая поверхность. Образуется движением прямой линии 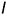по криволинейной направляющей и проходящей во всех своих положениях через некоторую неподвижную точку 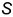, называемую вершиной конической поверхности (рис. 11.10).

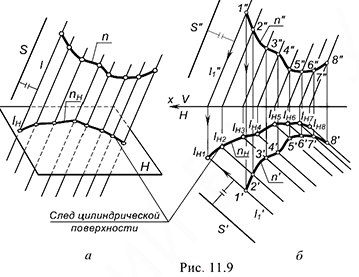
Линия, получаемая при пересечении цилиндрической или конической поверхностей с плоскостью, называется следом поверхности. На рис. 11.9, а и рис. 11.10, а показаны следы этих поверхностей в пространстве.

На рис. 11.9, б показано построение на чертеже горизонтального следа 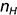цилиндрической поверхности посредством семейства произвольно задаваемых образующих 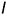, параллельных прямой 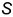, определяющей их направление. След построен по точкам являющимся горизонтальными следами образующих.

Для построения недостающих проекций точек, принадлежащих цилиндрической или конической поверхности, также используют их образующие.

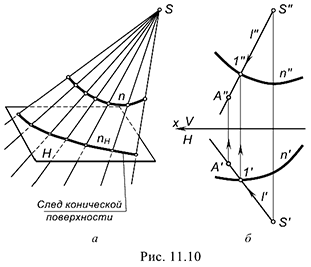
На рис. 11.10,6 показано построение недостающей фронтальной 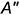проекции точки 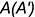посредством промежуточной образующей 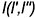. Вначале строят ту проекцию образующей 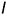, на которой находится заданная проекция 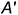точки, то есть в данном случае — горизонтальную проекцию .

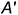Затем, используя точку пересечения 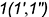этой образующей с направляющей кривой линией 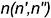, строят фронтальную проекцию 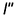образующей, и посредством линии связи находят искомую недостающую проекцию точки .

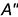1.3. Поверхность с ребром возврата (торсовая). Образуется непрерывным движением прямолинейной образующей 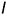, во всех своих положениях касающихся некоторой пространственной кривой 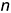. Эта пространственная кривая является для данного типа поверхностей направляющей. Ее называют ребро возврата.

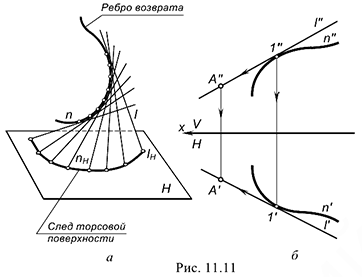
На рис. 11.11, я торсовая поверхность показана в пространстве и показан ее след 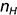как линия пересечения поверхности с некоторой горизонтальной плоскостью 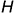. На рис. рис. 11.11, б приведен чертеж торсовой поверхности и показано построение недостающей горизонтальной проекции 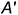принадлежащей ей точки 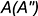. Для построения использовалась образующая 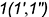, задаваемая через заданную проекцию точки 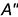касательно к ребру возврата поверхности в точке 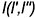. 2. Поверхности линейчатые неразвертываемые. 2.1. Поверхности с плоскостью параллелизма.

Цилиндроид и коноид — это поверхности, образованные движением прямолинейной образующей по двум направляющим, и остающейся во всех своих положениях параллельной некоторой заданной плоскости, называемой плоскостью параллелизма. В качестве плоскости параллелизма может задаваться некоторая проецирующая плоскость (ее след указывается на чертеже, рис. 11.12) или оговаривается, что плоскостью параллелизма является одна из плоскостей проекций (рис. 11.13).

Всякая плоскость, параллельная плоскости параллелизма, пересекает цилиндроид или коноид по прямой линии — по образующей. Это свойство используется при решении задач.

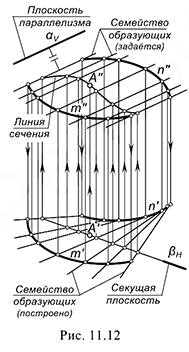
На рис. 11.12 показано построение недостающей фронтальной проекции точки 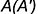на поверхности цилиндроида, заданного двумя направляющим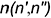и и 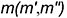и фронтально-проецирующей плоскость 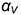в качестве плоскости параллелизма. Поскольку применить выше рассмотренный алгоритм, когда было достаточно воспользоваться одной из образующих, в данном случае не представляется возможным (не известно, как будет направлена образующая через заданную проекцию 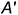точки), необходимо вначале построить семейство образующих, задавая их фронтальные проекции параллельно следу плоскости параллелизма 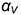(согласно закону образования поверхности цилиндроида). Построив обе проекции каркаса цилиндроида из образующих, выполняют его сечение произвольной горизонтально-проецирующей плоскостью, проходящей через заданную проекцию 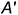точки. Затем строят фронтальную проекцию линии сечения и на ней посредством линии связи находят искомую проекцию 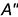точки.

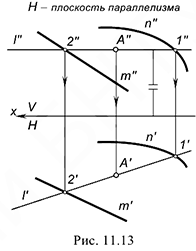
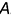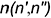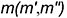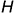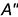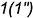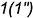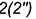На рис. 11.13 показано построение недостающей горизонтальной проекции точки принадлежащей поверхности коноида, заданного кривой и прямой направляющими и плоскостью параллелизма, в качестве которой служит горизонтальная плоскость проекций . Для этого через ее заданную проекцию построена фронтальная проекция образующей коноида, занимающая горизонтальное положение. Затем по точкам пересечения и образующей с направляющим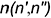и и 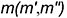построена горизонтальная проекция 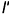образующей и на ней посредством линии связи найдена искомая горизонтальная проекция 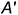точки.

Гиперболический параболоид (косая плоскость) образуется движением прямолинейной образующей по двум скрещивающимся прямым направляющим параллельно некоторой плоскости параллелизма. Эту поверхность называют также линейчатым параболоидом.

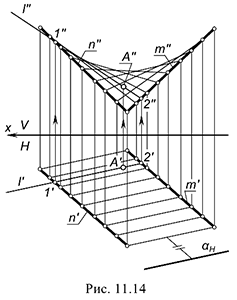
На рис. 11.14 приведен чертеж рассматриваемой поверхности в виде каркаса из образующих. Поверхность задана двумя скрещивающимися в параллельных плоскостях прямыми направляющим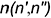и и 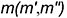и горизонтально проецирующей плоскостью параллелизма он. Там же показано построение недостающей фронтальной проекци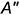и точки 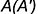, принадлежащей поверхности. Построение выполнено посредством образующей 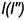для чего через заданную проекцию 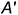вначале построена горизонтальная проекция 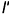образующей. Затем по точкам 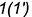и 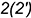ее пересечения с направляющими строят фронтальную проекцию образующей и отмечают на ней посредством линии связи искомую проекцию 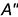точки.

Название рассмотренной поверхности «гиперболический параболоид» связано с тем, что ее фронтальный очерк (касательная кривая к фронтальным проекциям образующих) представляет собой параболу (рис. 11.6). Такую же форму имеет и профильный очерк данной поверхности. Кроме того, линия сечения данной поверхности горизонтальной плоскостью имеет форму гиперболы (форму гиперболы имеет также горизонтальный след поверхности, который можно построить, если найти горизонтальные следы ее образующих).

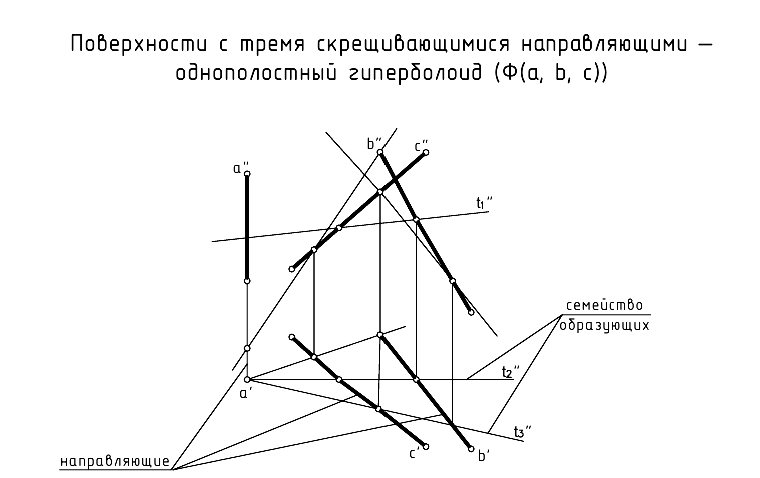
Поверхность с тремя направляющими — однополостный гиперболоид.

Эта линейчатая поверхность образуется при перемещении прямой образующей по трем скрещивающимся прямым направляющим, не параллельным одной плоскости. В частном случае линейчатая поверхность с тремя направляющими пересекается плоскостью по гиперболе; отсюда и произошло ее название — однополостный гиперболоид [23] (однополостный гиперболоид вращения, как частный случай поверхности, может быть получен вращением гиперболы вокруг ее мнимой оси или вращением прямой линии вокруг скрещивающей с ней оси).

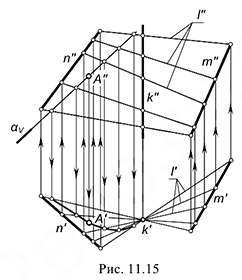
На рис. 11.15 приведен чертеж фрагмента линейчатой поверхности с тремя направляющим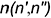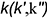и , и 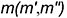. Там же показаны построения для определения положения недостающей проекци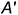и точки .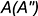

Воспользоваться для этого одной из образующих в данном примере не представляется возможным, так как неизвестно положение ее фронтальной проекции, проходящей через заданную проекцию 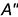точки. Зато благодаря проецирующему положению направляющей 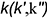можно задать горизонтальные проекции любых образующих. Воспользуемся этим и построим горизонтальную проекцию каркаса поверхности из семейства образующих 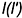. Затем по точкам их пересечения с горизонтальными проекциям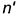и и 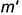направляющих построим фронтальные проекции 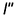этих образующих. Далее выполним сечение поверхности фронтально-проецирующей плоскостью 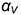. По фронтальным проекциям точек ее пересечения с образующими построим горизонтальную проекцию кривой линии этого сечения и на ней посредством линии связи определим положение искомой проекции 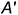точки.

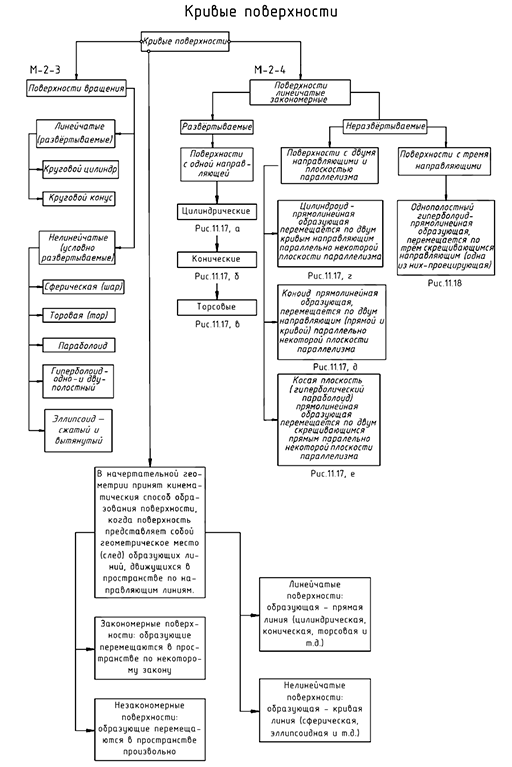
Структуризация материала одиннадцатой лекции в рассмотренном объеме схематически представлена на рис. 11.16 (лист 1). На последующих листах 2 и 3 приведены иллюстрации к этой схеме, компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 11.17 и 11.18).

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

 Начертательная геометрия для 1 курса

Возможно эти страницы вам будут полезны:

Плоские и пространственные кривые линии

Цилиндрические и конические винтовые линии

Касательные плоскости и нормаль к поверхности

Пересечение линии с поверхностью