Оглавление:





Критерий устойчивости Гурвица
Вернемся к линейной однородной системе дифференциальных уравнений. Отметим, что сложность изучения устойчивости решений в таких системах также связана с тем, что в целом корни характеристических уравнений высшего порядка довольно трудно найти.
- Разработан специальный метод, который может определять устойчивость линейных систем без решения характеристических уравнений. Выводы, сделанные этими методами, называются критериями устойчивости.
Прежде чем продолжить эти исследования, мы подтверждаем, что устойчивость стационарной точки линейной системы может быть учтена наряду со стабильностью стационарной точки линейного однородного дифференциального уравнения n-го порядка вида. Конечно, как показано в лекции «Нормальная система дифференциальных уравнений», это уравнение можно выразить как линейную однородную систему дифференциальных уравнений n-го порядка. Чтобы получить такую систему, достаточно ее заменить.
Приложение показывает, что характеристическое уравнение матрицы и гетерогенное уравнение одинаковы и поэтому имеют одинаковые корни.
Общее решение системы с матрицей — это все в виде вектора-столбца различных полиномов, и в общем случае комплексный корень характеристического уравнения является характеристическим полиномом матрицы A. Первый компонент решения является общим решением уравнения и поэтому может быть описан как первый компонент вектора, каждый из которых представляет собой вектор.
Обратное также верно. Однородная линейная система n-го порядка может быть сведена к однородному линейному уравнению n-го порядка с тем же характеристическим уравнением, что и исходная система. Кроме того, общее решение системы имеет вид, и решение описанного выше однородного уравнения n-го порядка описывается так же, как и решение. Как и в случае двумерных систем, легко получить оценку модуля решения и для отрицательной вещественной части корня характеристического уравнения сделать вывод об устойчивости соответствующего уравнения и точки покоя системы.
Также легко увидеть, что все решения, перечисленные в этом случае, стремятся к нулю. Это имеет место для многочленов в этих условиях. Следовательно, асимптотическая устойчивость сохраняется.
В то же время, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, эти пределы равны бесконечности, поэтому все решения неустойчивы. Поэтому часто говорят, что сам характеристический многочлен стабилен независимо от того, представляет ли он линейную однородную систему или одно линейное однородное уравнение.
Здесь мы рассмотрим особый способ проверки устойчивости характеристического полинома, который не требует вычисления корней полинома, на основе характеристик коэффициентов. Сделайте все коэффициенты теоремы характеристическими полиномами вещественными.
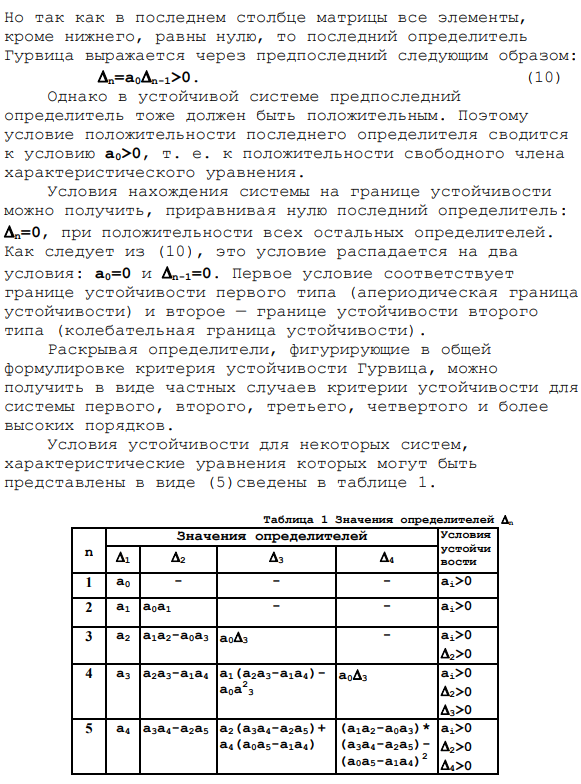
Чтобы этот многочлен был устойчивым, необходимо и достаточно, чтобы все основные диагональные миноры матрицы Гурвица были положительными.
- Исследовать устойчивость статического уравнения. Решения. Матрица Гурвица может быть построена непосредственно из заданных дифференциальных уравнений, поэтому не записывайте характеристический полином. Найти основной диагональный минор этой матрицы.
Приложите матрицу под прямым углом. Следовательно, точка покоя асимптотически устойчива. Результат Если хотя бы один главный диагональный минор матрицы Гурвица положителен, остальная точка неустойчива. Замечания. В некоторых случаях характеристический полином не является устойчивым.
Смотрите также:
Решение задач по теории автоматического управления

