Критерий Коши существования предела функции.

Оглавление:

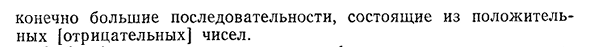
Критерий Коши существования предела функции.

Критерий Коши для существования пределов функций. Для определенности рассмотрим подробно случай предела функции y=7 (x)<в точках a, введенных определениями 1 и 1. Функция y=((x)

удовлетворяет l O b и y KOs в точках a, а для любого положительного числа e аргументы x ‘и x ‘»»удовлетворяют условию 0< / x’ — a / ему придается неравное значение). ((x’) — N x»)\416 Глава 3. Теория пределов 3.20 К Р и Тер и й Кош и с у С Ч Е С Т В О В А Н И П Р Е Д Е Ф Н К К

и в то’чке а). Для того чтобы функция d=^(x) имела конечный предел в Людмила Фирмаль

точке a, необходимо и достаточно, чтобы функция Y=} (x) удовлетворяла условию Коши в точке a. Д О К а з а т е л ь с Т В О. 1) потребность. Пусть T/(x)=6 с конечным пределом. По определению ограничения 1функции Коши для положительного числа e / 2, два значения аргументов x ‘и x» удовлетворяют условиям 0< / x’ — a / <6, 0< / x» — a|<6. для неравенства функции lc модуль определяется

неравенством (3.62).、 1/(х’)-/(х»)1= / т-б]+[в — О] К Это связано с тем, что функция y= / (x) возвращает точку a. 2) Коши означает соответствие требованиям. Так что функция^(x) удовлетворяет условию Коши•a.it необходимо доказать, что функция |(x)имеет предел до некоторой точки. Пусть{CP} — любая последовательность значений аргументов,

сходится к a и состоит из чисел, отличных от a. 1. определение предела Гейне допускает все последовательности, в которых соответствующая последовательность значений функции {/(x»)} сходится к числу B, и это число b сходится к числу, отличному от A{XP}. Во-первых, для каждой последовательности сходимости

значений аргументов{CP}, отличной от a, мы докажем, что соответствующая последовательность значений функции {/(XL)} сходится к определенному пределу. Последовательность{XP}сходится к a, и для этого условия 6>0 XP^=a, 0< / x»-a / Oo и предела при X — > +Oo. В приведенном выше определении формулировка условия Коши заменяет условие (3.60) в случае правого[левого]

предела точки a и условие aместо условия oo [oo], x»>8 [x’<-8, " x<-6]. Связанная ссылочная задача Коши доказана для схемы Людмила Фирмаль

доказательства теоремы 3.20:она просто означает последовательность значений аргументов, которые находятся во всех аргументах 3. Теория пределов Конечная, большая последовательность положительных [отрицательных] чисел.

Понятия переменной величины и функции	Почленное интегрирование степенного ряда
Предел функции по Гейне и по Коши	Почленное дифференцирование степенного ряда