Оглавление:
Ответ на вопрос о существовании решений системы линейных уравнений и о количестве возможных решений дает следующая теорема:
Теорема Кронекера-Капелли (критерий совместности системы линейных уравнений):
Система линейных уравнений с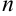 
неизвестными совместима тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы:
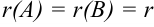, причем
- если
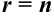(ранг матрицы равен числу неизвестных), то система имеет единственное решение; - если
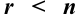(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
Пример №4.3.
Найдите все решения системы линейных уравнений:
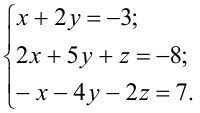
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-2) и сложим ее со второй строкой:
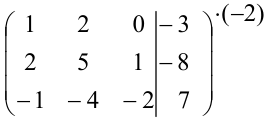
Сложим первую и третью строки:
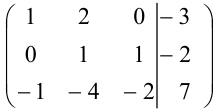
Домножим вторую строку на 2 и сложим ее с третьей строкой:
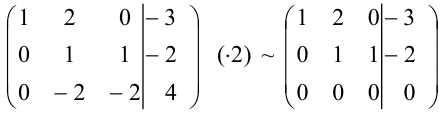
Вычеркнем нулевую строку:
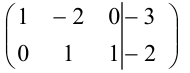
Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум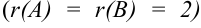 
. Следовательно, в силу критерия Кронеккера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (3), то система имеет бесчисленное множество решений. Найдем эти решения.
Восстановим систему уравнений, равносильную исходной:
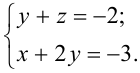
Пусть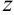 
— свободная переменная, которая может принимать любые числовые значения. Выразим 
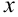и 
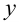через :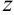
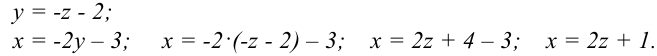
Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: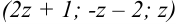 
.
Чтобы найти любое частное решение системы, достаточно в качестве 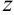взять любое действительное число.
Например, пусть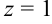 
, тогда тройка чисел (3; -3; 1) будет являться решением исходной системы.
Если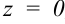 
, тогда тройка чисел (1; -2; 0) также будет являться решением исходной системы. И т.д.
Ответ: .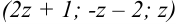
Пример №4.4.
Докажите, что система линейных уравнений не имеет решений:
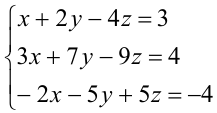
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-3) и сложим ее со второй строкой:
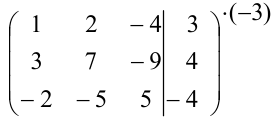
Домножим первую строку на 2 и сложим ее с третьей строкой:
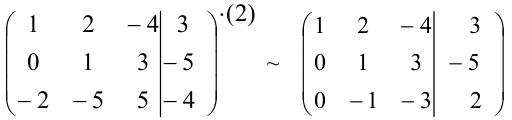
Сложим вторую и третью строки:
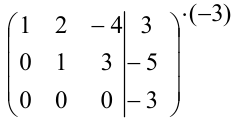
Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронеккера-Капелли, система не имеет решений.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
