Критерий Коши сходимости несобственных интегралов

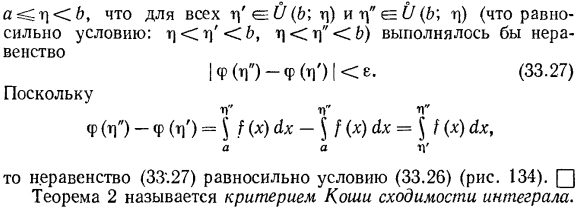
Критерий Коши сходимости несобственных интегралов

Критерий Коши сходимости несобственных интегралов. Теорема 2.О сходимости интегралов Но… Для любого e 0 число r)= r) (e), a = ^ r]; достаточно для существования. Р)Д] Б, г)д)» б, тогда Д） » ^ /(х), Ух е.(33.26） 11 ′ Φ (η)=^! (х) & х ^ б л Рисунок 134 ^ 1} ’ т) н х; + ОО. Тогда Интеграл сходится§/(x) dx, то есть、 Но… Предел (33.1) означает наличие предела P (t). м + б По критерию Коши, для существования конечного предела функции φ ^® для r)-•b, проколотого с левой стороны относительно e 0 окрестности V(b \ r])= {x.

Отметим, что из сходимости несобственного интеграла не вытекает даже ограниченность подынтегральной функции. Людмила Фирмаль

• It необходимо и достаточно присутствовать. г) х б) было такое число% точек Б, т. е.、 Пятьсот тридцать а \ ^ м. во-вторых, μ ’ эо(б \ р]) и Г «Е 0(б \ м) (равные условия. G] m]’ b, m) m)»; B) выполняется неравенство Если(l’) Ф (l ’)I e(33.27） С Ф (тг) Ф(ТГ)= 5 НХ) ух 1} » п」 ^ {(х)ух = )}(х)ух、 Но… Но… П ’ § 33.Частичный Интеграл. Неравенство (33.27) эквивалентно условию (33.26) (рис. 134).

Теорема 2 называется критерием Коши сходимости интегралов. Людмила Фирмаль

Смотрите также:

Предмет математический анализ

Формулы интегрального исчисления для несобственных интегралов.	Абсолютно сходящиеся интегралы.
Несобственные интегралы от неотрицательных функций.	Исследование сходимости интегралов.