Оглавление:





Краевые условия
- Сначала должна быть выполнена требуемая функция, которая направлена на отображение изображения пространственного и временного распределения температуры. Иначе вообще невозможно добиться соблюдения законов сохранения энергии. Однако, из смысла дифференциального уравнения. Однозначного определения функции по-прежнему недостаточно. Дифференциальное уравнение показывает, как изменения температуры во времени в какой-то момент времени зависят от характеристик поля Рядом с этой точкой и находится производительность источника тепла. Это означает установить только связь между пространственными и временными изменениями. Температура.
Поэтому, чтобы найти само распределение температуры, 1)вам нужно установить каждую точку в поле Начальное состояние, из которого следует отсчитать положительные и отрицательные изменения, и 2) элемент пространства на границе поля(т. е.、 Знать природу этих эффектов (точку, в которой свойства поля непосредственно определяются внешними воздействиями). В математическом понимании искомое уравнение Где, 5, m), C-координаты любой системы. Это уравнение дает диаграмму распределения переменных 8 в 4-мерной области. За уникальность решения задач Необходимо знать совокупность условий на границах рассматриваемой пространственно-временной области.
Когда жидкость заключена между двумя вертикальными стенками, естественно ожидать, что высота стенок является важным геометрическим параметром, как и расстояние между ними. Людмила Фирмаль
Такая ситуация в математической физике, такие условия. Принято называть краевую задачу-граничным условием, которому помимо дифференциального уравнения должно быть удовлетворено и все решение задачи a. временное граничное условие состоит в определении скалярной функции точки& = F (5,■>), С)= F ®, которая указывает на распределение температуры в конкретном moment. It есть Распределение температуры можно установить как непрерывное или непрерывное, совершенно произвольное. Чаще всего задача заключается в определении температурного поля в нем Последующее развитие. В принципе, эта проблема всегда разрешима, но в современной математике не всегда возможно найти решение.
Но можно задать и другой вопрос: откуда берется это распределение температуры из предыдущего распределения? Конкретный курс развития В обратном порядке температурного поля (от настоящего к прошлому) это в конечном итоге приводит к постоянно прерывистому распределению температуры. Начнем с В этот момент дальнейшее рассмотрение процесса изменения температуры теряет свой смысл. Вопрос о предыдущем состоянии поля в книге не рассматривается. Потому что、 Вообще говоря, теория, функция、 B.
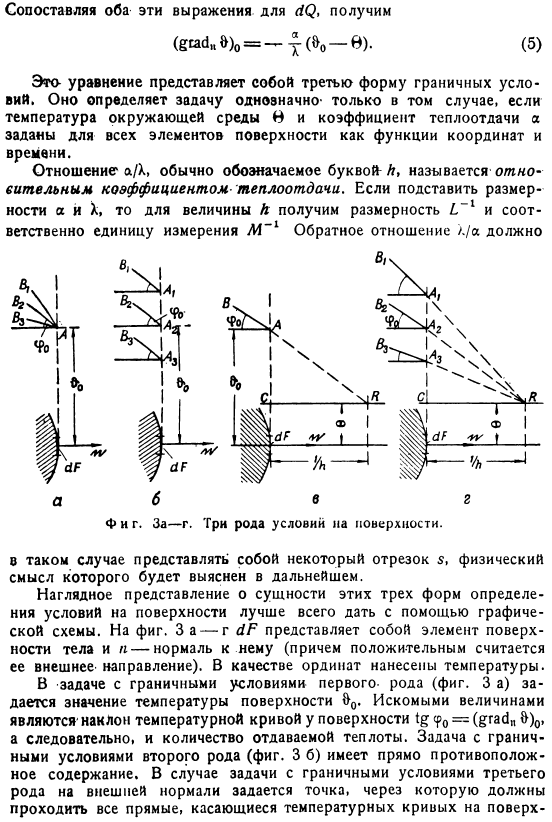
Пространственные граничные условия (граничные условия). в теории краевых задач математической физики известны 3 формы определения граничных условий. Все эти 3 формы важны. Особенно для теории теплопроводности. Первое граничное условие состоит в том, чтобы установить распределение температуры поверхности, ограничивающее температуру 1>дополнительную информацию см. В разделе Enzykl. д. Математика. Wlss. Ts a, 7c. S, S. 564-565; V. 4, S. 177-178. Поле как функция координат и time.
В этом случае необходимо установить температуру во всех точках поверхности. Эта функция полностью произвольна и может быть непрерывной или Разрывы в пространстве и времени. Однако в этой книге температура поверхности остается постоянной, или Меняйте его регулярно Граничное условие 2-го рода состоит в задании теплового потока через каждый элемент поверхности-в данном случае как функции координат и времени. Эта функция также Она отдается всей поверхности и в то же время совершенно никаким образом. Наконец, граничным условием 3-го рода является задание температуры окружающей среды и установление закона теплопередачи между поверхностью и средой тела.
- Способ теплопередачи (Или передача тепла) будет обсуждена более подробно позже в разделе book. В этом случае теплообмен следует очень сложному закону, но математически По какой-то причине мы вынуждены ставить очень простые законы на основе нашего рассмотрения. Закон охлаждения Ньютона принят в математической физике как такой закон. Суть в этом Проявлением этого закона является количество тепла DQ, выделяемое непосредственно от поверхности элемента DF температуры&С в течение времени dt в окружающую среду температуры A Поскольку разность температур EO-H пропорциональна величине dF и dt, она выражается следующим уравнением: / 2кв == а («₀- центр») dFdt.
Коэффициент пропорциональности a называется коэффициентом теплопередачи 1.Это чисто эмпирическая сумма. (В физической литературе это название. вы также можете найти внешние Теплопроводность.«Это может привести к ошибочному мышлению. Если мы подставим размеры dQ, Oo, A, dF, dt в последнее уравнение, то размеры a. Is найдено в виде[a]=. Q£,» * T «* 0 » 1.Таким образом, блок является Тепловое излучение dQ от поверхностного элемента dF должно подаваться изнутри через теплопроводность. Поэтому это количество тепла можно выразить следующим образом: Нормальные компоненты градиента температуры измеряются в непосредственной близости от поверхности.
Однако когда этот параметр достигает величины около 1700, возникает своеобразный случай свободно-конвективного потока, который можно наблюдать на. Людмила Фирмаль
По, выражение(2) может быть записано в виде: И имя тоже. Коэффициент теплопередачи.* — Прим, перев. если вы сравните оба этих выражения в dQ, вы получите: Это уравнение является 3-й формой граничного условия. Четко определите задачу только в том случае, если: Температура окружающей среды и коэффициент теплопередачи a определяется как функция координат для элемента поверхности icex、 Время. Обычно отношение A / X, обозначаемое буквой A, называют относительным коэффициентом теплопередачи.
Подставляя размеры a и X, получаем размерность L-l для величины A、 Соответственно, единица измерения M — ’ обратное отношение X / a Тоже фигура. Для-г. 3 вида состояния поверхности. В данном случае он представляет собой несколько сегментов, физический смысл которых станет ясен в будущем. Для наглядного представления сущности этих 3-х форм, определяющих состояние поверхности, лучше всего использовать графические схемы.
Рисунок 1 over-g dF-это элемент. Поверхность тела и n перпендикулярны ей (кроме того, ее внешнее направление считается положительным).Температура отображается в виде вертикальной координаты. Задача граничных условий типа 1 (3a) задает значение температуры поверхности 3₀.Требуемой величиной является наклон температурной кривой поверхности кривой tgcp. =(град»&)₀, следовательно, количество передаваемого тепла. Задача о граничных условиях типа 2 (Рис. 3 Б) имеет прямо противоположное содержание. Если есть проблема с 3-й вид граничного условия внешней нормали определяет точку, через которую проходят все прямые, касательные к температурной кривой на поверхности.
Эта точка, называемая направляющей точкой, равна X / a = 1 / A = s от surface. In в этом случае, как температура поверхности, так и количество тепла Оставьте элементы. Следующий расчет позволяет найти значение направляющей точки и определить ее местоположение. Напишите выражение (b) в виде 。 ПТ Или в принятых спецификациях Таким образом, приведенное выше рассуждение о точке направления состоит в том, что AC =9₀-0 и CR = s = i. справедливо для /a.
Если точка R выбрана в соответствии с этими Как правило, касательная температурной кривой в точке А всегда проходит через направляющую point. In во всех остальных отношениях процесс выравнивания температуры Это может происходить совершенно случайно(см. Рис. 3).в дальнейшем используйте это свойство направляющей точки неоднократно(например, см. стр.
Смотрите также:
| Температурное поле и поле теплового потока | Вводная задача |
| Вывод дифференциального уравнения Фурье | Об отыскании частных решений |

