Оглавление:




Косвенный метод наименьших квадратов (КМНК)
- Косвенные наименьшие квадраты (CMNC) Как мы уже видели, параметр а и Как я объясняю, уравнение функции потребления p дает необъективную оценку Он признается как общая переменная и частично зависит от и. Принять дальнейшие меры Times (11.5), упрощенная форма уравнения для переменной C Модель.
- Это уравнение можно выразить как: C, = a ‘+ p’ /, + и ‘„(11.8) Где a ‘= a / (1-P), P’ = p / (1-P) и u ‘= u / (1-P). При оценке параметров с использованием данных C и / значения Уравнение (11.8), проблема смещения, порожденного одновременными уравнениями Никакой грязи не будет. Пояснительной переменной является сумма инвестиций .
Поскольку это экзогенно, в результате и, наконец, Случайный член удовлетворяет четвертому условию Гаусса-Маркова. Людмила Фирмаль
Если вы оценили (11.8) с помощью OLS и получили следующее: bg = a ‘+ b’1 n (11,9) Далее «оценка без смещения», «P» b. Возвращаясь к исходному виду уравнения, вы можете получить оценки a и b. Параметры а и р. Учитывая определение a и P’b (11.8), мы можем выразить a’i b ‘. Через а и б следующим образом: °, = D и *, = D- (плоскость> Если a и b выражены как a’i b, это становится следующим. a = £ b- и * = T77- <11L1>
Потому что одно выражение a и b может быть получено путем оценки ki a’i b \ уравнение называется однозначно определенным (идентифицируемым). В следующем разделе мы рассмотрим случай, когда уникальное приобретение невозможно Начальные значения a и b и такие уравнения называются неопределившимися (Не может быть идентифицирован) и не может получить.
Для переопределенных (переопределенных) уравнений. 327 случай Монте Предположим, что функция фактического потребления Карло отображается в следующем виде: C = 100 + 0,75U + W (H.12) Случайный член в 50 раз больше случайного числа, полученного из Образец нормального распределения, ожидание ноль И единица стандартного отклонения.
Значения C и Yt взяты из уравнения Утверждения вида (11.3) и (11.5) выше, в этом случае Дисплей: С = 400 + 3 /, + 4i (11,13) Y = 400 + 4 /, + 4ig (11,14) Возьмите 20-летний период и сделайте объем легким Сумма инвестиций составляет 200 в первый год и увеличивается на 10 в следующем году Он достиг 390 за 20 лет. Оценить уравнение C для регрессионной зависимости Используя OLS от K, вы получаете: 6 = -8 4 + 0,87 U; D2 = 0,99. (11.15) (С.о.) (38) (0,02)
- Как видите, оценочный результат p слишком велик по сравнению с ожидаемым Мой смысл. Оценка в целом имеет противоположный знак. Посмотрим, как полученный результат соответствует выражению (11.4) Для смещения больших образцов. Var (/) = значение 3325 и \ = 2500, Таким образом, для большой выборки 1 B-> 0,75 + (от 1 до * ™ *} ™ = 0,75 + 0,11 = 0,86 (11,16) 3325 + 2500
Как видите, в данном конкретном случае оценка с небольшой выборкой Очень близко к значению, полученному с большой выборкой. В настоящее время KMNK используется для тех же данных. Уравнение регрессии C из 7 можно оценить как: 6 = 1 6 7 + 3,84 /, L2 = 0,53. (11.17) (С.о.) (258) (0,86) Используйте (11.11), чтобы получить функцию потребления 6 = 34 + 0,7 9 G, (11,18)
Это ближе к истинной модели. Людмила Фирмаль
Тем не менее, вы можете продолжить Подозреваю преимущества CMNC Коэффициент R1 (0,53 вместо 0,99) и большая стандартная ошибка. Однако высокое значение коэффициента L2 в исходном уравнении 1 Предполагается, что значение Var (/) остается постоянным для большой выборки. Это вер Но, например, если сумма инвестиций является одной из последних 20 в ближайшие несколько лет Ведущее значение с равной вероятностью.
Не следует избегать. Даже если между C и Y нет экономической связи, Получить большое значение коэффициента L2 при создании уравнения регрессии Причиной зависимости C от Y является Потребление составляет значительную часть общего дохода и прибыли Разница между C и D не сильно отличается от регрессионной зависимости C от C.
Для стандартной ошибки в любом случае, нарушение условий Гаусс-Марков рассчитан неверно. Когда определено 99% Доверительный интервал для b с использованием оценок и стандартных ошибок Ку был приобретен на основе (11.15), но без рассмотрения вопроса, Вы можете обнаружить, что этот интервал не включается из-за смещения Фактическая стоимость.
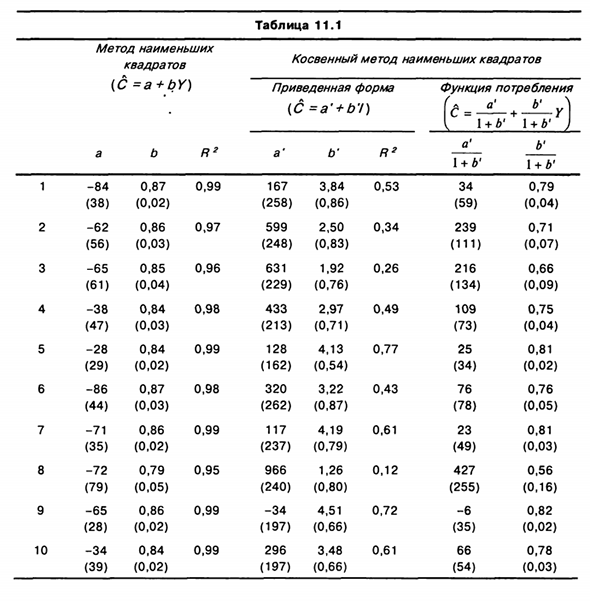
Конечно, это слишком быстро, чтобы сделать такое обобщение, основанное на одной вещи Природный эксперимент. В таблице. 11.1 показывает результаты эксперимента Эксперимент с 10 различными наборами случайных чисел для 20 наблюдений С переменными. Левая сторона стола. 11.1 показывает результат построения уравнения Регрессия между Cs X с использованием OLS.
Оценка указана в центре таблицы. Для заданной формы регрессионно-зависимое уравнение для C /. Справа Часть таблицы, полученная из средней части Учитывая соответственно Расчетная функция потребления получена с использованием CMNC. Анализ таблицы Цы показывает, что оценки, рассчитанные на основе CMNC, почти всегда лучше.
Оценка на основе наименьших квадратов и оценочного значения параметра наименьших квадратов близка к значению Его можно получить из уравнения (11.16). упражнения 11,4. У двух исследователей есть следующая простая модель Получение дохода может применяться для учета некоторых закрытых экономик. C, = cc + pG, + // ,; Y = C, + / „ Где Y, C к I — соответственно общий доход, потребление и инвестиции.
На самом деле, случайные члены. Используйте одинаковые временные ряды для Y и C И / или исследователь построил зависимое от регрессии уравнение для C Регрессионная зависимость Y от /, другие- / Результат: 6 = 4120 + 4,0 /; фран = 4120 + 5,0 /, Покажем, что оба подхода дают одинаковую оценку a и p. 11,5. Почему математически обосновать в предыдущем упражнении Все результаты должны быть одинаковыми.
Смотрите также:
| Смещение при оценке одновременных уравнений | Инструментальные переменные (ИП) |
| Структурная и приведенная формы уравнений | Автокорреляция и связанные с ней факторы |
Если вам потребуется помощь по эконометрике вы всегда можете написать мне в whatsapp.

