Оглавление:








Косозубые цилиндрические передачи
- Конические цилиндрические шестерни Цилиндрическое колесо, зубья которого расположены вдоль винтовой линии разделительного цилиндра, называется угловым зубчатым. В этом случае шаг спиральной линии зубьев на разделительном цилиндре имеет большое значение по сравнению с шириной коронки, а кривизна зубьев едва заметна (рис.4.32). В паре сопряженных конических колес с внешним зацеплением угол наклона зубьев относительно шин
разделительного цилиндра Р равен по величине, но противоположен по направлению. Одно колесо левое, другое правое. Копируя отрезанную винтовую шестерню (на филировальном станке) или путем двигать к таким же инструменту и шпоре(на Формирователе шестерни или резцах). Наклон зуба получают поворотом инструмента на угол P. Преимущества конических зубчатых колес следующие: высокая гладкость зацепления(более высокий угол Р);
уменьшенный шум и дополнительная динамическая нагрузка;более высокая грузоподъемность. Недостатком конических зубчатых колес является Людмила Фирмаль
наличие осевой силы Fa, которая стремится перемещать колесо вдоль оси и требует осевой фиксации оси. Конические зубчатые колеса используются в механизме* » — ing на средних и высоких скоростях. Основные геометрические параметры. Косое колесо(рис. 4.33) расстояние между зубьями может быть измерено в нормальном направлении n-n с гранью и окружностью t-t,в первом случае мы получаем окружной шаг Pt, во втором-нормальный шаг этих различных в направлении зубьев модулей: mt-Pt/n-окружность зуба модуля, т. е. линейное значение модуля зуба.- Окружность зуба 115
градусов шага; cha=RYA/p-нормальный коэффициент зубьев. Согласно рисунку. 4.33 P z=P » / cosp, следовательно mt=mrJcos$, (4.29) Где Р=8…15°(иногда до 20°). Контур косого зуба обычного сечения соответствует исходному контуру стойки инструмента, а следовательно, совпадает с контуром прямого зуба t=TYA. Обычный модуль должен соответствовать СЭВ310-75 и быть начальным значением расчета геометрических параметров. Диаметр деления и начальная окружность d=dw = mtz=mnz / cos p. Высота головки косого зуба ha и ножки hf, ha-mn; hf=-l, 25мн. Диаметр окружности на вершине да-
- д+2шя. 116º впадины DF-D-2,5 TP окружности. Расстояние до центра Od,=(di+<^a)/2=TP(zi+4-yy)/2cos p=m » zs / (2cos P). (4.30)) В конической передаче изменение величины угла p позволяет плавно изменять диаметр начального круга колеса, что позволяет более точно обеспечить стандартное значение aw. В конических зубчатых передачах осевой шаг РХ представляет собой расстояние между линией одноименного зуба смежного вращения вдоль линии пересечения грани осевого сечения зубчатого колеса и его разделительной поверхностью. Прямозубую передачу можно рассматривать как частный случай перекоса ширины колеса, где ширина колеса-p=0, Px-0 и, следовательно, t=TA=mt, P=RP=Pt-длина зуба перекоса колеса b=bw/cos p, где T = TA = mt. Эквивалентные
колеса. Сопротивление усталости при изгибе косого зуба определяется его размером в нормальном сечении. В соответствии с этим расчетом для лонжерона используются эквивалентные параметры лонжерона, полученные из следующих условий. Деление косого колеса на обычное сечение 1-1 круга(рис. 4.34) образует эллипс с полуосью a=d / 2; b=d/(2cosP). Радиус кривизны эллипса в зоне малой полуоси p,=d0 / 2=/; ba * Пожалуйста, обратитесь к курсу аналитической геометрии. д-2__. д d4cos «, потому что cos2P1 Где эквивалентный диаметр колеса d » =d / cos2p. 117. P на конце колеса (рис.
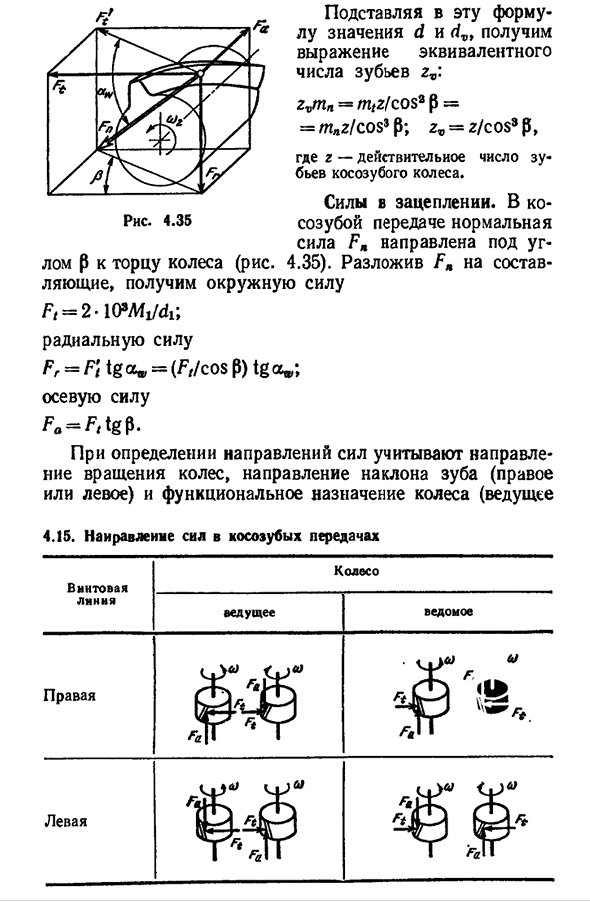
Подставляя значения d и dv в это уравнение, получим эквивалентное число zvmn=m/Z / cos2p — =maz / cos3fr, z»=z / cos3p, Где z-действительное число зубьев на косом Людмила Фирмаль
колесе. Сила взаимодействия. В косой передаче нормальная сила направлена ниже ug-4.35). При разложении ФА на составляющие, Окружная сила 6=2-lOWi / df, радиальная сила Fr=Ft tgOjp=(Ftl cos P) tga»; осевая сила Fe=F/tgp. При определении направления силы учитывают направление вращения колес, направление наклона зубьев (правое или левое) и функциональное назначение колес(привод 4.15 Наровля мощности винтовых передач Спираль Колесо Ведущий-ведомый Правильно М» * Левое крыло Тысяча, сто, восемь, семнадцать Ф. Т. ) Рис 4.36 Или раб). Осевые силы FA и окружные силы ft, зависящие от этих факторов, приведены в табли
це. 4.15 Осевая сила Fa нагружает подшипник, которая увеличивается примерно на 0, увеличивается дополнительно. Особенности косого зацепления. В отличие от прямых зубьев, зубья косой шестерни зацепляются не сразу по всей длине, а постепенно приводят к зацеплению, которое составляет несколько пар зубьев. Это уменьшает нагрузку на один из зубов. Нагрузка между зубьями распределяется пропорционально длине контактной линии/, 2, 3 (фиг. 4.36, б). По бокам косые зубья расположены под углом х, где проходит линия
соприкосновения. Эта характеристика конических зубчатых колес учитывается путем введения в Формулу расчетной нагрузки дополнительного коэффициента КНА (или кф а), учитывающего распределение нагрузки между зубьями. Вы можете написать из уравнения диагональной шестерни (4.20 1(4)1 ) К== Где-(6^ / cosfJ) VA K8-общая длина линии контакта; K e-коэффициент, y■. Изменчивость общей длины линии касания. Рассматривая формулы (4.20) и (4.21), запишем q=-wt cos P/(eea cos aw). 1194.16. Значение коэффициента И к ФА Колесо искажения может работать даже когда без ломать захват- К Заглушка ента■л СН ССР Чжоу Са о ва<1,ее предложение- Три Е Рост I.
м/с Эффективность осевого перекрытия составляет 5 10 15, er>1, где 6 1.01 1.03 1.04 0.72 Я сделал это!P K-t g s в 0 7 1.05 1.07 1.09 0.81 8 1.09 1.13 — ■0.91 Когда зуб перемещается, линия контакта перемещается в направлении от линии 1 к линии 3. В этом случае опасным положением является 1, где зубья разрушают угол (рис. 4.36, а). Усталостные трещины образуются у основания зубьев стопы в местах концентрации напряжений, а затем распространяются под углом. Нагрузка q достигает своего максимального значения в средней
линии зубов. Расчет контактной усталости активной поверхности зуба конического зубчатого колеса аналогичен расчету прямой зубчатой передачи[см. уравнение (4.24) 1-осевое расстояние направления определяется из расчетного расчета (И_. 1) / / G^1 0W, K..фут И * [Обо мне]2′ Где K a-u0, 5(2I g g e) 2S Uch e t o M коэффициент K N a;K a=>=43 МПА|/3-вспомогательный коэффициент при расчете стального косого колеса. Расчет испытания выполняется таким же образом, как и расчет прямозубой передачи[см. формулу (4.23) 1: <[О]> Здесь ZH1, 76cos0-коэффициент, учитывающий форму сопряженной поверхности зуба. Среднее значение zh » 1,71; Ze=]^i/K eea-коэффициент, учитывающий общую длину линии контакта, котора
я зависит от EA[уравнение (см. 4.12)] и K e-0,9…0,95 среднее значение Ze * = * 0,8; ZM=275 mpa1 / a; K время v-см. таблицу. 4.10; — см. таблицу. 4.9; см. Joe-table.. 4.16 Расчет зубьев на изгибную усталость. Расчет винтовых передач является эквивалентом формулы паразитной 120 переносят с введением их поправочных коэффициентов. Согласно положению прочности, общие размеры конических зубчатых колес более малы чем те из прямых зубов. Расчет конструкции. Аналогично расчету зубчатой передачи[см. формулу (4.28) 1 нормальные коэффициенты сцепления / 71,4-КТ fM M F> (Выбирается по таблице, при этом УР-это коэффициент в виде зуба. 4.14 эквивалентное число зубьев zv). Для колес с внутренними зубьями Yp можно
приблизительно определить по формуле Y p^4G/(g+20); Kt»11,2—некоторые средние значения K F v, UE и Y&. Формула (4.28) заменяет меньшее из двух соотношений, рассчитанных для шестерен и колес. Проверьте расчет. Как и при расчете прямой зубчатой передачи[см. уравнение (4.27)]учитывают (4.31)изгибное напряжение в зубе or-YpY&YP K. FbKpvKFa[o?]; О, — Уу,! Фунт» [«]. (4.32) Где UE-1 / Ke8 «- коэффициент, учитывающий перекрытие зубьев, — по гост21354-75 для конического зубчатого колеса = = * 1; ur » cos P-коэффициент, учитывающий наклон зуба. Для расчетов рекомендуется брать Ur1-p / 140. При Р=8…1 8 * УР среднее значение 0,9;КРА-см. таблицу. 4.16 расчет производится для менее прочных зубов с меньшим
соотношением[o/?] / Y/?. О / в конце концов?= = 0,9 г/?Т -^ — /( / ?РК/?1, ALH^[o/?Я не уверен. (4.33)шевронная цилиндрическая передача. Шевронное колесо представляет собой двугранное колесо, обод которого может быть выполнен целиком(рис. 4.37), и с ветвью кроны по следу. Тележка в середине колеса необходима для выхода режущего инструмента-червячной фрезы(рис.4.38). Из-за различного направления зубьев Семитронов осевая сила F J2 взаимно уравновешивается на колесе и не передается на подшипник. К этому
времени、 121 страница. 4.37 Шевронные колеса с углом зубьев Р=25…40°для того чтобы увеличить прочность зубов и передачу, ровную деятельность. Недостатком шевронных колес является высокая стоимость их изготовления. Применяйте их с мощным быстрым закрытым переносом. Геометрические и прочностные расчеты шевронной передачи аналогичны расчетам косой передачи. Для елочной передачи коэффициент ширины обода колеса равен f&W=0,4…0,8, в то время как BG 2, 5dx (прокатное оборудование допускается в 1, 25).
Смотрите также:
| Выбор материалов и допустимых напряжений | Последовательность расчета цилиндрических передач |
| Расчет прямозубых цилиндрических колес на усталость | Конические зубчатые передачи |

