Оглавление:
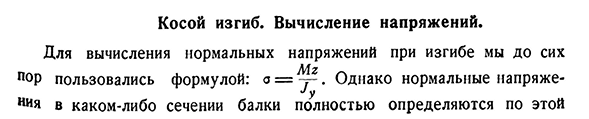






Косой изгиб. Вычисление напряжений
- Косой изгиб. Расчет напряжений. Для расчета нормального напряжения изгиба ранее использовалась формула а=. Однако нормальное напряжение определяется этой диагональю 16 * 484 YZGIV [GL] полностью на пне в любом сечении балки**/. XXVI 1) в случае только плоского изгиба, когда кривизна оси балки возникает на рабочей поверхности силы, а нейтральная ось является главной осью инерции поперечного сечения, перпендикулярной плоскости
нагрузки. На практике часто встречаются случаи, когда рабочая поверхность силы, перпендикулярная оси стержня, не совпадает ни с одной из двух поверхностей, проходящих через ось стержня и главную ось инерции- Фигура. 408. Количество поперечных сечений стержня. Опыт показывает, что криволинейная ось стержня в этом случае уже не существует на рабочей поверхности силы, и бывают случаи так называемых косых изгибов.
Крыша коробки обычно подвергается нагрузке, рабочая поверхность которой является основной осью и имеет довольно большой угол наклона(рис. 408); Людмила Фирмаль
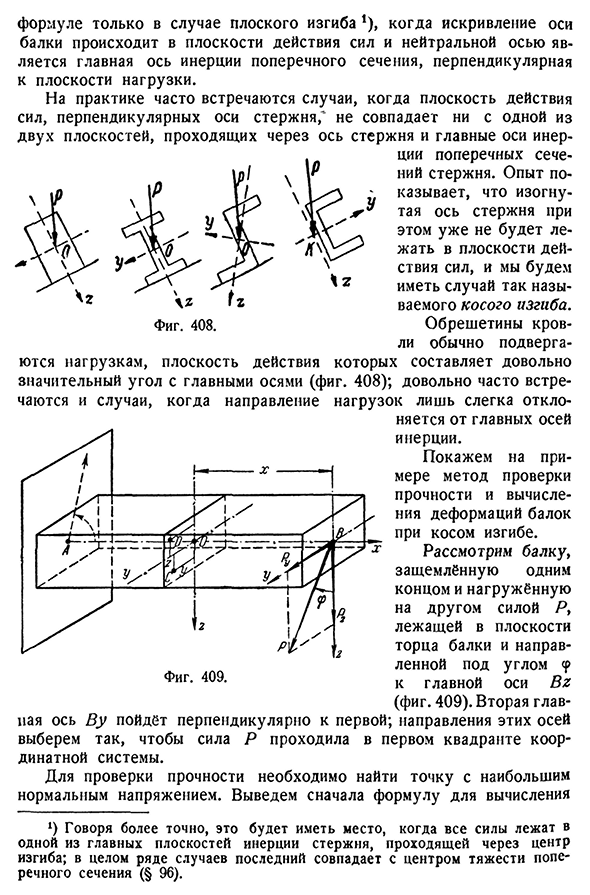
часто направление нагрузки слегка отклоняется от основной оси Фигура. 409. Инерция Покажем, как проверить прочность и рассчитать деформацию балки при косом изгибе. Балка одним концом зажата балкой торца плоскости, лежащей в силе Р, другим нагружается, направление шпинделя относительно угла СР для балки задано БЗ(фиг. 409). Направление этих осей выбирается таким образом, чтобы сила P проходила через первый квадрант системы
координат. Чтобы проверить прочность, необходимо найти точку с наибольшим нормальным напряжением. Выведем формулу для расчета первого 0 точнее, это одна из главных плоскостей инерции стержней, где все силы проходят через центр изгиба§ 157]косого изгиба. Расчет напряжения 485 Обычное напряжение в любой точке любого поперечного сечения было разнесено на расстояние х от свободного края балки. Разложим силу P на составляющие RG
- и Pyf, направленные вдоль оси инерции сечения Bz. Значение этих компонентов определяется по формуле ПЗ=р потому что СР и Ру=Р грех<п. Поэтому мы свели случай косого изгиба к комбинации двух плоских изгибов, вызванных силами Pz и Ru, расположенными на инерционной главной плоскости балки. Суммируя напряжения и деформации, соответствующие каждому из этих изгибов, мы получаем решение и для косого изгиба. Изгибающий момент сечения с абсциссой х от сил РГ и Ру будут равны /Му| — РГР=Р х с COS СР=М, потому что СР|М Г / =ру х=р х Sin СР=М СР грех. (26.1)
Изгибающие моменты ПЛО-иконок y и z в M указывают на главную ось, на которую берется момент. Применяя векторное изображение момента, можно разложить весь изгибающий момент M непосредственно на главную ось для вычисления изгибающего момента Mu и Mz 410). Для установления признаков изгибающего момента, в связи с переходом к пространственной задаче, необходимо ввести дополнительные условия, определяющие эти признаки. Теперь мы ограничимся вычислением абсолютной величины изгибающего момента, но при расчете последнего учитывается влияние направления момента на признаки напряжения.
Рассчитаем напряжение в любой точке C (координаты Y и G) в первом Людмила Фирмаль
квадранте(рис. 409). Для этой точки можно рассчитать вертикальное напряжение, вызванное отдельно моментом Mu и MG изгиба балки в главной плоскости XZ и XX. Нормальное напряжение в точке C от момента изгиба m v является сжимающим (отрицательным), а уравнение 486-косым изгибом[CH. XXVI — c o s f » g d e L-момент инерции относительно оси y, которая является нейтральной осью при изгибе Mumm. В этот момент Mz вызывает тоже равное сжимающее напряжение — sin CP; JZ-момент инерции секции ЮЖД ЮЖД ось z найдена как алгебраическая сумма напряжений, при которых получено полное напряжение в точке C: 0= = + (26.2) J y J Z / В этом случае можно использовать эту формулу для расчета напряжения
в любой точке каждого участка балки. Эта формула выводится для точек с положительными координатами y и z, и подстановка значений координат с соответствующим знаком всегда дает правильные символы напряжений в соответствии с формулой (26.2). Поэтому о точке D (рис. 409) координата y положительна, а z-отрицательна, и в соответствии с этим первый член формулы (26.2) является положительным (растягивающим) напряжением, а второй-все еще сжимающим. Формула (26.2) учитывает частный случай косого изгиба балки, которая накладывается на один конец и нагружается концентрацией р на другом конце, но это легко
заметить, в противном случае для балки, которая нагружается и фиксируется, необходимо согласовать правила маркировки. Если положительное направление центральной оси основной инерции балки всегда выбирается таким образом, чтобы след рабочей поверхности силы в сечении проходил через первый квадрант, то, справа от уравнения (26.2), справа от уравнения (26.2), для получения правильного знака напряжения для остальных частей балки необходимо выполнить следующие действия: Для того чтобы найти максимальное нормальное натяжение, необходимо найти опасную часть балки и найти в ней самую сильную точку. Из уравнения (26.2)
видно, что опасная часть находится там, где изгибающий момент L1 достигает максимального значения. Чтобы найти опасную точку, рассмотрим, что при плоском изгибе деформация, соответствующая нормальному напряжению, сводится к относительному вращению сечения вокруг нейтральной оси. Для косого изгиба, который является комбинацией двух плоских изгибов, мы имеем диагональный изгиб§ 157]. Расчет напряжения 487 Одновременное относительное вращение секции вокруг двух осей, пересекающихся в центре тяжести секции. Из кинематики известно, что вращение фигуры вокруг двух пересекающихся осей может быть заменено вращением вокруг оси, проходящей через перекресток. Таким образом, при косом
изгибе мы в каждом сечении имеем линию, проходящую через центр тяжести, а вокруг нее происходит вращение поперечного сечения при деформации балки. Эта ось нейтральна, волокна, расположенные в ее плоскости, не удлиняются, не укорачиваются, и нормальное напряжение в точке нейтральной оси сводится к нулю. При относительном вращении сечения волокна испытывают наибольшую деформацию (растяжение или сжатие), наиболее удаленную от нейтральной оси. Таким образом, нахождение опасной точки с косым изгибом сводится к определению положения нейтральной оси и нахождению наиболее удаленной от нее точки. Уравнения
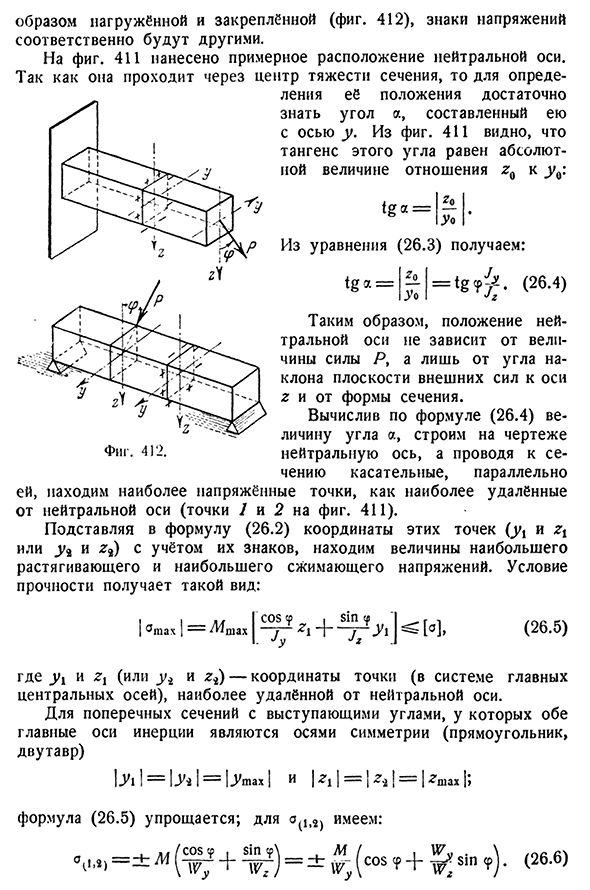
нейтральной оси выводятся из условия Z^\, которое заменяет эти значения на нормальные напряжения, обозначающие координаты этих точек, а также y и z в Формуле (26.2).: Точка на этой оси равна нулю. п __м потому что СР * Z(л грехом СР * ц0 ЮЖД — Уменьшите до W, у нас есть: потому что+ХП. G0 и грех СР * ц0 J2 в =0. (26.3) Это прямая линия, проходящая через центроид сечения (_u0=0 и zQ=0). Как использовать 411 показывает два участка балки, ось y и ось z являются главными осями инерции. Предположим, что балка нагружена согласно схеме рисунка. 409, для каждого квадранта сечения, где на каждом сечении изображена Проекция Силы Р, имеется знак вертикального напряжения; знаки под сечением выше-изгибающий момент 7, Если φ488 косой ижев[глава xxvi пути нагружен и закреплен (рис. 412), признаки стресса меняются
соответственно. Как использовать 411 указывает приблизительное положение нейтральной оси. Поскольку он проходит через центроид сечения, достаточно знать ось y и угол A, построенный ею, чтобы определить его местоположение. 411 видно, что касательная этого угла равна абсолютному значению отношения к y: Таким образом, положение нейтральной оси зависит не от величины силы P, а от угла наклона и сечения оси g внешней силы. Величина угла а, рассчитанная по формуле (26.4), строится на чертеже фигуры. 412 нейтральной оси, и делаем касательную к сечению, а параллельно ей находим самую упорную точку как самую дальнюю
от нейтральной оси (рис.7 и 2 точки). 411). Подставляя координаты этих точек (Ji и ЗТ или Y3 и G2) в Формулу (26.2), получаем значения максимальных растягивающих и максимальных сжимающих напряжений, с учетом их знаков. Требования к прочности получают этот вид: / ага! =Л/Ша х|^^±^? 1]^S>(26.5), где z x(или j2 и z2) — координаты наиболее удаленной точки (в системе главной центральной оси) от нейтральной оси. Для поперечного сечения с выступающим углом, где обе инерциальные главные оси являются осями симметрии (прямоугольник, двутавр).) / ^1 / =1l1= / нет. А|я / г|=/г * й=|.?Формула (26.5)упрощается, например:§ 157] косой изгиб. Расчет напряжения 489 Условие прочности такого сечения:|O » 13×1=^(cos? в +^/с?)<[<?Я не уверен. (26.7) при выборе раздела, необходимо установить его отношения, и, зная[а], L4t, а угол СР, она должна удовлетворять условиям прочности(26.7).
Смотрите также:
| Расчёты балок конечной длины | Определение деформаций при косом изгибе. |
| Косой изгиб. Основные понятия | Примеры расчётов при косом изгибе |

