Косой изгиб
Под косым изгибом понимается такой случай плоского изгиба, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции бруса.
Наиболее удобным способом решения задач на косой изгиб является приведение его к двум прямым плоским изгибам. Для этого возникающий в поперечном сечении изгибающий момент раскладывают на два изгибающих момента, которые действуют в плоскостях, проходящих через главные оси инерции сечения. При косом изгибе в поперечных сечениях бруса возникают в общем случае как поперечные силы, так и изгибающие моменты. Однако влиянием касательных напряжений, появление которых обусловлено действием сил 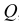 , в расчетах на прочность обычно пренебрегают.
, в расчетах на прочность обычно пренебрегают.
Рассмотрим балку, защемленную одним концом и нагруженную на другом силой 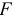 (рис. 2.50, а). Сила
(рис. 2.50, а). Сила 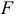 лежит в плоскости торца балки и направлена под углом
лежит в плоскости торца балки и направлена под углом 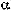 к главной оси
к главной оси 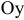 . Вычислим напряжения в некоторой точке
. Вычислим напряжения в некоторой точке 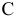 поперечного сечения, отстоящего на расстоянии
поперечного сечения, отстоящего на расстоянии 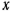 от свободного конца балки Для показанного на рисунке направления главных осей точка
от свободного конца балки Для показанного на рисунке направления главных осей точка 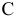 имеет положительные координаты
имеет положительные координаты 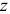 и
и 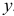 . В указанном сечении изгибающие моменты, возникающие при изгибе бруса в вертикальной и горизонтальной плоскостях (рис. 2.50, б), соответственно
. В указанном сечении изгибающие моменты, возникающие при изгибе бруса в вертикальной и горизонтальной плоскостях (рис. 2.50, б), соответственно
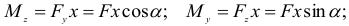
здесь 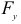 и
и 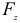 — вертикальная и горизонтальная составляющие силы
— вертикальная и горизонтальная составляющие силы 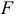 .
.
Индексы 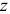 и
и 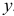 при
при 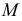 обозначатся главные оси, относительно которых действуют изгибающие моменты. Эти моменты будем считать положительными, если они вызывают в точках первого квадранта растягивающие напряжения.
обозначатся главные оси, относительно которых действуют изгибающие моменты. Эти моменты будем считать положительными, если они вызывают в точках первого квадранта растягивающие напряжения.
Исходя из принципа независимости действия сил, напряжение 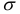 в точке
в точке  можно вычислить, рассматривая два плоских изгиба отдельно. Тогда
можно вычислить, рассматривая два плоских изгиба отдельно. Тогда
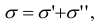
где 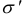 и
и 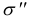 — нормальные напряжения, вызываемые действием соответственно только момента
— нормальные напряжения, вызываемые действием соответственно только момента 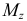 и только момента
и только момента 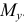 .
.
Поскольку
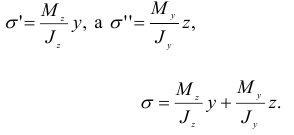
Хотя формула (2.98) получена из рассмотрения частного случая косого изгиба балки, однако она является общей формулой для вычисления напряжений при косом изгибе. Следует только помнить, что изгибающие моменты и координаты точек, в которых определяют напряжения, необходимо подставлять в указанную формулу со своими знаками.
Уравнение нейтральной линии при косом изгибе в любом поперечном сечении получим из выражения (2.98), положив 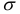 = 0 и обозначив координаты точек этой линии
= 0 и обозначив координаты точек этой линии 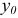 и
и 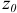 . Тогда
. Тогда
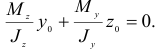
Уравнение (2.99) показывает, что нейтральная линия всегда проходит через начало координат (центр тяжести 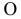 сечения). Преобразуем полученную зависимость
сечения). Преобразуем полученную зависимость
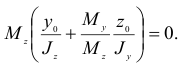
Так как 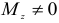 , то
, то
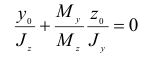
Здесь
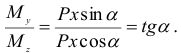
Поделив обе части уравнения (2.90), [13] на 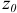 и проведя небольшие преобразования, получим
и проведя небольшие преобразования, получим
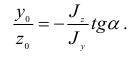
Отношение 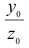 представляет собой тангенс угла
представляет собой тангенс угла 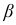 наклона нейтральной линии к оси
наклона нейтральной линии к оси 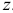 . Поэтому окончательно имеем
. Поэтому окончательно имеем
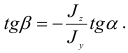
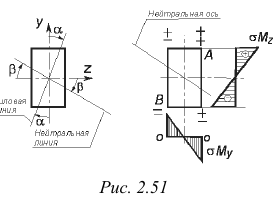
При 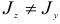 также
также 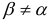 , т. е. нейтральная линия неперпендикулярна к силовой линии, как это имело место для прямого изгиба. Если же
, т. е. нейтральная линия неперпендикулярна к силовой линии, как это имело место для прямого изгиба. Если же 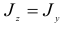 (круг, квадрат и др.), то указанные линии взаимно перпендикулярны, но в этом случае косой изгиб вообще невозможен, поскольку любая центральная ось сечения является главной осью инерции.
(круг, квадрат и др.), то указанные линии взаимно перпендикулярны, но в этом случае косой изгиб вообще невозможен, поскольку любая центральная ось сечения является главной осью инерции.
Используя зависимость (2.101) для определения положения нейтральной линии, необходимо помнить, что углы 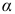 и
и 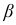 положительны, если отсчитываются следующим образом:
положительны, если отсчитываются следующим образом: 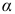 по часовой стрелке от оси
по часовой стрелке от оси 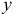 , а
, а 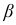 против часовой стрелки от оси
против часовой стрелки от оси 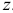 . На рис. 2.51, а показано положение нейтральной линии в опасном сечении балки, рассмотренной выше.
. На рис. 2.51, а показано положение нейтральной линии в опасном сечении балки, рассмотренной выше.
Прочность балки следует проверять в тех сечениях, где изгибающие моменты 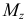 и
и 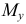 достигают одновременно больших значений. Таких сечений может оказаться несколько.
достигают одновременно больших значений. Таких сечений может оказаться несколько.
Если положение опасного сечения известно, то в нем нужно отыскать наиболее нагруженные точки. Наглядное представление о распределении нормальных напряжений по поперечному сечению балки дают эпюры 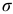 . Применительно к рассмотренной балке эти эпюры показаны на рис. 2.51, б. Очевидно, что наиболее напряженными будут точки
. Применительно к рассмотренной балке эти эпюры показаны на рис. 2.51, б. Очевидно, что наиболее напряженными будут точки 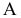 и
и 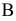 , наиболее удаленные от нейтральной линии, причем в точке
, наиболее удаленные от нейтральной линии, причем в точке 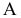 действует максимальное растягивающее напряжение, а в точке
действует максимальное растягивающее напряжение, а в точке 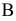 — максимальное сжимающее напряжение. Для пластичных материалов обе точки одинаково опасны. В случае хрупкого материала более опасной будет точка
— максимальное сжимающее напряжение. Для пластичных материалов обе точки одинаково опасны. В случае хрупкого материала более опасной будет точка 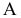 Условие прочности имеет следующий вид:
Условие прочности имеет следующий вид:
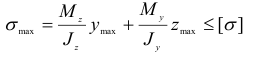
где 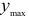 и
и 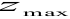 — координаты точки, наиболее удаленной от нейтральной линии.
— координаты точки, наиболее удаленной от нейтральной линии.
Для сечений, имеющих две оси симметрии (например, прямоугольник, двутавр и др.) и выступающие углы, опасной будет одна из угловых точек, для которой условие прочности можно записать так:
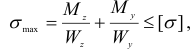
где 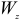 и
и 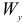 — моменты сопротивления сечения относительно осей
— моменты сопротивления сечения относительно осей 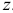 и
и 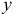 .
.
Если изгибу в двух плоскостях подвергаются брусья круглого, квадратного и тому подобных сечений, для которых косой изгиб невозможен, то их рассчитывают на прочность по суммарному изгибающему моменту. Этот момент представляет собой геометрическую сумму изгибающих моментов, действующих в вертикальной и горизонтальной плоскостях:
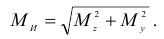
Условие прочности аналогично условию (2.59).
Определяя величину прогиба в какой-либо точке балки, вначале вычисляют прогибы 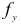 и
и 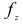 в направлении главных осей, а затем их суммируют геометрически Таким образом, полный прогиб
в направлении главных осей, а затем их суммируют геометрически Таким образом, полный прогиб
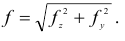
Нетрудно установить, что линия полного прогиба при косом изгибе составляет с осью 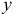 угол
угол 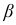 , т. е. она всегда перпендикулярна направлению нейтральной линии.
, т. е. она всегда перпендикулярна направлению нейтральной линии.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Напряженное состояние и разрушение при кручении |
| Теория прочности. Основные понятия |
| Изгиб с кручением: определение и формулы |
| Изгиб с растяжением (сжатием) |

