Оглавление:






Косой изгиб
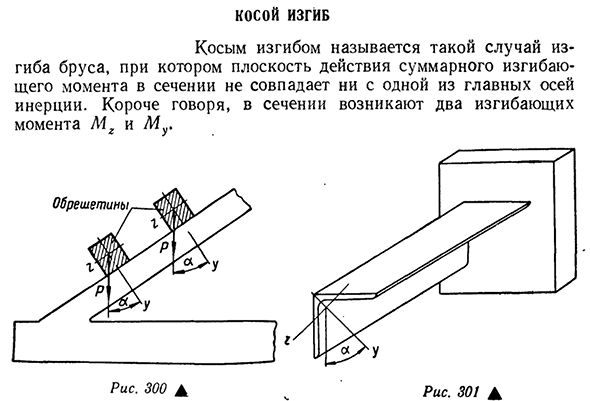
- Косой изгиб Косой изгиб-это случай изгиба балки, при котором рабочая поверхность всего изгибающего момента в сечении не совпадает ни с одной из инерционных осей. Короче говоря, есть два изгибающих момента m g и m y в разрезе. Например, крыша прогибается на 348 квадратных метров(рис. 300) работа на косом изгибе. Вес крыши и вертикальная нагрузка от собственного веса обрешетки наклоняются к главной оси на определенный угол А.
Чистый вес углов, скрепленных одним концом со стеной(рис. 301) вызывает косой изгиб, так как основная ось углового сечения наклонена к грузу под определенным углом. Рассмотрим отдельно ряд наиболее важных вопросов, связанных с расчетом стержня косого изгиба. 1. Определение давления при косом изгибе Рассмотрим балку, герметизированную на одном конце, на которую воздействует сила Р, приложенная к центру тяжести концевого участка под углом а к оси ОУ(рис. 302). Тонны 1 2 Икс п Рис 302D Раскладываем силу Р вдоль осей координат на две составляющие: Р У=Р Соса;Р РГ-R51pa.
(Слизь) Изгибающий момент сечения TP для инерциальной главной оси в соответствии с установленными правилами знака определяется Людмила Фирмаль
уравнением: Mg—RUX= — RH co8a; Mi= — R; x-RH81p a. (11.2) Поэтому в каждом сечении стержня действуют одновременно два изгибающих момента, приводящих к изгибу в двух основных плоскостях. Чтобы определить напряжение от каждого момента отдельно, используйте ранее полученную формулу для плоского изгиба. Используя принцип независимости сил, мы можем- Нет необходимости писать общую формулу напряжения в любой точке положительной четверти 349 координатных осей, Миллиграмм 2. И= (11.3) По формуле (11.3)можно определить напряжение в любой точке сечения. Вместо этого
возьмите эту официальную координату любой точки с учетом ее знаков и получите значение напряжения в этом отношении. В случае угловых точек координаты по модулю y и g получают максимальное значение, поэтому формулу (11.3) можно выразить как * Пгт== Здесь 1^g-момент сопротивления сечения. Для точек 1, 2, 3 и 4 (рис. 303), принимая во внимание физический смысл задачи при определении знака、: Г • Рух РГ х^у Рух РГ х +г , Рух РГ х в , +1gu Рух РГ х Максимальное растягивающее напряжение составит точку 2, максимальное сжатие-4. Вы можете построить график напряжения, рассчитав напряжение в четырех точках. Существует два способа построить наклонный изгиб. Первый-построить график на
- поверхности сечения, как показано на рисунке. 303, A. После удаления нулевой точки эпюры напряжений на грани сечения можно провести нейтральную линию, в противном случае напряжения всех точек будут пересекать нулевую линию NN под углом, плоскость следа AB силы равна нулю. Второй метод используется для построения пространственной диаграммы напряжений, как показано на рисунке. Так как мы рассчитали максимальное напряжение при косом изгибе 303, Б, то можно проверить прочность стержня путем сравнения полученного напряжения с рассчитанным сопротивлением. Формула(11,4) может быть использована только для точек,
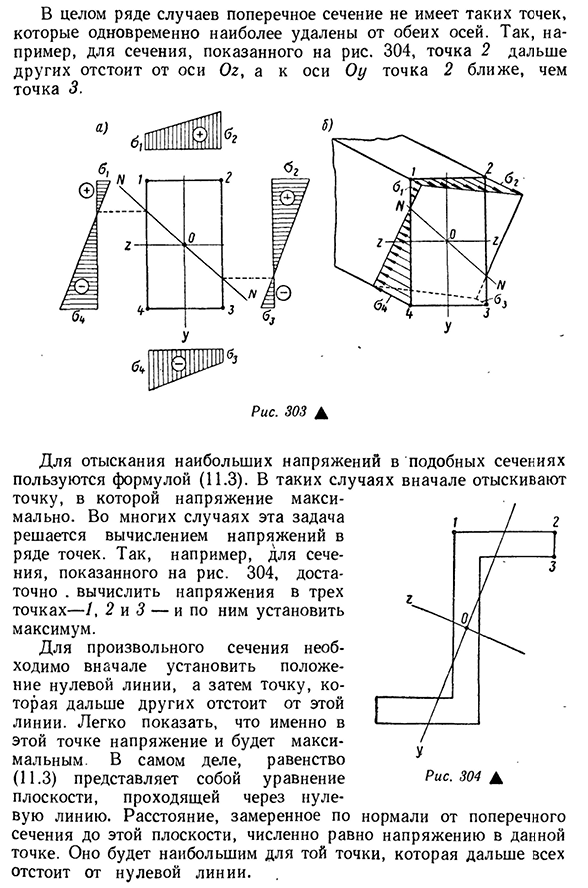
принадлежащих одновременно волокнам, наиболее удаленным от основной оси инерции section.applied.In чаще всего поперечное сечение не имеет таких точек и в то же время является наиболее удаленным от обеих осей. Например, о разделе, показанном на рисунке. Например, Точка 2 находится дальше от оси Og, чем другие точки, А Точка 2 ближе к оси OU, чем точка 3. Рис 303а Рис 304D Например, для Seche-304, Дост- Максимальные условия напряжения используются в Формуле (11.3). В таких случаях сначала находят точку, в которой напряжение максимально. Часто эта задача решается путем расчета напряжений в нескольких точках.
Поэтому NII показан на рисунке. Вот именно!. Рассчитайте напряжение в трех точках-1, 2 и 3, и установите максимальное значение. В любом сечении нужно Людмила Фирмаль
сначала установить положение нулевой линии, а затем наиболее удаленные точки от остальных. Легко показать, что в это время напряжение будет максимальным. Фактически равенство (11.3) является уравнением плоскости, проходящей через нулевую линию. Расстояние, измеренное поперечным сечением до этой плоскости, численно равно напряжению в этой точке. Это будет максимум для самых удаленных точек от нулевой линии. Из нормального от креста 3512 определение положения нулевой линии в поперечном сечении балки при косом изгибе Положение нулевой линии при косом изгибе можно установить путем выравнивания напряжения в точке,
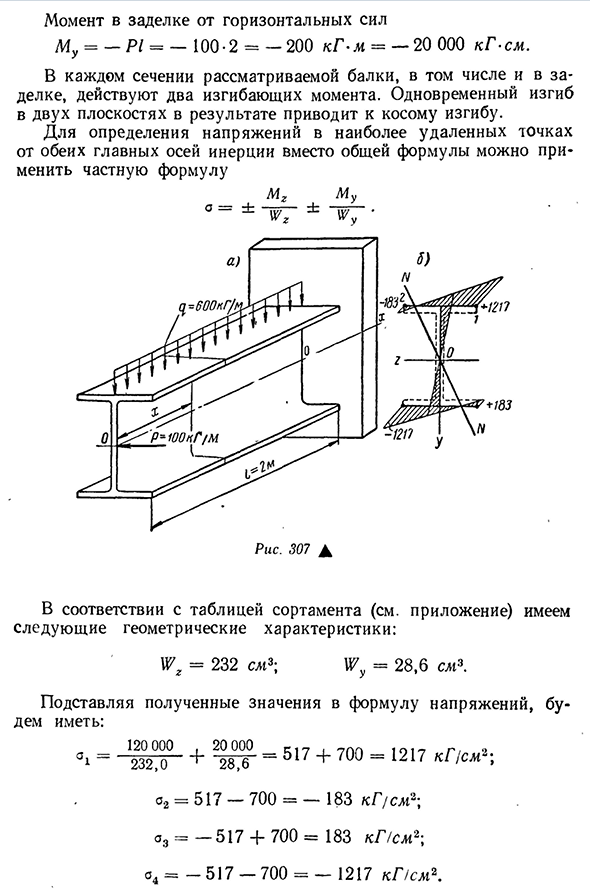
принадлежащей этой линии, до нуля. Предположим, что текущие координаты нулевой линии равны yy и g^, а затем применяем формулу (11.3) к、 Иметь N+ Где его найти Уй Му у мг (П. Пять) Правая часть уравнения (11.5) положительна, если оси выбраны так, что моменты m y и M2 имеют одинаковый знак. В этом случае знак y и y при заполнении формулы (11.5)!y и g/> / различны. Поэтому «нулевая линия» не может пройти через первую четверть(рис. 305, а). Учитывая, что через Og O2=517-700= — 183кг / см2;A3^ _ _517 4-700=183кг/см2;O4= — 517-700= — 1217кг / см2. Двенадцать. 355 согласно этим данным строится диаграмма напряжений для участка в
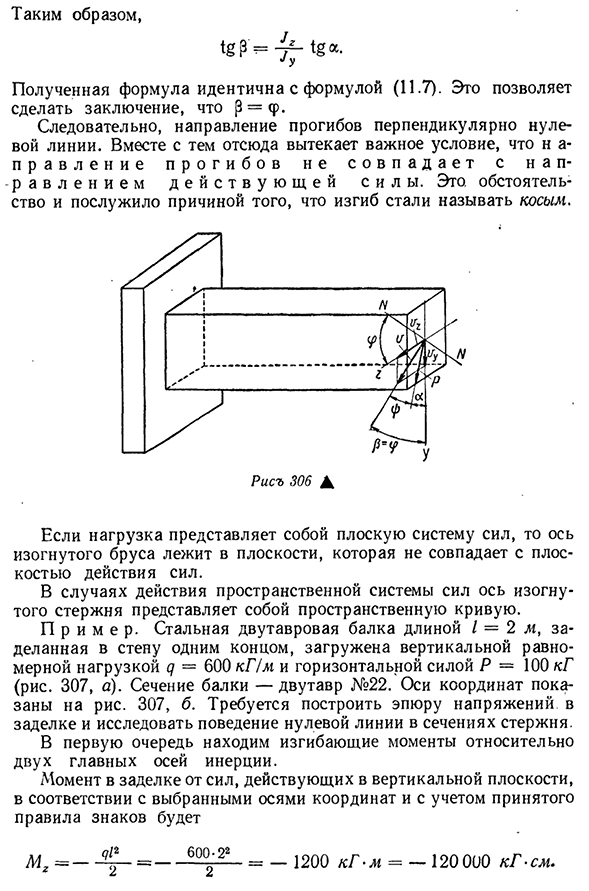
уплотнении, которая показана на рисунке. Это указывает на напряжение в самой дальней точке полки и средней линии стены. Найдите положение нулевой линии в уплотнении. Подставим значение изгибающего момента в Формулу (11.6) и учтем его=2550pch4;<1U=157SL14 (см. ассортимент), получим . 20 000 2550o f— — 120 000 * 157 — 2 ,7 ‘ Следовательно, f=69°45’. Как показано на рисунке, нулевая линия проходит через вторую и четвертую четверти, поскольку угол касания<p был положительным. 307, b. поскольку напряжение в этом отношении равно нулю,оно очень
согласуется с построенным сюжетом А. Интересно отметить, что на разных участках луча угол наклона нулевой линии разный. Для любого участка, взятого на расстоянии x от свободного конца, мы имеем. Л М U=м. = — RH2550 5.41 ‘ DH2 ‘ 157=x2 Около х-0С=90°;х = 1.0 м F=79°35′. x=2,0 м f=69°45’.
Смотрите также:
| Сложное сопротивление общие понятия | Одновременное действие изгиба и продольной силы |
| Построение эпюр внутренних усилий для стержня с ломаной осью | Внецентренное действие продольной силы |

