Оглавление:

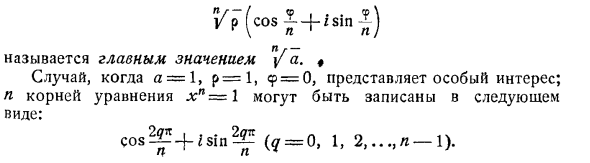

Корни из комплексных чисел
- Сложный корень. До настоящего времени никакое значение не было присвоено таким символам, как a, a и a / n. Где a — комплексное число, а m и n — целые числа. Тем не менее, кажется естественным принять определение, данное в элементарной алгебре, для фактического значения a.
- Поэтому мы решаем P g- Разделите на a или n1 / «. N является положительным целым числом как числом, которое удовлетворяет выражению zn = a, am / n является целым числом, таким как m является (a1 / l) m. Эти определения Есть корень этого уравнения?
Решение уравнения zn = a. Людмила Фирмаль
Дай мне a = p (cos 9 + i sin 9), Где p положительно, а 9 — угол -mc <^ 9 ^ mc. Если 2 = r (cos 0 -) — / sin b), уравнение принимает вид: g «(cos n 6 i sin n 6) = p (cos 9 -f-i sin 9), Вот так r «= p, cosa * 0 = cos9, sinn 6 = sin9. (1) Единственное возможное значение для r это j / p.
| Уравнения z*-{-l =0 | Функции от положительного целочисленного переменного |
| Диаграмма Аргана | Интерполяция |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Это нормальный арифметический корень порядка от p до n. N 6 = 9 26 тг (k является целым числом) или для двух последних уравнений, которые должны быть выполнены е == _? + 2fa: ^ n k == pn + qt, где p и q являются целыми числами, а 0, 0 равно 2π / 7-, а значение p не имеет значения. Следовательно, уравнение zn = a =: p (cos 9-i-sin 9) С интенсивными n корнями, заданными формулой z = r (cos 8-f-fsinG), где r = Vi, 0 = «+ = 0, 1, 2, …,» -1). Вы можете легко увидеть, что эти n корней различны, нанеся их на диаграмму Аргана. корень
V? (Cos £ -f isin £) Называется главное значение / а. * Это особенно важно, когда a = 1, p = 1 и 9 = 0. N корней уравнения xn- \ можно записать в виде потому что ^ + есть? ^ (Q = 0, 1, 2, …, n-1). Эти числа называются корнями n-го порядка единицы. главный Значение является самой единицей. При показе cos — {- н ‘ 2G -f-1
Корень порядка n из sin-unity можно записать как: «2 н к 1 1, ••• «»> / «. Людмила Фирмаль

