Линейной комбинацией векторов называется сумма произведений этих векторов на какие-либо числа, например: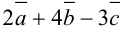 
.
Справедливы следующие теоремы:
1. Любой вектор плоскости может быть представлен единственным образом в виде линейной комбинации двух неколлинеарных векторов 
и 
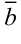, т.е.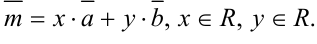 
2. Любой вектор пространства может быть представлен единственным образом в виде линейной комбинации трёх некомпланарных векторов , 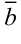и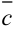 
, т.е.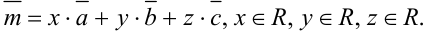 
Говорят, что вектор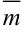 
разложен по базису.
Базисом на плоскости называется пара неколлинеарных векторов, взятых в определенном порядке. Базисом в пространстве называется три некомпланарных вектора, взятых в определенном порядке.
Введем понятие прямоугольной декартовой системы координат на плоскости и в пространстве.
Прямоугольные координаты
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Операции над векторами как над направленными отрезками. |
| Скалярное произведение векторов. |
| Операции над векторами в координатах. |
| Уравнение линии на плоскости. |
