Координаты в пространстве и система координат

Координаты в пространстве

• Пространственные координаты Ввести систему координат в пространстве, чтобы позволить геометрическую интерпретацию функции двух переменных. Возьмите три прямые, которые ортогональны друг другу и пересекаются в одной точке, каждая 1) устанавливает направление, 2) выбирает единицу измерения масштаба и 3) указывает на начало координат. Обычно масштаб считается одинаковым для всех трех линий, а контрольной точкой является пересечение этих линий.

Набор из трех пересекающихся линий, которые ортогональны друг другу в одной точке, называется 1) направление установлено, 2) введена шкала, 3) выбрано начало координат, называется системой координат

Каждая из этих линий называется координатной осью, одна — горизонтальная ось или ось Ox, другая — ордината или ось Oy, а третья — соединительная ось или ось Oz. Людмила Фирмаль

Контрольная точка, общая для трех осей, называется началом координат и обозначается буквой O. На рисунке 5 показано направление положительной оси. 99. Пусть P — любая точка в пространстве. Вертикальная линия на оси координат опущена, а проекция точки на ось Ox называется буквой A, буква на оси Oy называется B, а точка на оси Oz называется C (рисунок 99). х Сегменты OA, OB и OS называются точечными координатными сегментами P (см. Главу 1). Определение координат точки остается таким же, как секунды. Добавлю только, что координаты, измеренные вдоль оси Oz, называются приложениями.

Точка Pt с номером абсциссы x, номером ординаты y и номером перекрытия z записывается как P (x, y, z). Точки A, B и C можно получить разными способами. На это указывает точка А (рисунок 99). Проецируйте точку P на плоскость xOy. То есть, опустить вертикальную линию на этой плоскости. Получи точку М. Опустите перпендикуляр от М до оси Ох. Основы перпендикуляра Рисунок 99.

• Получить этот самолет, точка М. Опустите перпендикуляр от М до оси Ох. Основой перпендикуляра к оси Ox является точно точка A (это получается из трех перпендикулярных теорем). Во многих случаях при представлении точки P для ясности кубоид рисуется вместе с осями координат.

Три ребра находятся на координатных осях. На рисунке 99 показан параллелепипед OAMBCLPN. Тогда становится ясно, что OA = BM = x, OB = AM = y, OC = MP = z.

Одна из вершин прямоугольника находится в указанной точке P, а противоположная точка находится в начале O. Людмила Фирмаль

И этот OP — диагональ коробки. Поскольку JRO и DOLAT являются прямоугольными, OP2 = OM2 -f MP2 и OM2 = OA2 f + AM2 и OP2 = OA2 + AM2 + MP2 = x2 + y2 + z2 и OP = Vx2 + f + z2. Таким образом, расстояние от начала координат равно квадратному корню из суммы квадратов координат. Задача 1. Найти расстояние между точками Px (xx, yv zx) И P2 (xi >>> zi) -.

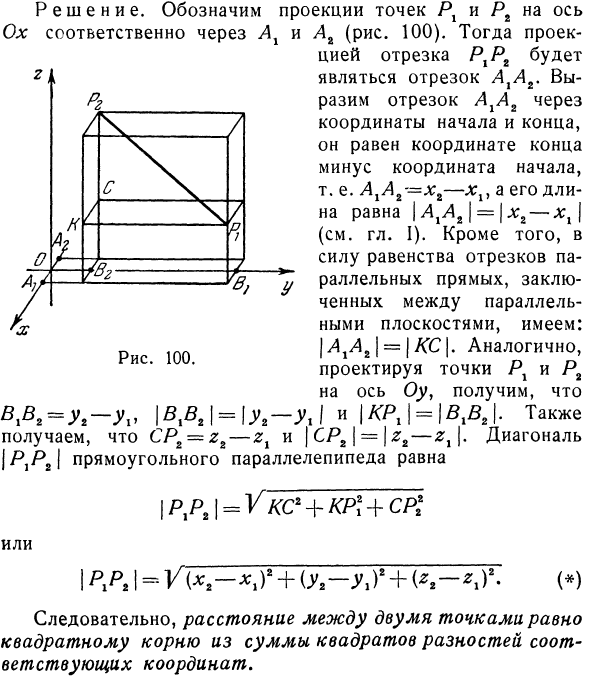
Решения. Проекции точек P1 и P2 на ось Ox показаны через A1 и L2 соответственно (рис. 100). В этом случае проекция сегмента PXP2 является сегментом AtAt. Сегмент AxAg представлен начальными и конечными координатами. Это равно конечной координате минус начальная координата, т. Е. От A1A2 до x2-x1Y, длина которой \ A1A2 \ = \ xg-xx | (см. Главу 1).

Кроме того, поскольку отрезки параллельных линий, заключенных в параллельную плоскость, равны, это \ AxA2 \ — \ KC . Аналогично, проецируя точки Px и P2 на ось Oy, получаем = \ B> B2 \ = \ y2-yy \ and \ KPx \ = \ BxBt . также Получите CP2-z2-zx и \ CP2 \ — \ z2-zx |. Прямоугольный параллелепипед \ РХР2 \ равен | pgr21 = VKS2 + KP1 + CP \ или I PA I = Vix-xj + (y r-A) ‘+ (*) Таким образом, расстояние между двумя точками равно квадратному корню из суммы квадратов соответствующих разностей координат. Рисунок 100

Смотрите также:

Предмет высшая математика

Формула Симпсона	Некоторые простые уравнения
Функции многих переменных	Поверхности