Контрольная работа по прикладной механике с решением

Готовая контрольная работа по прикладной механике.

Цель дисциплины «Прикладная механика» состоит в необходимости научить будущих инженеров-экологов правильно ориентироваться в выборе конструкционных материалов и конструктивных форм, обеспечивать высокие показатели надежности, долговечности и безопасности напряженных конструкций и узлов оборудования, владеть принципиальными основами подхода к прочностному расчету конструкций и самостоятельно отслеживать тенденции и перспективы развития науки о прочности конструкций.

Важнейшим условием создания новых конструкций машин и приборов являются качественные и всесторонние исследования в области прочности, которые должны обеспечить эффективный поиск рациональных технических решений. Основными задачами данной дисциплины являются следующие: научить студентов выбирать расчетные схемы, проводить расчеты типовых элементов конструкций, сравнивать варианты, отыскивать оптимальные решения, связывать воедино инженерную постановку задачи, расчет и проектирование, учитывая профиль будущего специалиста.

Правильное решение контрольных расчетов на прочность, жесткость и устойчивость конструкций, используемых в сложных эксплуатационных условиях под действием как статических, так и динамических нагрузок, учет температурных воздействий и процессов, связанных с длительностью эксплуатации, является необходимым условием надежности и долговечности машин и аппаратов при одновременном улучшении их весовых показателей.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Прикладная механика

Наука, изучающая движение и взаимодействие материальных тел, называется прикладной механикой . Механика рассматривает «внешние» движения моделей действительных материальных тел и их причины, отвлекаясь от «скрытых» молекулярных и атомных движений. Таким образом, в поле зрения механики не попадают тепловые и электромагнитные явления, изучаемые в физике. Если необходимо, действие электрических и магнитных явлений заменяется в механике заданным полем сил.

Курс прикладной механики естественным образом подразделяется на две основные части: механика твердого (недеформируемого) тела и механика деформируемого тела. В зависимости от специализации обучаемых и направления подготовки в различных технических ВУЗах могут различаться дисциплины, в рамках которых изучаются данные разделы механики.

Основные принципы прикладной механики

• Перемещения малы по сравнению с размерами тела. Относительные удлинения и углы сдвига считаются малыми по сравнению с размерами тела.
• Принцип независимости действия внешних сил. Этот принцип позволяет пользоваться законом сложения сил.
• Локальность эффекта самоуравновешенных нагрузок (принцип Сен-Венана). Это означает, что распределение внутренних напряжений зависит только от статического эквивалента приложенных сил, а не от способа приложения нагрузки.

Возможно эта страница вам будет полезна:

Предмет прикладная механика

Внутренние напряжения в твердом теле

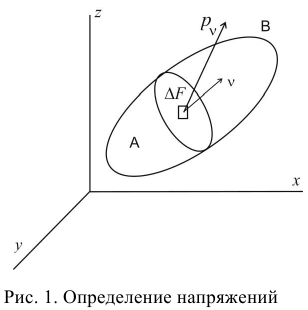
Под действием внешней нагрузки в теле возникают внутренние напряжения. Для их определения мысленно рассечем тело на две част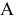и и 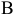(рис. 1). Плоскость сечения определяется нормалью 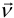, внешней по отношению к .

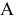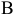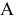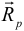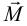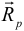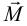Действие части на часть описывается силой , приложенной к центру тяжести сечения, и парой сил с моментом . Векторы и называются усилиями в сечении.

Они являются равнодействующими элементарных сил 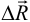, распределенных по сечению 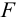по всем бесконечно малым площадям 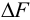, на которые можно разбить это сечение.

Определение. Интенсивность этих внутренних сил называется напряжением:

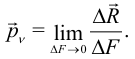
Проекции вектора 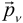на направления осей принято обозначать 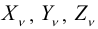. В данной точке вектор 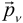зависит от выбора площадки, иными словами, от выбора направления нормали .

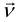Напряжения на любой площадке, проходящей через данную точку, можно выразить через напряжения на площадках, параллельных координатным плоскостям. Для таких площадок вместо индекса 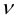будем использовать индекс оси координат, которой параллелен вектор 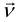. Примем обозначения для компонентов вектора интенсивности напряжений:

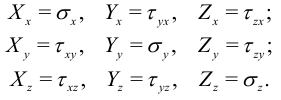
Эти величины называют напряжениями. Растягивающие напряжения принято считать положительными. Напряжения измеряются в 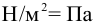(Паскали). Паскаль — очень маленькая единица измерения, поэтому на практике пользуются Мегапаскалями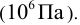

Силовые факторы в стержне

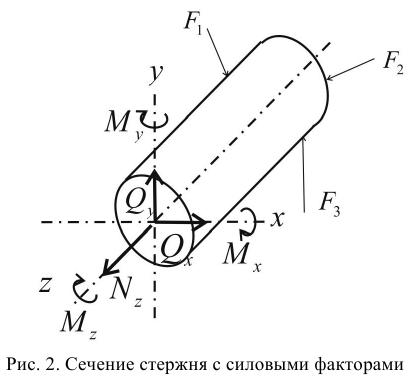
Пусть стержень под действием внешних сил находится в равновесии (см. рис.2).

Мысленно рассечем его какой-либо плоскостью и левую часть отбросим. Действие отброшенной части заменим системой сил в сечении. При помощи условий равновесия можно определить главный вектор 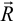и главный момент 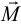внутренних сил, действующих в центре тяжести сечения. Можно сказать, что в данном сечении левая часть тела действует на правую посредством внутренней силы 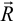и внутреннего момента 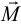, которые находятся из условий равновесия оставленной части.

Спроецируем 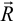и 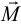на оси координат. Проекции называются:

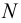— нормальная сила; 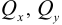— поперечные силы;

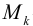— крутящий момент; 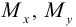— изгибающие моменты.

Основные виды нагружения стержня.

Как правило, изучаются случаи нагружения, при которых большая часть внутренних силовых факторов равна нулю. Основные виды нагружения различаются по отличным от нуля факторам:

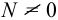— растяжение или сжатие;

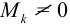— кручение;

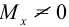(или 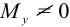)- чистый изгиб;

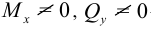— поперечный изгиб в плоскости .

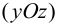Система для расчетов на компьютере.

Для проведения стандартных видов расчета научно-техническим центром АПМ создан комплекс программ АРМ WinMachine [13]. Наиболее важны в механике деформируемого твердого тела следующие модули:

АРМ Beam — расчет стержней на поперечный изгиб;

АРМ Shaft — расчет валов на изгиб и кручение;

АРМ FEM — расчет напряженного состояния методом конечных элементов (компонент программы «Компас»);

АРМ Structure3D — расчет стержневых и пластинчатых пространственных конструкций.

Тензор напряжений. Типы напряженного состояния

Уравнения равновесия твердого деформируемого тела

Напряжения, введенные выше, объединяются в матрицу, называемую тензором напряжений:

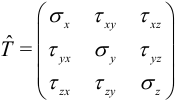
Из условий равновесия и третьего закона Ньютона следует, что эта матрица симметрична. Уравнения равновесия в декартовых координатах выполняются всегда в любо точке внутри тела и имеют следующий вид [8]:

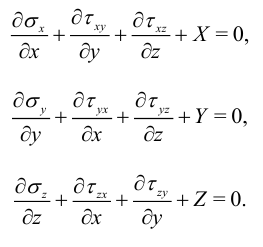
Здесь 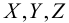— компоненты вектора плотности внешней объемной силы, которая измеряется в 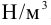. Система уравнений (2) не замкнута, поскольку содержит шесть независимых неизвестных. Кроме того, для ее замыкания нужны еще граничные условия. Внешние силы должны быть заданы.

Вектор интенсивности напряжений на произвольной площадке можно выразить через векторы напряжений на координатных площадках, то есть через компоненты тензора напряжений. Для этого рассмотрим деформированное твердое тело в состоянии равновесия под действием внешних сил.

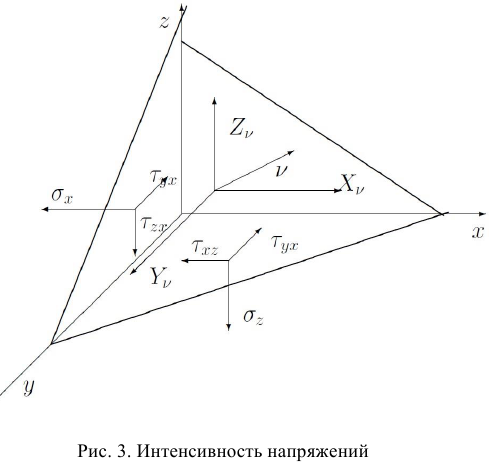
Выделим в нем малый тетраэдр (рис.3), три грани которого параллельны координатным плоскостям, а четвертая определяется вектором нормали:

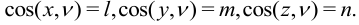
Площади граней:

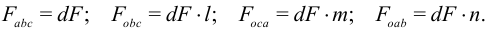
Тетраэдр находится в равновесии, и на него действуют следующие силы:

1) На координатных площадках — составляющие напряжений ,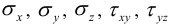

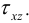
2) На площадке 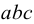— силы от составляющих вектора напряжения .

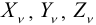3) Составляющие объемной силы .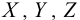

Полагая (по определению напряжения) силу равной произведению площади на напряжение, после проецирования всех сил на ось 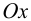получим:

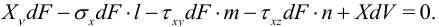
Считая тетраэдр бесконечно малым, пренебрегаем объемной компонентой, а именно, силой 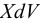. Отсюда получим выражение напряжений на произвольной площадке через напряжения на координатных площадках:

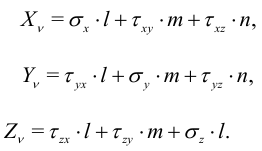
Главные площадки и напряжения

Рассмотрим частный случай 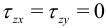. Этому соответствует случай, когда на тело (например, брус) действуют силы в плоскости 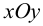, не зависящие от координаты 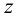. Пусть нам известны все компоненты тензора напряжений. Требуется найти площадки, на которых касательные напряжения равны нулю. Для двумерного случая решение поставленной задачи дается уравнениями:

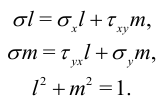
Здесь 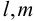— направляющие косинусы вектора нормали к искомой площадке, 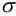— нормальное напряжение на этой площадке. Первые два уравнения представим в виде

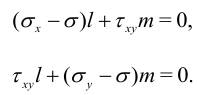
Условие разрешимости этой системы

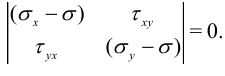
Решая это квадратное уравнение, получим два значения 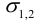, на двух взаимно перпендикулярных площадках. Принято нумеровать значения в порядке .

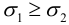Направление 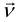найдем из одного из уравнений (3) и условия

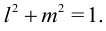
Определение. Площадки, на которых касательные напряжения равны нулю, называются главными.

Максимальное касательное напряжение в данной точке тела выражается через напряжения на главных площадках:

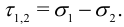
Аналогичные результаты для трехмерной задачи есть, например, в [10].

Состояние чистого сдвига.

Пусть

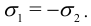
Тогда

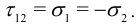
Определение. Состоянием чистого сдвига называют такое плоское напряженное состояние, при котором в окрестности любой точки можно выделить элемент так, что на его четырех гранях отличны от нуля только равные между собой касательные напряжения.

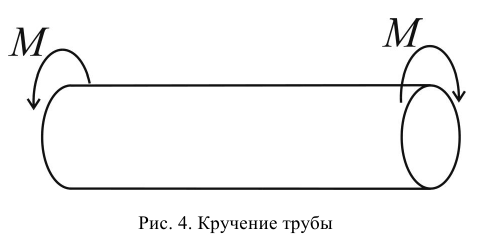
В качестве примера можно привести задачу о кручении тонкостенной трубы на рис. 4. Можно доказать, что данная нагрузка ведет к состоянию чистого сдвига.

Основы теории деформаций

Удлинение стержня и закон Гука

Пусть стержень растянут силой 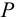. После приложения силы его длина стала 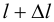, где 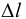называется абсолютным удлинением стержня. Возникло т.н. однородное напряженное состояние, при котором напряжения во всех точках одинаковы.

Относительным удлинением назовем величину

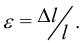
Величина 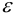называется еще осевой деформацией стержня.

Пусть при неоднородной деформации точка стержня с координатой 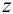сместилась на расстояние 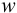, а точка с координатой 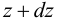сместилась на расстояние 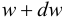. Тогда осевую деформацию участка стержня между этими точками найдем по определению

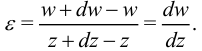
Полученное соотношение (4) является общим и демонстрирует различие между деформацией 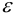в точке с координатой 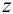и перемещением 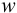этой точки.

Для состояния чистого растяжения выполняется закон Гука

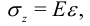
где 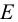— модуль Юнга. Отсюда можно вывести формулу для удлинения стержня первоначальной длины 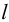. Верна цепочка равенств:

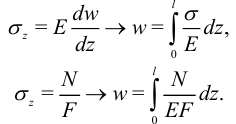
Этими формулами можно пользоваться при построении эпюры перемещений по эпюре внутренних усилий.

Перемещения и деформации в твердом теле

Пусть точка твердого тела 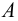с координатами 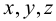при деформации перемещается в точку 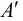с координатами 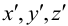. Вектор 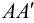назовем вектором перемещения точки :

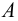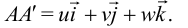
По определению, координатами вектора перемещения будут величины

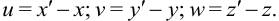
Координаты вектора перемещения являются функциями координат точки :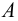

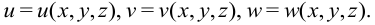
Деформирование тела вызывается разницей в перемещениях его различных точек.

Рассмотрим деформирование параллелепипеда на рис. 5.

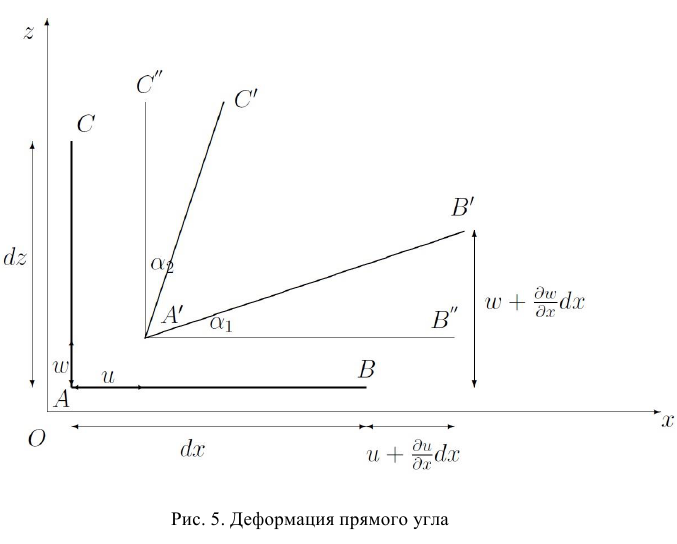
Длина проекции ребра 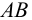на ось :

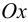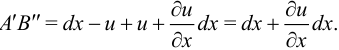
Проекция абсолютного удлинения 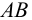на ось :

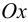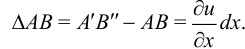
Относительное удлинение 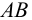вдоль оси :

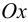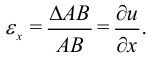
Эта величина является линейной деформацией по направлению оси 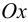. Аналогично получим:

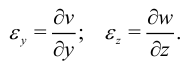
Рассмотрим изменение углов при деформации. Тангенс угла поворота отрезка 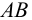в плоскости 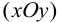равен

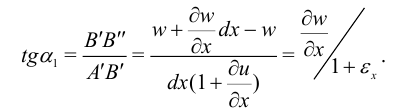
Считая деформацию малой, положим:

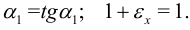
Отсюда следует, что

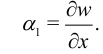
Аналогично выполнено равенство:

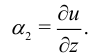
Угол сдвига в плоскости 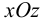(искажение прямого угла 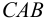) называется угловой деформацией и определяется как сумма углов поворота ребер 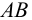и :

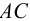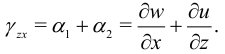
Аналогично

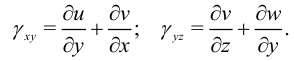
Очевидно, что

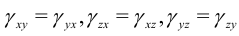
в силу определения угловых деформаций.

Выражение деформаций через перемещения называются уравнениями Коши:

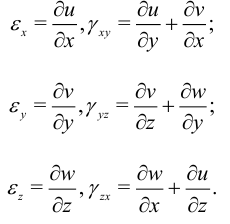
Объемная деформация.

Вычислим изменение объема бесконечно малого параллелепипеда с начальным объемом 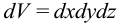. При этом пренебрежем угловыми деформациями. После деформирования длин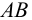а равна

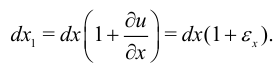
Аналогично

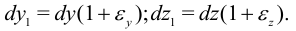
Объем полученного параллелепипеда

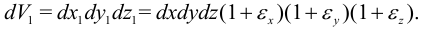
Раскроем скобки и пренебрежем произведениями деформаций как величинами второго порядка малости. Получим:

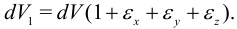
Обозначим

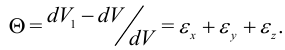
Величина 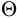называется объемной деформацией.

Закон Гука

При малых деформациях принято считать, что для чистого растяжения стержня нормальные напряжения и линейная деформация пропорциональны:

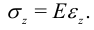
При этом имеют место поперечные деформации по закону Пуассона:

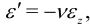
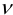— коэффициент Пуассона.

Для состояния чистого сдвига при кручении стержня экспериментально установлена зависимость

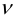
где 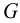— модуль сдвига, 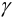— угол сдвига, 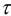— касательное напряжение. Известно,

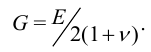
Обобщенный закон Гука.

При малых объемных деформациях выполнены соотношения

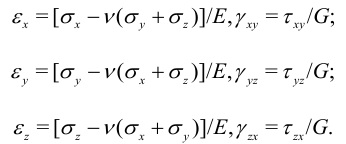
Эти соотношения называются обобщенным законом Гука [8].

Возможно эта страница вам будет полезна:

Задачи прикладной механики

Введение в механику стержня. Кручение и изгиб стержня

Сделаем несколько вводных замечаний.

Определение. Стержень — твердое деформируемое тело, один из размеров которого превышает два других.

Для стержня, как и для любого объекта, выполняются уравнения (2). Условия на поверхности получим, выписав соотношения для напряжений на произвольной площадке с нормалью :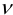

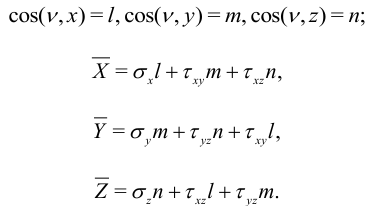
Обратим закон Гука (6), выразив напряжения через деформации

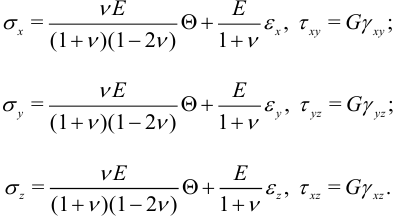
Также выполнены соотношения Коши (5). 4.1. Простейшие задачи механики стержня Рассмотрим простые задачи, которые можно найти в [8], §99. а) Растяжение в осевом направлении.

Здесь объемные силы обращаются в ноль по постановке задачи. Пусть на концы стержня действуют растягивающие силы 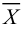. Уравнения (2) удовлетворены, если

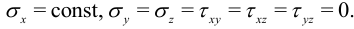
На концах стержня выполняется соотношение

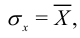
то есть внешние силы равномерно распределены по концевым сечениям стержня, б) Кручение круглого вала.

На концах круглого стержня действуют противоположно направленные крутящие моменты 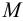. Для кручения закон Гука имеет вид

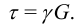
Для деформаций можно получить формулу

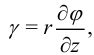
где 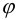— угол сдвига сечения, 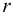— расстояние от рассматриваемой точки до центра сечения. Обозначим 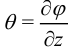— относительный угол закручивания. Тогда для напряжения получим

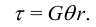
Разложим 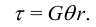на компоненты

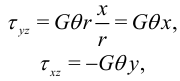
где 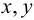— декартовы координаты в плоскости поперечного сечения. В элементарной теории принято

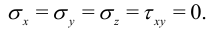
Поскольку компоненты тензора напряжений в данной задаче являются линейными функциями координат, то уравнения равновесия (2) выполнены и осталось проверить условия на поверхности. Боковая поверхность вала свободна от усилий и на ней 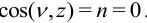. Отсюда и из (7) получим

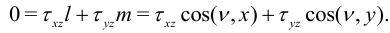
Для круглого цилиндра

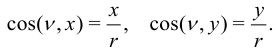
Подставим в (*) значения 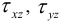и получим

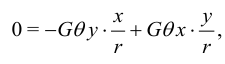
это тождество.

Таким образом, предположения элементарной теории оправданы, если поверхностные касательные усилия на торцах стержня распределены так же, как напряжения 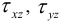в промежуточных сечениях вала.

Принцип Сен-Всиана (1855 г.). Распределение напряжений в стержне и пластине зависит только от величины и направления внешней нагрузки, но не от способа ее приложения.

Значит, на большом расстоянии от концов стержня распределение внутренних напряжений зависит только от величины крутящего момента.

в) Чистый изгиб стержня.

Пусть стержень изгибается двумя изгибающими моментами 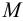, приложенными на его концах, в плоскости 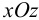. Элементарная теория дает

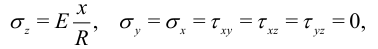
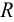— радиус кривизны стержня после изгиба. Граничные условия на боковых поверхностях удовлетворены тождественно. На концах поверхностные силы распределены как .

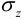Найдем отсюда изгибающий момент. По определению он равен

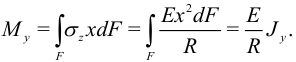
Здесь 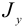— момент инерции поперечного сечения. Методом сечений можно найти 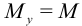. Для радиуса кривизны получим

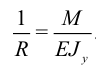
Перемещения можно найти из соотношений Коши (5). При этом предположим, что точка 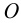закреплена и

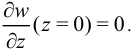
Тогда при

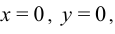
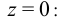
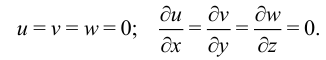
Закон Гука дает:

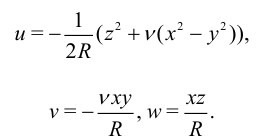
На оси стержня 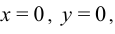получим

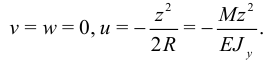
Последняя формула выражает перемещения вдоль оси 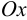, а следовательно, прогибы стержня при чистом изгибе.

Теорема Журавского-Шведлера

Выделим двумя поперечными сечениями элемент стержня длиной 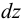, находящийся под внешней распределенной нагрузкой 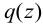(рис. 6).

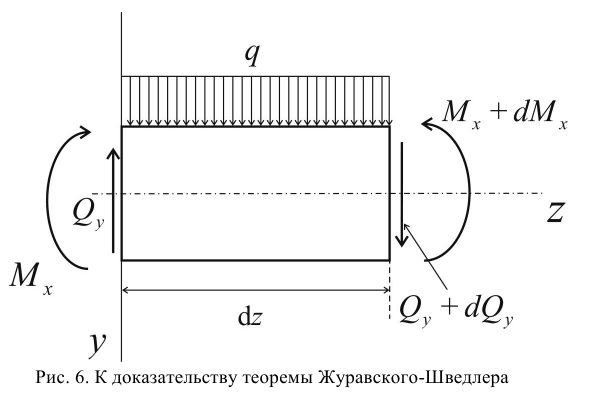
На рис. 6 на элемент 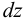действуют внутренние силовые факторы:

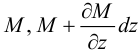— изгибающие моменты от отсеченных левой и правой частей;

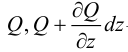— поперечные усилия.

Составим уравнения равновесия элемента :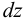

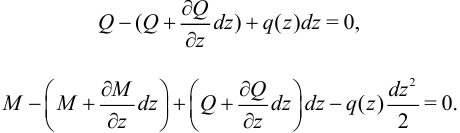
Из этих уравнений, отбрасывая вторые порядки малости, найдем:

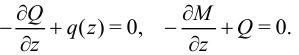
Следующие формулы выражают математически теорему Журавского-Шведлера:

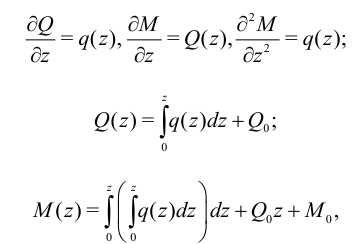
где 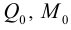— значения поперечной силы и изгибающего момента при .

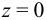Построение эпюры изгибающих моментов

Определение. Стержни, работающие на прямой изгиб, называются балками. Типы балок, изучаемые в нашем курсе: консоль, двухопорная балка, двухопорная балка с консолью.

При поперечном изгибе в стержне возникают как нормальные, так и касательные напряжения. Зависимость между внутренними силовыми факторами и напряжениями выражается формулами:

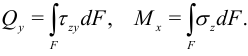
Графики функций

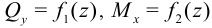
называются эпюрами поперечных сил

и изгибающих моментов. Для их построения обычно испольуют метод сечений [3]. Этот метод рекомендуется изучить по книгам [3] или [12].

На практике при построении эпюр лучше всего пользоваться пакетами прикладных программ, такими, как АРМ WinMachine (см. [13]).

В случае необходимости для построения этих графиков при отсутствии сосредоточенных изгибающих моментов в середине балки можно воспольоваться непосредственно теоремой Журавского-Шведлера.

Изгиб стержня. Уравнение изогнутой линии при прямом изгибе

Обобщение теоремы Журавского-Шведлера

Пусть в точке с координатой 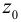на рис. 6 действует сосредоточенная сила .

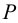Определим 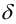-функцию Дирака следующим образом:

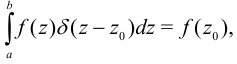
если 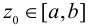. Эта функция позволяет рассматривать сосредоточенную силу 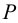как распределенную на очень малом отрезке с плотностью 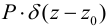. При этом необходимо потребовать выполнение условного равенства

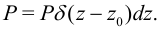
Уравнения равновесия сегмента стержня длиной 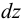принимают вид:

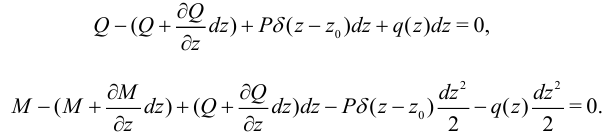
Отбрасывая величины второго порядка малости, получим

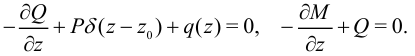
Проинтегрируем эти равенства:

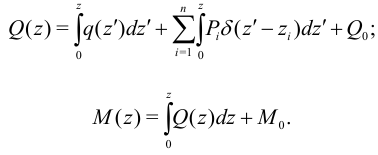
Здесь принято, что на стержень действует 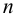сосредоточенных сил 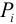в точках с координатами 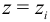. Равенства (10) выражают обобщенную теорему Журавского-Шведлера. Интеграл от 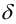-функций определяется здесь по формулам

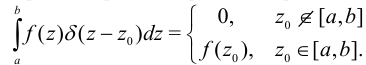
Следуя этой теореме, можно численными методами строить эпюры на компьютере, если на балку не действуют сосредоточенные изгибающие моменты.

Уравнение изогнутой линии стержня

Обозначим: 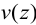— поперечное перемещение стержня в точке с координатой 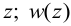— продольное перемещение.

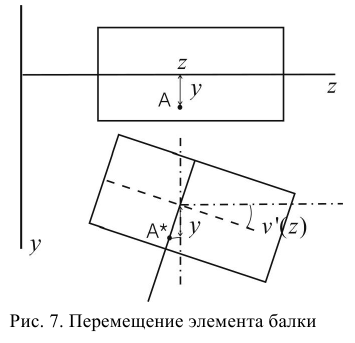
Пусть при поперечном изгибе балки точка с координатами 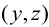переместилась, как показано на рис. 7.

Примем гипотезу плоских сечений, т.е. после деформации поперечные сечения стержня остаются плоскими. Из нее следует, что

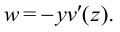
Продольная деформация по определению равна

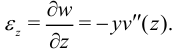
По закону Гука нормальные напряжения равны

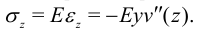
Отсюда видно, что нормальные напряжения меняются линейно по высоте сечения, и при 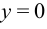(на оси стержня) .

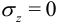Найдем изгибающий момент 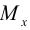. По определению, он равен

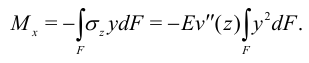
Из курса математического анализа известно, что величина 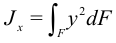называется моментом инерции сечения относительно оси .

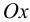Выражение для изгибающего момента относительно оси 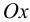через прогиб :

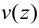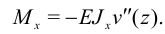
Выразим отсюда 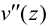и подставим результат в формулу для напряжений:

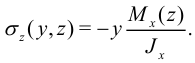
Из дифференциальных соотношений Журавского-Шведлера

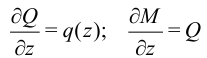
исключим с помощью формулы (11) величины :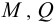

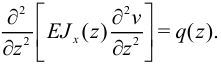
Полученное соотношение является уравнением изгиба стержня. Зная его решение 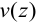, можно по формуле (11) найти изгибающий момент 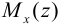и построить эпюру изгибающих моментов.

Интегралы уравнения и их физический смысл.

Последовательно интегрируя (12), получим ряд физических величин. Первый интеграл:

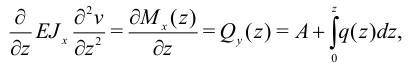
где 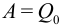— поперечное усилие при 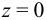. Второй интеграл:

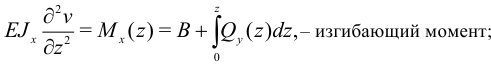
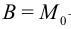— изгибающий момент при 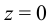. Третий интеграл:

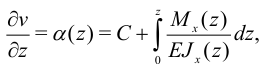
где 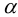— угол поворота сечения стержня, 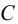— этот угол при 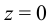. Четвертый интеграл:

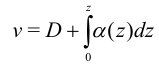
где 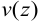— прогиб стержня, 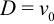— прогиб при .

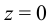Граничные условия на концах стержня и их физический смысл

В интегралы уравнения (12) входят четыре константы, значит, для постановки задачи надо добавить к этому уравнению четыре краевых условия. На каждом конце стержня обычно накладывают по два условия. Рассмотрим стандартные условия при различных способах закрепления стержня.

а) Жесткая шарнирная опора. При :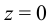

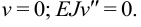
б) Жесткая заделка. Прогиб и угол поворота при 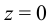равны нулю:

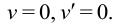
в) Свободный конец балки. Момент и поперечная сила равны нулю:

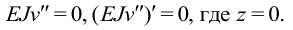
Пример:

Определить прогибы шарнирно опертой балки, загруженной на концах моментами 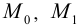и вдоль всей длины постоянной распределенной нагрузкой 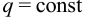. Заданы постоянные 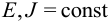. Решение.

Сформулируем краевые условия:

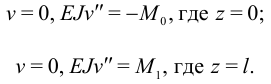
Интегрируя четыре раза уравнение (12), получим:

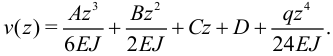
Подставляя эту формулу в краевые условия:

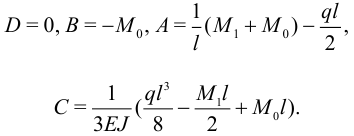
Отсюда изгибающий момент равен:

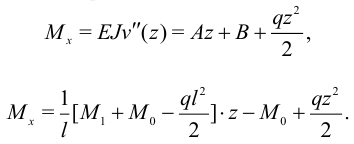
Максимальный момент найдем из условия максимума 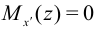. После вычислений получим максимум в точке

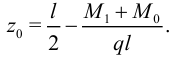
Как известно из курса математического анализа, момент принимает максимальное значение либо в точке 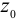, либо на концах интервала, то есть пр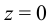и или .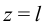

Расчет на прочность при прямом изгибе стержня. Кручение стержней

Расчет на прочность

Цель расчета: подобрать размеры сечения заданной формы так, чтобы выполнялось условие прочности. Для расчета должны быть заданы:

• а) Внешние нагрузки.
• б) Предельно допустимое напряжение .
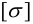• в) Форма поперечного сечения.
• г) Условия закрепления концов балки.
• д) Коэффициент запаса прочности.

При расчете обычно ставятся задачи: 1) подбор геометрических размеров сечения; 2) проверка условия прочности.

Методика расчета.

Исходная формула:

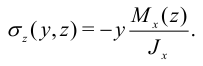
Должно выполняться условие:

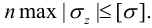
При заданном 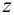напряжение максимально в наиболее удаленной от оси стержня точке при 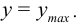. Величина 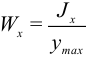называется моментом сопротивления и для стандартных сечений есть в справочниках, например, в [6]. Для прямоугольного стержня

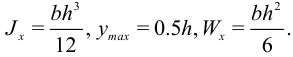
Для круглого стержня:

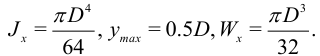
Для расчета надо найти 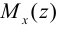, затем максимум модуля этой функции. Алгоритм расчета балки на прочность:

1) Строим эпюру изгибающих моментов. Пакет АРМ WinMachine позволяет это автоматизировать.

2) Находим момент сопротивления как функцию размеров сечения.

3) Используем формулу:

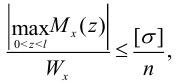
где 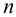— коэффициент запаса прочности, для окончательного решения задачи. Много примеров расчета приведено в книгах [2], [3], [4], [12].

Кручение круглых стержней

Определение. Кручение — такой вид деформации стержня, при котором в его поперечных сечениях возникает только крутящий момент.

Пусть один конец бруса заделан, а ко второму приложен внешний крутящий момент 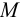. Тогда в любом поперечном сечении будет действовать крутящий момент 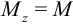. Найдем касательные напряжения, перпендикулярные радиусу круга поперечного сечения.

Элементарная касательная сила, приходящаяся на площадку 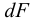, при напряжении 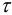равна 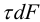, а ее момент относительно центра сечения

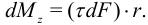
Суммируя элементарные моменты, получим:

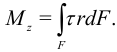
В [11] есть формула для угловой деформации:

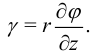
Закон Гука для сдвига 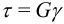, откуда:

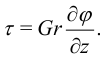
Подставляя эту формулу в (*), получим:

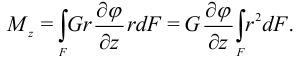
Величина

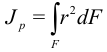
называется полярным моментом сопротивления.

Отсюда найдем формулу для углов закручивания:

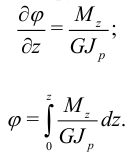
Касательное напряжение:

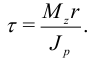
Максимальные касательные напряжения возникают на поверхности вала при :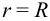

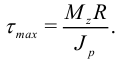
Величина 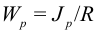. называется полярным моментом сопротивления. Формулу

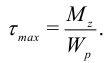
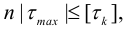
применяют и к стержням некруглого сечения. В этом случае рекомендуется брать больший коэффициент запаса прочности. Условие прочности вала при кручени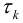и:

и 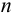должны быть заданы. В другом виде это условие:

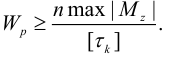
Энергия деформации при изгибе и кручении стержня

В случаях сложного деформирования напряжения в твердом теле вычисляют, исходя из вариационных принципов. Для применения этих принципов надо уметь находить изменение энергии тела при деформации. Мы кратко ознакомимся с методами вычисления этой энергии в случаях простой деформации стержня.

Энергия деформируемого тела.

Обозначим:

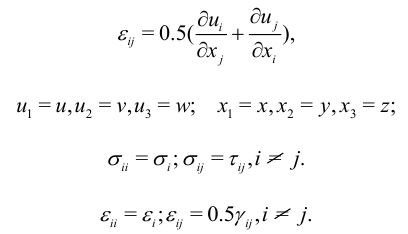
При этих обозначениях компоненты тензора деформаций:

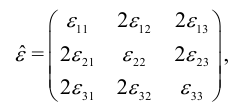
тензора напряжении

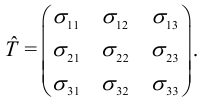
Первое начало термодинамики (см. [5]) имеет вид:

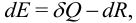
где 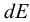— изменение внутренней энергии, 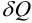— полученное телом количество теплоты, 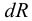— совершенная телом работа. В механике важна не 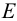, а свободная энергия 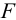[5]:

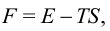
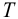— температура, 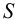— энтропия. При постоянной температуре

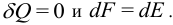
При деформировании тела совершается работа [9]:

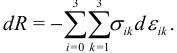
Тогда из первого начала термодинамики

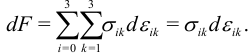
Здесь принято обычное правило суммирования по повторяющимся индексам. Можно показать, что свободная энергия деформированного тела в единице объема равна

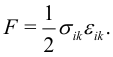
Эта же формула в старых обозначениях [9]:

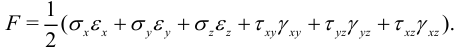
Энергия стержня при кручении.

При кручении выполняются соотношения:

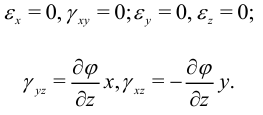
По закону Гука

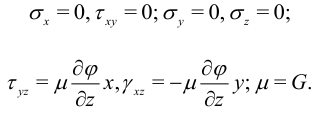
Подставляя эти значения в (15′), получим для свободной энергии бесконечно малого объема :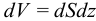

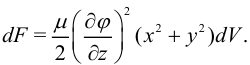
Энергия кручения отрезка 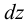стержня получается интегрированием этой формулы по площади поперечного сечения :

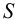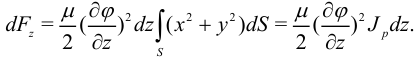
С другой стороны, угол поворота связан с крутящим моментом формулой:

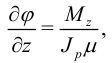
откуда следует

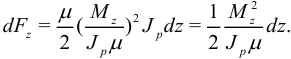
Заменяя обратно 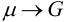, получим энергию единицы длины стержня при кручении:

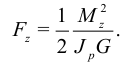
Полную свободную энергию стержня длины 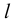при кручении получим интегрированием:

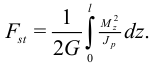
Энергия стержня при изгибе.

При чистом изгибе стержня выполнены соотношения:

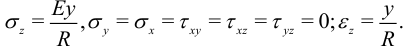
Отсюда свободная энергия единицы объема:

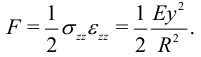
Ранее для кривизны изогнутого стержня найдено:

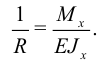
Интегрируя 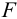по площади поперечного сечения, найдем энергию единицы длины стержня:

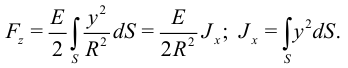
Подставим выражение для кривизны:

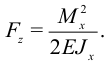
Полную энергию изогнутого стержня найдем интегрированием:

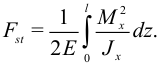
Выразим моменты и энергию через прогибы стержня :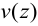

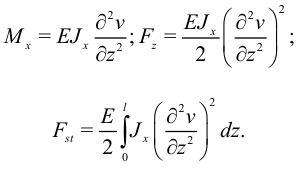
Принцип виртуальной работы

Формулировка принципа виртуальной работы. Если тело находится в состоянии равновесия, то полная работа всех сил, действующих на него, на любом виртуальном перемещении равна нулю.

Определение. Виртуальное перемещение — любое малое перемещение, совместимое с условиями сплошности материала и условиями закрепления.

Виртуальные перемещения еще называются вариациями перемещений и обозначаются 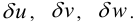Математически принцип виртуальной работы записывается так:

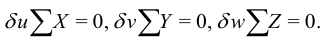
Здесь 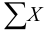— сумма проекций на ось 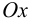всех сил, внешних и внутренних.

Работа внутренних сил равна изменению свободной энергии, взятому с обратным знаком:

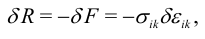
где 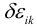— вариации деформаций. Знак минус потому, что работа совершается против сил взаимодействия между частицами. Работа внешних сил. Внешние силы делятся на:

а) Поверхностные силы 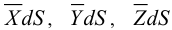, действующие на элемент поверхности .

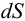б) Объемные силы 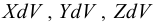, действующие на элемент объема 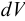. В состоянии равновесия полная виртуальная работа равна нулю:

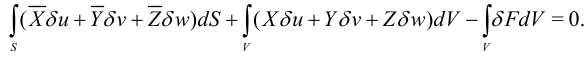
Поскольку внешние силы заданы явно, то операцию варьирования можно вынести за интеграл. Считая объемные силы равными нулю, получим:

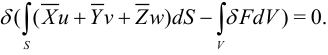
Приложение принципа виртуальной работы к выводу уравнений равновесия стержня

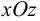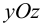Пусть стержень изгибается в двух плоскостях и распределенной поперечной нагрузкой 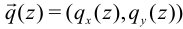. Для свободной энергии изгиба плоскости 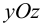ранее получена формула:

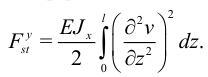
Далее считаем, что при любом 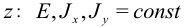. Очевидно, что для энергии изгиба в плоскости 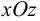выполняется аналогичная формула. Тогда полная свободная энергия стержня:

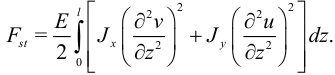
Выпишем принцип виртуальной работы для стержня:

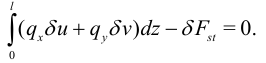
Далее пользуемся свойствами операции варьирования:

а) Для операции варьирования выполняются те же формулы, что и для дифференцирования, например:

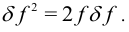
б) Операции варьирования и дифференцирования перестановочны:

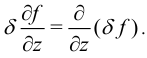
Найдем вариацию свободной энергии:

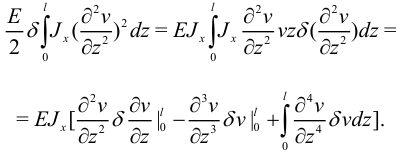
Эта формула получена путем перестановки во втором интеграле операций варьирования и дифференцирования и интегрирования по частям. Подставляя полностью проварьированную таким образом свободную энергию в принцип виртуальной работы, получим:

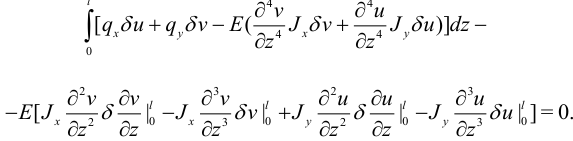
Поскольку вариации произвольны, то должны обращаться в нуль производные при них. Приведем подобные, выделив вариации величин:

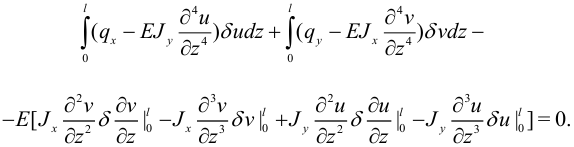
Отсюда можно сразу выписать уравнения равновесия и краевые условия для шарнирно опертой балки:

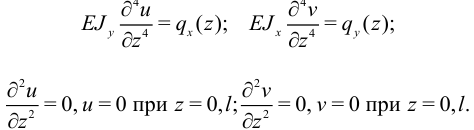
Можно также найти все интегралы, выведенные для случая плоского изгиба стержня.

Если теперь решить задачу численно на компьютере, вычислить интегралы и найти максимальный изгибающий момент, то найдем условия прочности стержня при сложной нагрузке, избегнув полуэмпирических методов сопротивления материалов.

Устойчивость стержней

Пусть стержень сжимается силой 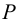, действующей вдоль его оси. При увеличении силы появляется второе, отличное от прямолинейного, положение равновесия, энергетически более выгодное. Тогда говорят, что стержень теряет устойчивость. Как правило, новое положение равновесия не описывается уравнениями, полученными ранее, потому что перемещения не малы.

Определение. Наибольшее значение сжимающей силы, при которой прямолинейная форма равновесия стержня устойчива, называется критической силой.

С точки зрения практики, критическая сила должена рассматриваться как разрушающая нагрузка.

Цель расчета на устойчивость: обеспечить работу элемента конструкции при первоначальной форме упругого равновесия, то есть при малых деформациях.

Условие расчета:

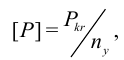
где 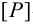— допустимая нагрузка, 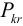— критическая сила, 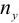— коэффициент запаса устойчивости.

Вывод формулы для критической силы

Пусть стержень потерял устойчивость и изогнулся, и пусть продолжает выполняться закон Гука, рис. 8. Тогда:

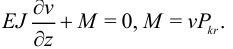
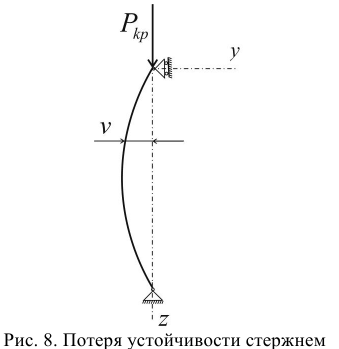
Обозначим

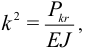
тогда

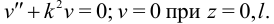
Решение этого уравнения известно:

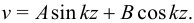
Из 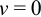при 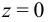следует, что 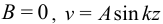. Подставляя значение 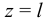, пользуемся краевым условием 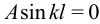. Одно из решений этого уравнения

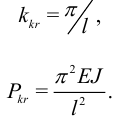
Формула (18) называется формулой Эйлера для основного случая продольного изгиба.

При других способах закрепления стержня, отличающихся от изображенного на рис.8, выполнена формула:

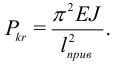
Здесь 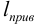— приведенная длина стержня. Часто пользуются обозначением 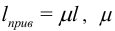— коэффициент приведения длины. Значения этого коэффициента для стандартных способов закрепления есть в [6].

Пределы применимости формулы Эйлера

Критическое напряжение, по определению, равно

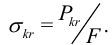
Формула Эйлера применима, если выполнен закон Гука, то есть

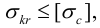
где 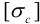— предельно допустимое напряжение на сжатие. По Эйлеру:

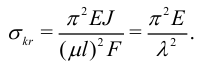
Здесь обозначено

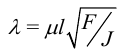
гибкость стержня.

Отсюда условие применимости формулы Эйлера запишется в виде:

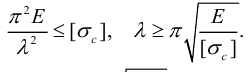
Определение. Величина

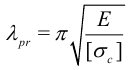
называется предельной гибкостью стержня.

Эта величина приведена в справочниках. Если гибкость меньше предельной, то вместо расчета на устойчивость нужен расчет на прочность. Предельная гибкость — это физический параметр материала.

Пример. Проверить на устойчивость сжатую стойку трубчатого сечения из хромомолибденовой стали

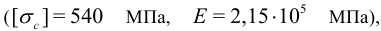
если требуемый коэффициент запаса устойчивости 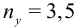. Сжимающая сила 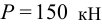, длина стойки 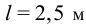, внутренний и внешний диаметры 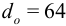, , 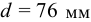коэффициент приведения длины 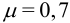. Решение.

Предельная гибкость

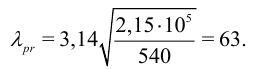
Момент инерции сечения:

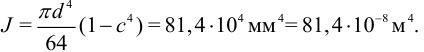
Площадь сечения

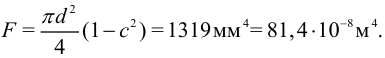
Гибкость

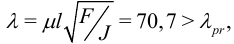
следовательно, применима формула Эйлера. В единицах СИ получим:

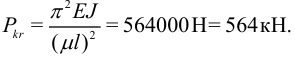
Коэффициент запаса устойчивости

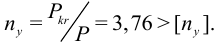
Таким образом, заданные условия устойчивости стойки выполнены.

Расчет вала с прямым изгибом

Теории прочности

При совместном действии изгиба и кручения в вале возникает сложное напряженное состояние. В этом случае нельзя ограничиться нахождением только 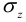для расчета на прочность, надо учесть влияние и других компонент тензора напряжений. Если привести этот тензор к диагональному виду, то, согласно диаграмме Мора, получим

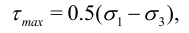
где 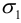— максимальное главное значение напряжения, 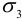— минимальное, 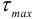— максимальное касательное напряжение. Так как наибольшее ограничение на прочность накладывается именно максимальным касательным напряжением, за критерий прочности часто принимают величину

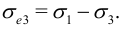
Когда в основу кладется эта величина, говорят о третьей теории прочности.

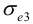называется эквивалентным напряжением и при расчете пользуются следующим условием прочности:

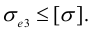
При четвертой теории прочности под эквивалентным напряжением понимают такое напряжение растяжения, при котором потенциальная энергия деформации равна энергии деформации образца. Это означает, что для эквивалентного напряжения принимают формулу:

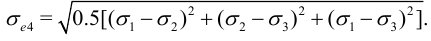
Упрощенное плоское напряженное состояние.

Выразим экстремальные главные напряжения в предположении, что напряженное состояние является плоским и от нуля отличны только 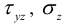. При этом

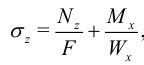
где 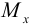— изгибающий момент, 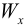— момент сопротивления.

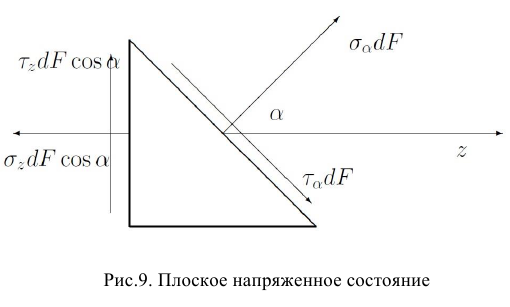
Рассматривая площадку, нормаль к которой наклонена к оси 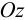, совпадающей с продольной осью стержня, под углом 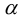(рис. 9), для нормального и касательного напряжения на ней из условий равновесия призмы получим:

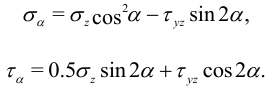
Из условия экстремальности напряжения

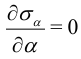
найдем

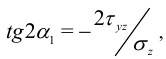
с другой стороны, условие равенства нулю касательных напряжений 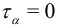дает:

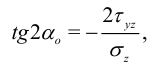
то есть экстремальные нормальные напряжения возникают на тех площадках, на которых касательные равны нулю.

Подставляя 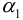в формулу для 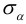, получим:

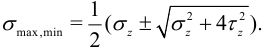
При этом 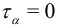, то есть эти напряжения главные, и :

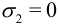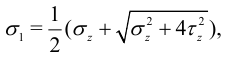
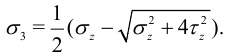
Отсюда максимальное касательное напряжение

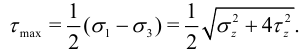
По гипотезам прочности:

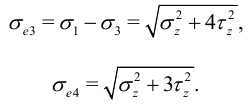
При практическом расчете валов рекомендуется пользоваться третьей теорией прочности.

10.2. Расчет вала на изгиб с кручением

При одновременном действии изгибающих и крутящих моментов учитывают два фактора: касательные напряжения от кручения 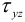и нормальные напряжения от изгиба .

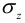Пусть на вал длины 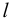насажено зубчатое колесо диаметром 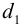и шкив ременной передачи диаметром .

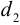На колесо действуют радиальное и окружное усилия 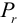и 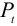, на шкив -натяжения ремня .

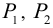Крутящие моменты выразим через действующие силы:

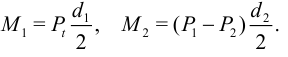
Условие равномерности вращения:

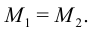
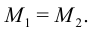должны быть заданы при постановке задачи. Силу 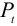определим из (*).

Затем надо обычным образом построить эпюры 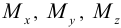. Результирующий изгибающий момент равен

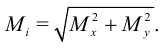
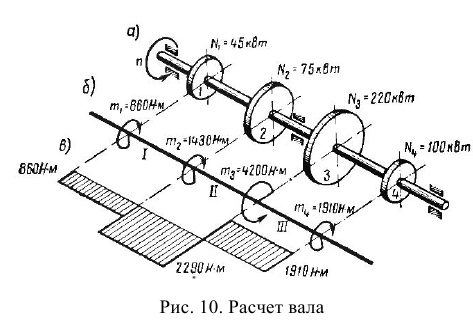
В опасной точке

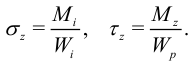
Здесь приняты обычные обозначения: 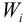— момент сопротивления сечения при изгибе, 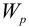— полярный момент сопротивления. Эквивалентное напряжение

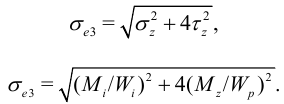
Как известно, для вала круглого (или кольцевого) сечения :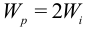

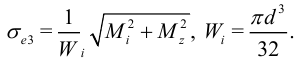
Условие прочности 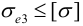, откуда следует

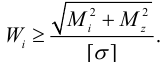
Для круглого вала получим:

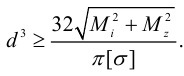
Деформации и напряжения в тонкой пластине

Основные понятия и гипотезы

Определение 1. Пластиной называется призматическое или цилиндрическое тело, высота которого мала по сравнению с размерами в плане.

Определение 2. Плоскость, делящая пластинку пополам по толщине, называется срединной. Линия пересечения боковой поверхности со срединной плоскостью называется контуром пластинки.

Координаты:

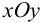— декартовы координаты в срединной плоскости, 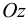— ось, направленная вертикально вниз. 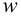— прогиб пластинки (перемещение вдоль ).

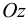Пластинка считается тонкой, если:

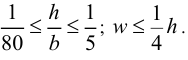
Допустимо считать тонкой пластинку, в которой выполнено

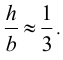
Если 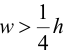, то применяют теорию гибких пластин. Гипотезы теории пластин.

Гипотеза прямых нормалей. Сдвиги в плоскостях 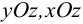отсутствуют: 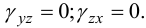Нет деформации вдоль .

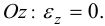Гипотеза о недеформируемости срединной плоскости: 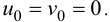. Гипотеза об отсутствии давления между слоями пластинки, параллельными срединной плоскости: .

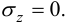Перемещения и деформации в пластинке

Как правило, из уравнений равновесия находят прогиб пластинки w. Выразим деформации через этот прогиб. Для получения этих выражений нам понадобятся формулы Коши, выражающие деформации через перемещения:

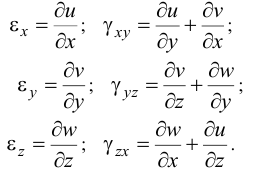
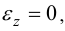следовательно, 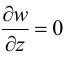— из уравнений Коши.

Это означает, что 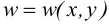— прогиб не зависит от координаты 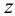. Из 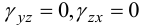следует

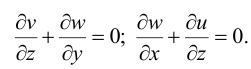
Поскольку 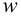не зависит от 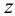, проинтегрируем эти уравнения по :

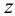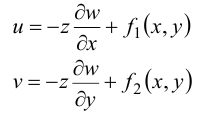
Из того, что при 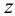= 0 (на срединной поверхности)

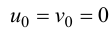
следует

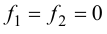
Отсюда получим

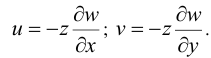
Ненулевые деформации из формул Коши равны:

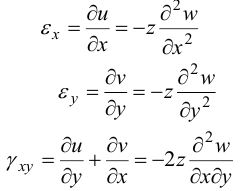
В этих уравнениях деформации выражены через прогибы .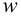

Напряжения в пластине

По предположению,

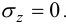
Закон Гука для нормальных напряжений

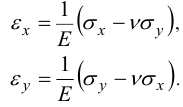
Решая систему относительно 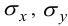, и учитывая (20):

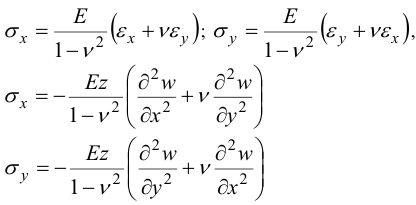
Закон Гука для сдвиговых напряжений

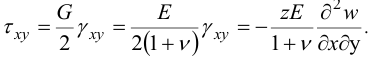
Оказывается, пользоваться законом Гука при определении 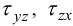нельзя, поскольку тогда получим 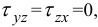согласно гипотезе прямых нормалей.

Воспользуемся непосредственно уравнениями равновесия из теории упругости, пренебрегая объемными силами:

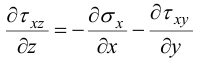
Используя (21), получим:

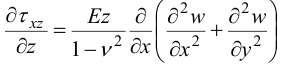
Интегрируя по :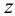

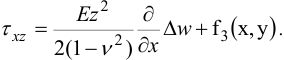
Здесь — оператор Лапласа.

Считая, что на верхней и нижней плоскостях нет касательных нагрузок, т.е.

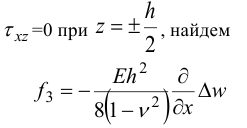
Подставляя 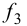в формулу для 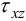, получим

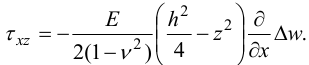
Тем же путем получим

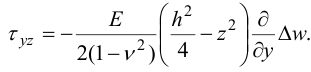
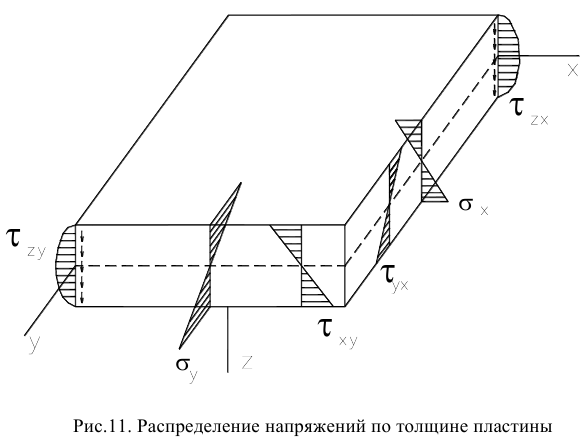
Таким образом, напряжения выражены через прогибы формулами (21), (22). На рис. 11 приведены эпюры напряжений в зависимости от вертикальной координаты в соответствии с выведенными формулами.

Усилия в тонкой пластинке

Найдем внутренние силовые факторы в сечении, перпендикулярном оси :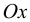

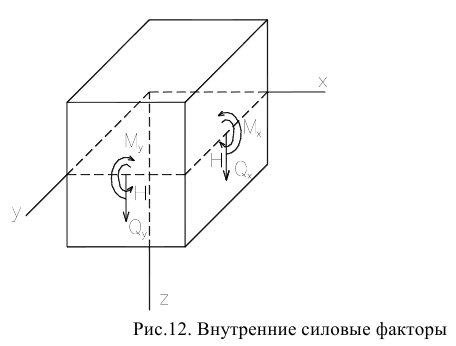
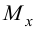— изгибающий момент
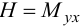— крутящий момент
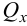— поперечная сила.

Все силы рассматриваются на единицу ширины пластины (т.е. делим на размер вдоль ).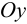

По определению

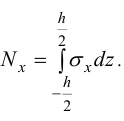
Из (21) получим:

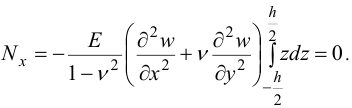
Изгибающий момент по определению:

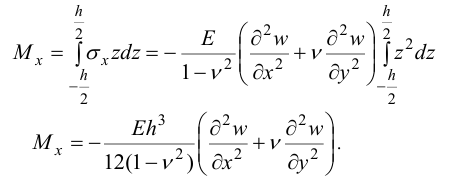
Обозначим

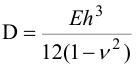
цилиндрическая жесткость пластины.

Единицы измерения изгибающего момента

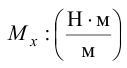
на единицу ширины.

Поперечная сила:

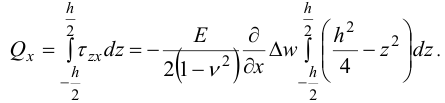
Проинтегрировав, получим:

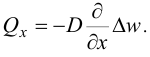
Единицы измерения: 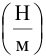на единицу ширины.

Крутящий момент:

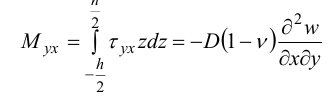
Единицы измерения: 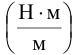на единицу ширины.

Аналогично найдем

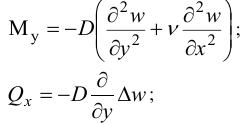
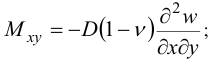
Заметим, что

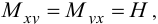
как и должно быть по третьему закону Ньютона.

Формулы (23), (24) связывают усилия в пластинке с прогибами срединной плоскости. Вычислив прогибы, можно полностью найти напряженное состояние в пластине.

Уравнение равновесия тонкой пластины

Вывод уравнения равновесия пластины

Рассмотрим равновесие элемента пластинки 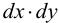. Все усилия надо умножать на длину грани, чтобы получить силу.

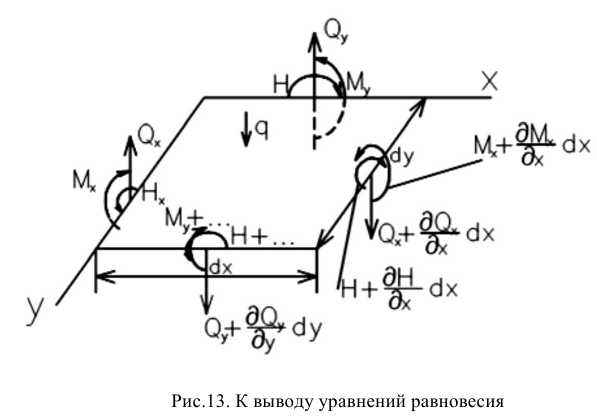
Сумма проекций всех сил на ось 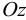должна быть равна нулю:

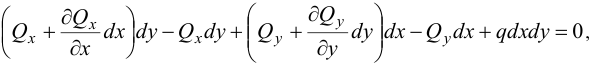
где 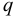— нагрузка на единицу площади. Получим:

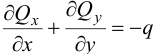
Уравнение моментов всех сил относительно :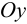

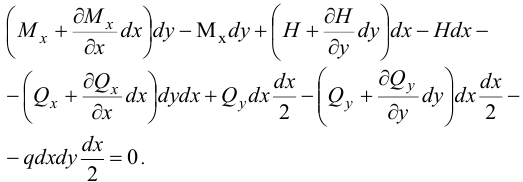
Отсюда получим (пренебрегая вторыми порядками малости):

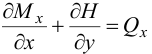
Аналогично из уравнения моментов относительно :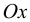

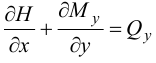
Исключая из уравнений 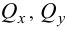, получим:

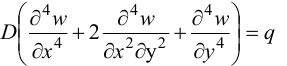
Подставив сюда выражения для моментов (23), (24) и приведя подобные, получим:

Обычно это уравнение записывают в виде:

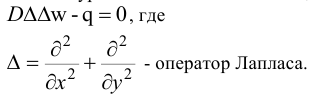
Получено основное уравнение изгиба пластины. В его решение входят произвольные функции, определяемые из краевых условий закрепления.

Формулировка граничных условий

Рассмотрим прямоугольную пластинку (рис. 14).

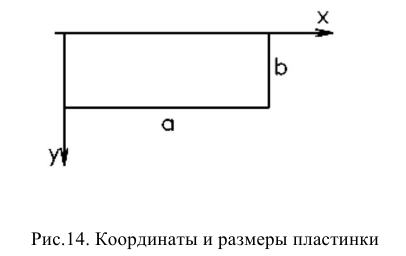
1. Защемленный край: нет ни прогибов, ни поворотов:

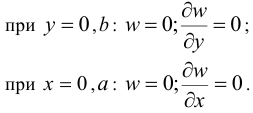
1. Шарнирно опертый край:

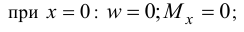
Выразим момент через прогиб

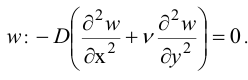
Однако при

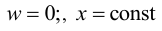
тождественно выполнено равенство

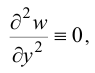
поэтому для шарнирно опертой пластинки:

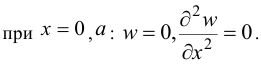
Аналогично получим:

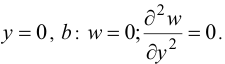
Определение. Дифференциальное уравнение в частных производных с заданными на границе области соотношениями для искомых функций называется краевой задачей.

Изгиб круглой пластинки

В полярных координатах 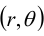оператор Лапласа имеет вид:

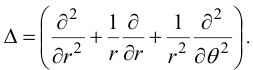
Уравнение изгиба инвариантно относительно координат:

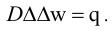
В полярных координатах:

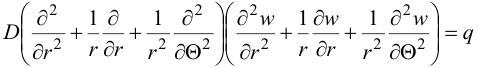
Пусть нагрузка на пластинку и условия закрепления не зависят от координаты 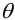. Тогда уравнение имеет вид;

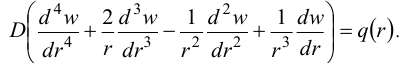
Изгибающие моменты при этих условиях равны:

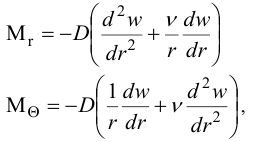
Для свободно опертой по краю пластинки краевые условия будут:

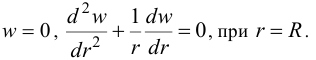
Прямой подстановкой можно проверить, что функция:

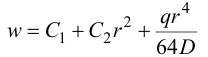
является общим решением (*) при

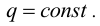
Из (**) можно найти значения произвольных постоянных :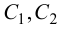

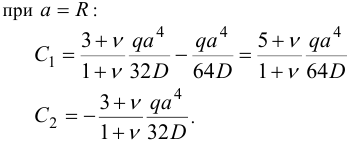
Отсюда для прогибов получим:

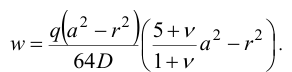
Максимальный прогиб, очевидно, в центре пластинки при :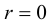

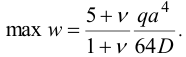
Подставляя 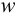в формулу для моментов, получим:

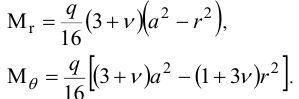
Это — параболические функции. Максимальные моменты — также в центре:

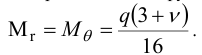
Аналогично из краевых условий

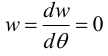
можно найт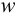и и 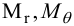для защемленной по краю пластины.

Равновесие прямоугольной пластины

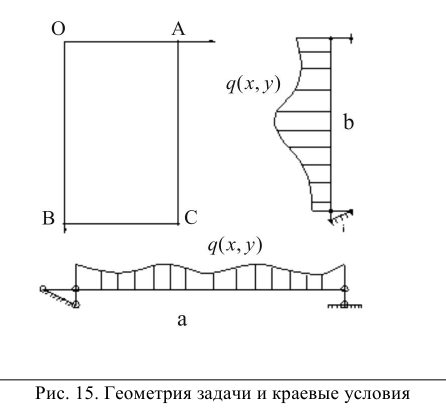
Рассмотрим шарнирно опертую по краю пластинку. Для нее краевая задача имеет вид:

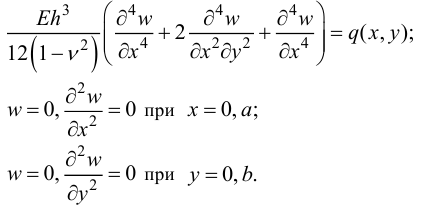
Решение ищем в виде двойного тригонометрического ряда:

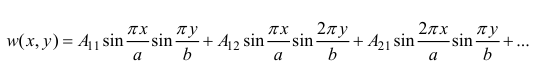
В математической теории упругости применяют сокращенную запись:

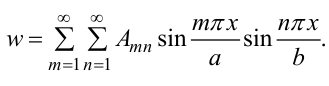
Задача сводиться к определению коэффициентов 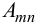. Ряд (27) удовлетворяет краевым условиям в силу того, что

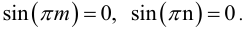
Для определения 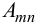надо разложить нагрузку 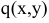в ряд, аналогичный (27), найти производные от 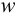, подставить все эти данные в уравнение (26) и сравнить эти коэффициенты при одинаковых тригонометрических функциях слева и справа. Сделаем это:

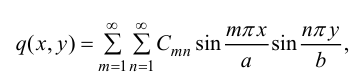
где 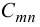известно из курса математического анализа. Собирая все результаты, получим:

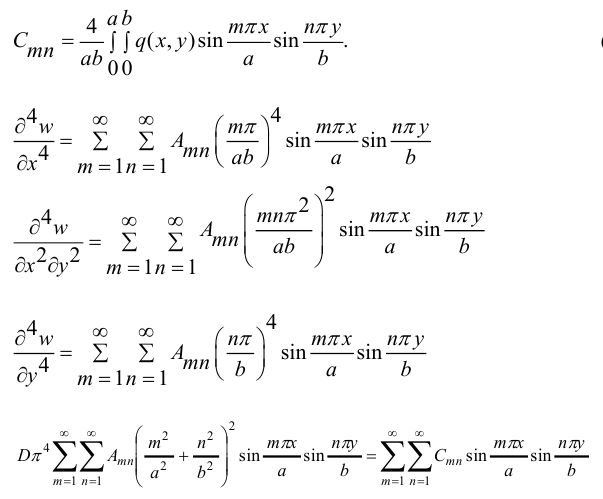
Сравнивая левую и правую части, получим:

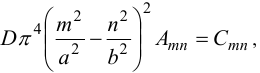
откуда

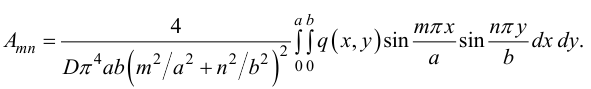
Таким образом, функция (27) полностью определена. Частные случаи: 1) Нагрузка равномерно распределена по поверхности, :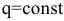

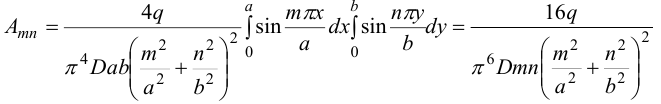
при нечетных 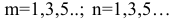(при четных индексах интеграл обращается в ноль).

Подставляя 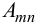в решение (27), получим:

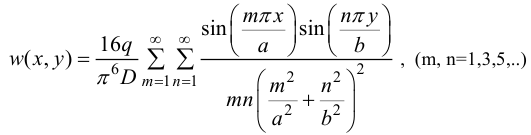
Изгибающие моменты выражаются через прогибы по формулам:

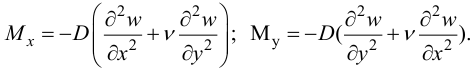
Вторые производные равны:

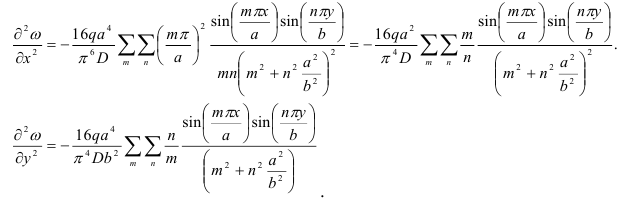
Подставляя эти выражения в формулы для моментов, получим:

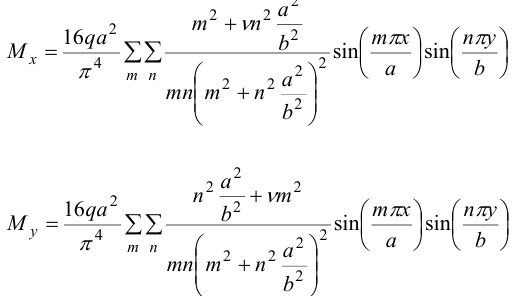
Максимальные изгибающие моменты возникают в центре пластины при

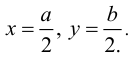
Для составления таблиц их представляют в виде:

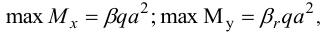
где 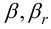— функции отношения 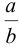. Ряд (30) сходится медленнее, чем (29), так как степень числителя выше.

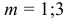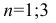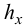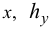Эпюры изгибающих моментов получаются табулированием функций (30). Для их построения надо оставить 4 слагаемых в ряде, т.е. члены для значений , и табулировать (30) с шагом по по 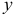. Ошибка при этом не превышает 3% от точного значения.

2) Сила 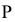сосредоточена в точке 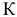с координатами 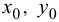. Тогда, используя 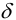— функцию, получим:

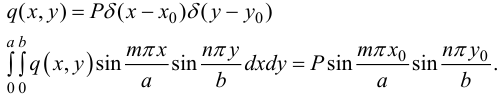
Тогда для прогибов получим:

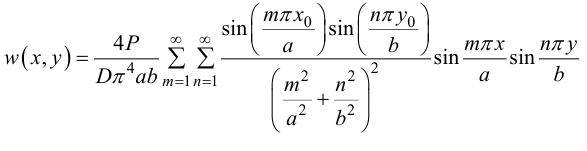
Этот ряд сходиться медленно, ряды же для 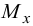и 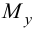сходятся еще медленнее. Поэтому эту методику можно использовать в данном случае только для нахождения прогибов. После определения 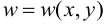можно на компьютере численно найти 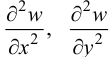и построить эпюры изгибающих моментов.

Применение вариационных принципов к расчету пластин

Энергия тонкой пластинки

При

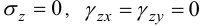
формула для удельной энергии деформации принимает вид [6]:

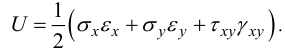
Вспоминая формулы для напряжений и деформаций

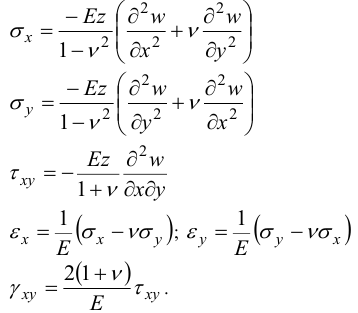
получим

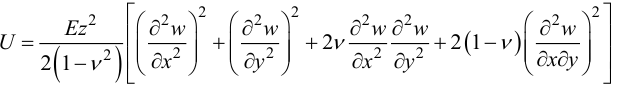
Энергия всей пластинки:

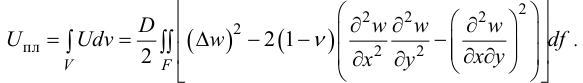
Потенциальная энергия растянутого стержня:

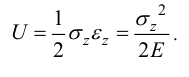
Вариационные принципы при расчете пластин

При исследовании задач теории упругости часто используют вариационные методы. Варьирование функции — операция, похожая на дифференцирование. Подробно об этой операции можно узнать из [5]. Вариационные методы часто называют энергетическими, потому что они основаны на понятиях работы сил и энергии деформации.

Принцип возможных перемещений: разность между работой внешних сил и полной энергией деформации твердого тела минимальна только на действительном перемещении этого тела.

Математически это означает, что деформация тела, имеющая место в действительности, минимизирует разность:

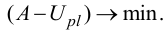
При изгибе пластинки работа внешних сил равна:

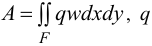— внешняя нагрузка, 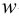— прогиб пластинки. Потенциальная энергия получается после интегрирования 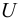по всей площади пластинки:

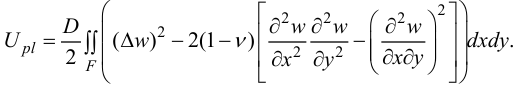
Если выбрать вид функции прогиба:

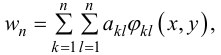
где 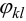— известные функции, удовлетворяющие граничным условиям, то условие минимальности примет вид:

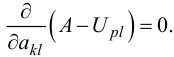
После этих выкладок становится ясен алгоритм решения задачи о равновесии пластинки (метод Ритца):

1. Задаем базисные функции .
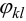2. Находим выражения для .
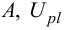3. Из условия (35) получим 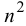уравнений для неизвестных коэффициентов 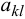. Это будут линейные алгебраические уравнения.
4. Найдем 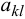и подставим в выражения для прогиба пластины 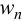, решив тем самым задачу.

Подробно этот метод изложен в учебнике [8].

Пример расчета пластинки с использованием принципа минимума энергии деформации.

Рассматривается задача о растяжении в своей плоскости прямоугольной пластинки напряжениями, приложенными вдоль ее краев по параболическому закону (рис. 16).

Пластинка растянута усилиями:

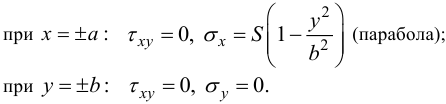
Нагрузка вдоль оси, перпендикулярной плоскости пластины, равна нулю, поэтому

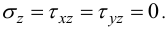
В учебнике [10] утверждается, что энергия деформации пластинки единичной толщины в этом случае равна:

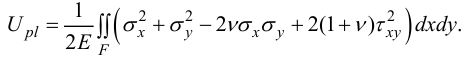
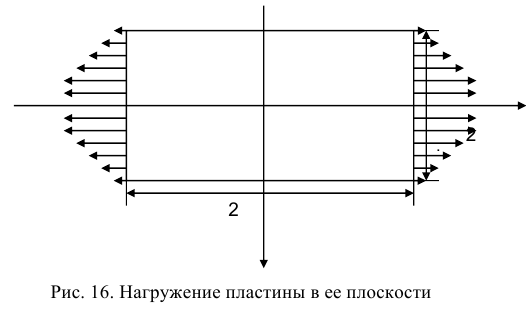
Так как распределение напряжений в прямоугольной пластине не зависит от упругих констант материала, положим в (36) 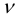= 0. Введем функцию напряжений 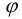следующим способом:

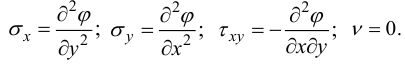
Тогда энергия пластинки выразится через функцию напряжений:

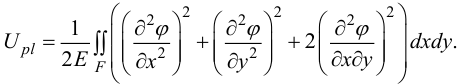
Функцию напряжений будем искать в виде:

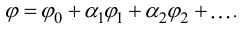
При этом все 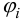должны удовлетворять краевым условиям, а коэффициенты 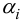находим из условий

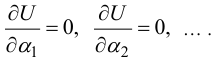
Пусть

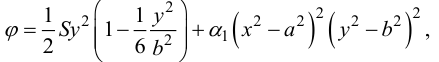
при этом краевые условия выполнены. Тогда получим уравнение для неизвестной :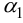

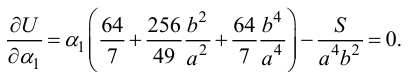
Для квадратной пластинки со стороной :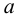

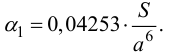
Зная 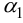, можно определить неизвестные напряжения. Фактически при решении этой задачи использован метод Ритца.

Эти страницы вам могут пригодиться:

1. Решение задач по прикладной механике
2. Курсовая работа по прикладной механике
3. Помощь по прикладной механике
4. Заказать работу по прикладной механике