Контроль при вычислениях

Контроль при вычислениях

• Расчет управления Получение необоснованных результатов за ошибки, и Если результаты появляются, все работы должны быть переделаны Я ошибаюсь Расчет должен контролироваться симплексным методом.

• Предположим, что начальный базис образован вектором ASv A5 £, …, A5. Давайте решим соответствующий симплекс В таблице есть столбец k и строка g. Тогда с новой базой ASL— ・ $ $ _ ASr + u …, ASm9Αι, векторный вид, (/ = 1, 2, …, л) Следующее разложение (формулы P, 3, 5): Λ7 = Σ (* = 2ift) / — ^ 2. (ft). (9) гк Где 2i (fe) — сумма элементов столбца разрешения kf 2 Рассчитано так же, как ^ ·.

Разложите все векторы исходной системы вдоль этого базиса. м Ai = 2 * Α ・ ρ / = 1. 2f …, η- (Ι) Людмила Фирмаль

Так правильно Уравнение (8) может быть получено согласно уравнению (9). Нормальное преобразование по формуле, чтобы полностью исключить суммы Si ** для обозначения суммы всех элементов решения Столбцы таблицы до 2s> m0, уравнение (8) принимает следующий вид: Σ1 * -2nd *. (U)

Так что для всех столбцов без исключения Симплексный стол с аналогичными условиями управления (7) (10). Суть их в прямо рассчитанном количестве Каждый элемент столбца должен быть равен преобразованному. На практике они обычно делают это. Оригинал полон Выберите симплексную таблицу и ее элементы разрешения. ниже Каждый столбец записывает соответствующую сумму.

Для этого в таблицу добавляется специальная строка. | ς. Σί0) Σι » … ςΗ В следующей таблице также представлены три строки. Σ2, яз. Исходная таблица со строкой Σι трансформируется Обычным способом. Результат преобразования строки символов Σι записывается К строке Σ2 новой таблицы.

После окончания Преобразование исходной таблицы, все элементы каждого суммируются Столбец основной части симплексной таблицы (без строк Σι, Σ2) Найденная сумма записывается в строку Σ3. Строки Σ2 и Σ3 Должно быть то же самое g. Учитывайте точность расчета. Это Вы также можете контролировать точность новых таблиц расчетов.

Если при заполнении таблицы выше ошибок нет Если разрешено, удобно контролировать следующую таблицу Сделайте следующее: 1) Выберите строку (d) и столбец (S), которые необходимо разрешить, (2) o Имея это в виду, введите строку Σι. При вводе строки Σι удобно использовать строку Σ3.

• Для этого вычтите элементы из каждого итога 3 Для строк разрешения и направляющих столбцов, Направляющие элементы — 1: ΣΨ = ΣΡ- * «\ / φ * ΣΤ-ΣΡ — *» — 1. 00 Новое после ввода строки Σι Симплекс таблицы для преобразования в соответствии с полной формулой исключения, и Линия Σline В этом случае линии Σ2 и Σ3 не изменяются. Контрольный расчет для новой таблицы выполняется аналогичным образом.

Аналогичные правила управления могут быть получены для символьных строк. Симплекс стол. Формула расчета отличается в следующих пунктах Элемент решения Σί количества строки решения Заменяется на +1. Аналогичным образом три столбца Σι добавляются в таблицу, Ez.

Одновременное управление симплексными столбцами и строками Поскольку размер таблицы значительно увеличивается, Практика обычно делается только для выявления ошибок. Людмила Фирмаль

Как правило, контроль столбца или Линия. Более выгодно контролировать столбцы. Это естественно В результате преобразования симплекс таблицы Может отображаться большое количество нулевых столбцов. Необходимость удаления такой колонки очень сложна Струнный контроль.

Кроме того, вы можете: Рекомендуется в конце определенных этапов и расчетов 1) Замена компонентов основного решения поставленной задачи Все ограничения, все ограничения 2) Рассчитать значение целевой функции для сравнения Получил за столом. Рассмотрим пример задачи линейного программирования.

Решить симплекс-методом с контролем столбцов Таблица. Пример. Найти максимальное значение функции Ζ = 4xj + xa + x3- * 4- * глах В условиях 2xi + * 3 + * 4 = 20 ‘4J4-2×2 + 2 * 3 «16 (* /> ° / β1» 2.-… 4). Уменьшите эту проблему до стандартной формы и напишите немедленно Соответствующая ему Λ-задача: определить минимальное значение функции (—Ζ) = -h-4×1- — * 2 «- * 3 + * 4 + Mxb- * мин Под ограничениями 2x {+ Xs + x4 == 20 ‘> 4 * 1-2 * 2 + 2 * 3 + * 5 = 16; * /> 0, / = 1, 2, …, 5.

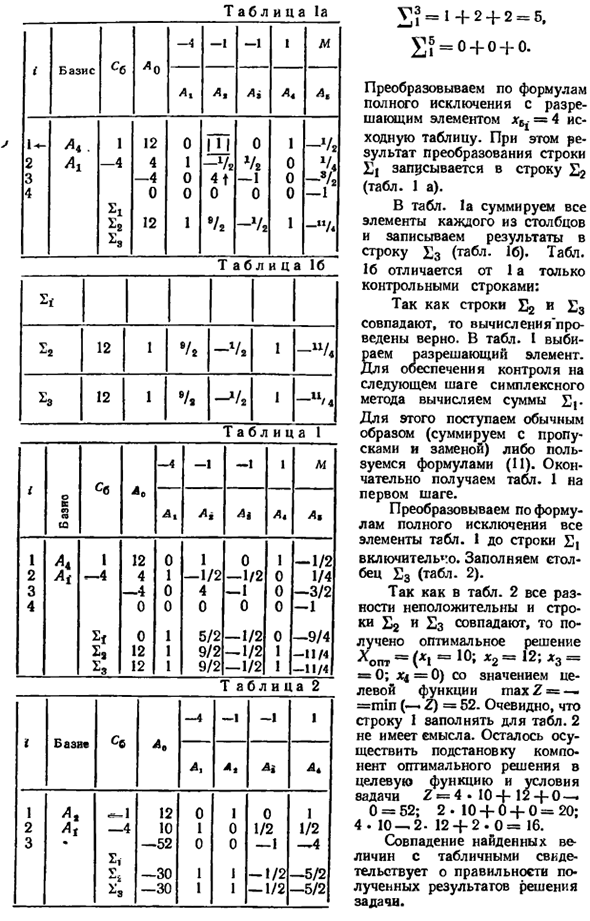
Введите оригинал (ноль) Таблица. Подведите итог после выбора Элемент авторизации Известные правила содержания Каждый столбец и Запишите результат в строку Σι. £ 0 = 20 + 20 + 16 = 56, £? = 0 + 1-2 1, Σϊβ— i + o + o —ι. Σϊ = 2 + (_Ι) + 6 + 4 = 11, Конвертировать с формулой И полное исключение Разрешение элемента lgB = 4 Исходная таблица.

В то же время Результат преобразования строки Σι записывается в строку Σ2 (Таблица 1а). В таблице. Подведите итог 1а Каждый элемент столбца Напишите результат Строка Σ3 (Таблица 16). Tab. 16 отличается от 1а только Контрольная линия: Потому что линии £ 2 и £ 3 Рассчитать после сопоставления Сделано правильно. В таблице. Я Выберите элемент разрешения.

Обеспечить контроль Следующий симплексный шаг Метод, всего Σ \ — Из-за этого мы всегда Метод (и подвести итог Проход и обмен) Используйте уравнение (11). Наконец, получите стол. К 1 Первый шаг Конвертировать в Все выражения исключений Элемент таблицы 1 строка Σγ Всестороннее. Пожалуйста, заполните Столбец 3 (таблица 2).

Потому что это за столом. 2 все Разница не положительная, Если строки £ 2 и Σ3 совпадают, Получено оптимальное решение Hopt = (* 1 = 10; * 2 ​​= 12 ‘> * 3 = = 0; JC4 = 0) со значением Объективная функция maxΖ = — = мин (- »Ζ) = 52. Очевидно, что Строка 1, чтобы заполнить таблицу. 2

Там нет смысла. оставшийся Для того, чтобы заменить Компоненты оптимального решения Объективные функции и условия Задача Ζ = 4. 10+ 12 + 0- 0 = 52; 2,10 + 0 + 0 = 20; 4.10-2-12 + 2-0 = 16. Матч найден Табличные значения Показать правильность Результат определения Задача.

Смотрите также:

Решение задач по линейному программированию

Понятие о двойственных задачах	Контроль при вычислениях
Симплексный метод с искусственным базисом	Модифицированный симплексный метод