Контактные напряжения
Местные напряжения, возникающие при взаимном нажатии двух соприкасающихся тел, называют контактными напряжениями. Вследствие деформации материала в месте соприкосновения возникает площадка контакта, по которой и происходит передача давления. Материал вблизи такой площадки, не имея возможности свободно деформироваться, испытывает объемное напряженное состояние.
Контактные напряжения играют основную роль при расчете шариковых и роликовых подшипников, зубчатых колес, элементов кулачковых механизмов и т. д. Эти напряжения определяют методами теории упругости при следующих допущениях: а) в зоне контакта возникают только упругие деформации, следующие закону Гука; б) линейные размеры площадки контакта малы по сравнению с радиусами кривизны соприкасающихся поверхностей; в) силы давления, распределенные по поверхности контакта, нормальны к этим поверхностям; г) на поверхности контакта возникают только нормальные напряжения.
При этих допущениях нормальные напряжения по площадке контакта распределяются по закону поверхности эллипсоида, площадка контакта имеет в общем случае форму эллипса, а максимальное напряжение действует в центре площадки контакта.
Приведем без вывода расчетные формулы для некоторых частных случаев контактной задачи в предположении, что коэффициент Пуассона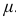 
= 0,3. Отметим, что для практических расчетов указанные формулы пригодны и при других значениях .
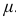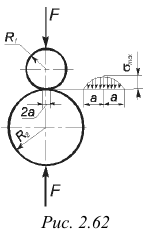
Сжатие шаров. В случае взаимного сжатия силами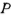 
двух упругих шаров радиусов 
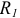и 
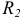(рис. 2.62) образуется круглая площадка контакта, радиус которой
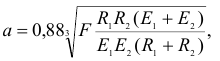
где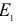 
и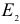 
— модули упругости материалов шаров.
Максимальное нормальное напряжение в центре площадки контакта
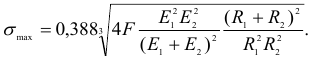
Наиболее напряженная точка находится в центре площадки контакта, где материал испытывает напряженное состояние, близкое к равномерному сжатию (главные напряжения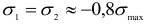 
и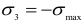 
). Опасная же точка расположена на линии действия сил 
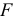на глубине, примерно равной половине радиуса площадки контакта. Главные напряжения в этой точке
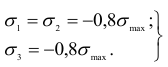
Наибольшее касательное напряжение в опасной точке
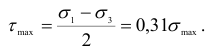
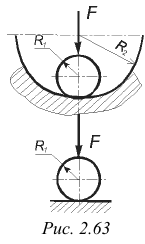
Формула (2.126) справедлива и в случае давления шара на вогнутую сферическую поверхность радиуса 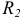(рис. 2.63, а). Изменив в указанной формуле знак при 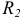на обратный, имеем
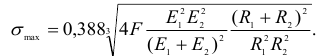
При взаимном давлении шара и плоскости (рис. 2.63, б), полагая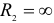 
, получим
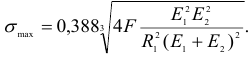
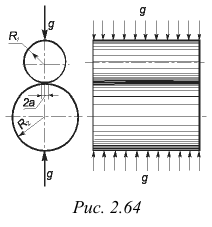
Сжатие цилиндров. Два цилиндра, соприкасающиеся по образующей (рис. 2.64), испытывают взаимное давление по всей длине линии контакта. При равномерно распределенной нагрузке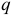 
площадка касания имеет вид узкого прямоугольника, ширина которого
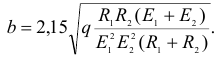
Максимальное напряжение сжатия действует в точках оси площадки контакта:
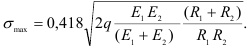
В опасной точке, расположенной на глубине, равной 0,4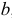
, главные напряжения имеют значения
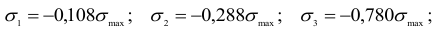
Наибольшее касательное напряжение в опасной точке
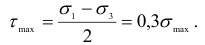
В случае давления цилиндра на деталь с вогнутой цилиндрической поверхностью значение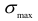 
определяют по формуле (2.132), предварительно изменив в ней знак при 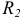на обратный. Подставив в формулу (2.132) величину 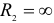, получим выражение для 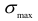в случае взаимного давления цилиндра и детали с плоской поверхностью.
На основании формул для определения 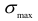нетрудно установить, что контактные напряжения не являются линейной функцией нагрузки, с ростом сил они возрастают все медленнее. Это объясняется тем, что с увеличением нагрузки увеличивается и площадка контакта. Здесь следует обратить внимание на следующее обстоятельство: если размеры площадки контакта окажутся сопоставимыми с величиной радиусов кривизны соприкасающихся поверхностей, то приведенные выше расчетные зависимости применять нельзя.
Аналогичная картина имеет место при определении контактных напряжений между поверхностью тела болта или заклепки и цилиндрической поверхностью отверстия. Местные напряжения в этом случае обычно называют напряжениями смятия и считают, что по площадке контакта (смятия) они распределены равномерно. Такой же закон распределения напряжений по площади контакта принимают и в том случае, если тела до соприкосновения имели плоские поверхности. Учитывая указанное допущение, имеем следующую формулу для определения напряжения смятия:
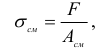
где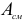 
— площадь смятия.
В расчетах на прочность допускаемые напряжения на смятие принимают (на основании опытных данных) в 2-2,5 раза больше допускаемых напряжений на обычное сжатие, т. е.
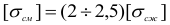
Проверку прочности при контактных напряжениях следует производить по формулам третьей или четвертой теорий прочности.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Видимые местные напряжения |
| Концентрация напряжений определение и формулы |
| Отклонения формы и расположения поверхностей |
| Принципы построения единой системы допусков и посадок |
