Оглавление:





Контактные напряжения
- Контактное напряжение Напряжение, возникающее, когда часть конструкции прижимается к другой части в точке контакта, называется контактным напряжением. Начальный точечный контакт объекта, ограниченный криволинейной поверхностью вследствие деформации, обычно соприкасается в некоторых места
х с овалом. Вблизи этого участка материал подвергается состоянию объемного напряжения. Величина контактного напряжения
очень быстро уменьшается при удалении от зоны контакта. Материал Людмила Фирмаль
по сравнению с габаритными размерами контактной поверхности, причем площадь контакта представляет собой силу давления, перпендикулярную контактной поверхности контактной поверхности, а силой трения в зоне контакта пренебрегают. Проблема контакта-это форма и размер контактной зоны тела после деформации; размер и величина давления, оказываемого одним
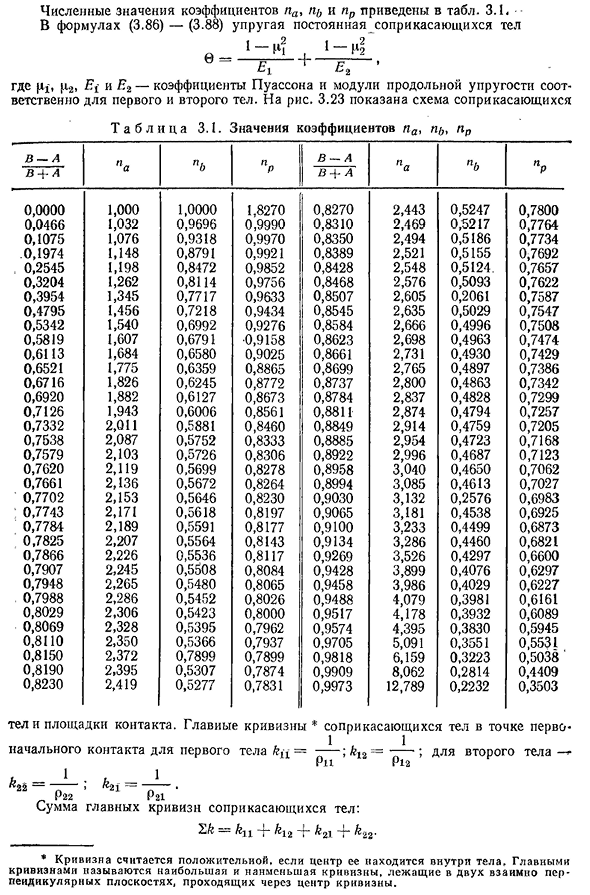
телом на другое и передаваемого через контактную зону. Размеры сенсорной панели определяются полуосями эллипса: Куда? _ _______________ Максимальное давление между контактами определяется по формуле: 4/4 (4-гр- Куда? Один. ’PA Pi сходимость континуума в результате их преобразования: K= — T®2™*, (3.88) Куда? з G4PA=а / ——— ———— — , г>™(л+4) Численные значения коэффициентов PA, P/} и PR приведены в таблице. 3.1 Уравнение
- (3.86) — (3.88) упругая постоянная континуума Где pt, C2, Ef и E2-коэффициент Пуассона и продольный модуль первого и второго объектов соответственно. 3.23 показана схема касания Т А Б Л и с А3. 1. Значение коэффициентов PA, p^, PR И п п’п В-и п НХ п В+А А Р+А А А Р 0,0000 1,000 1,0000 1,8270 0,8270 2,443 0,5247 0,7800 0.0466 1.032 0.9696 0.99 0.8310 2.469 0.5217 0.7764 0.1075 1.076 0.9318 0.99 0.350 2.494 0.5186 0.7734 0.1974 1.148 0.8791 0.9921 0.8389 2.521 0.5155 0.7692 0.2545, 1.198 0.8472 0.9852, 0.8428 2.548, 0.5124. 0.7657 0.3204 1.262 0.8114 0.9756
0.8468 2.576 0.5093 0.7622 0.3954 1.345 0.7717 0.9633 0.8507 2.605 0.2061 0.7587 0.47595 1.456 0.7218 0.9434 0.8545 2.635 0.5029 0.7547 0.5342 1.540 0.6992 0.9276 0.8584 2.666 0.4996 0.7508 0,5819 1,607 0,6791 •0,9158 0,8623 2,698 0,4963 0,7474 0.6113 1.684 0.6580 0.9025 0.8661 2.731 0.4930 0.7429 0.6521 1.775 0.6359 0.8865 0.8699 2.765 0.4897 0.7386 0,6716 1,826 0,6245 0,8772 0,8737 2,800 0,4863 0,7342 0,6920 1,882 0,6127 0,8673 0,8784 2,837 0,4828 0,7299 0.7126 1.943 0.6006 0.8561 0.8811 2.874 0.479 0.7257 0.7332 2.01 0.5881 0.8460 0.8849 2.914 0.4759 0.7205 0,7538 2,087 0,5752 0,8333 0,8885 2,954 0,4723 0,7168 0.7579 2.103 0.5726 0.8306 0.8922 2.996 0.4687 0.7123 0,7620 2,119 0,5699 0,8278 0,8958 3,040 0,4650 0,7062 0,7661 2,136 0,5672 0,8264 0,8994 3,085 0,4613 0,7027 0,7702 2,153 0,56 0,8230 0,9030 3,132 0,2576 0,6983: 0.7743 2.171 0.5618 0.8197 0.9065 3.181 0.4538
0.6925 0,7784 2,189 0,5591 0,8177 0,9100 3,233 0,4499 0,6873 0,7825 2,207 0,5564 Людмила Фирмаль
0,8143 0,9134 3,286 0,4460 0,6821 0.7866 2.226 0.5536 0.8117 0.9269 3.526 0.4297 0.6600 0.7907 2.245 0.5508 0.8084 0.9428 3.899 0.4076 0.6297 0.7948 2.265 0.5480 0.8065 0.9458 3.986 0.4029 0.6227 0,7988 2,286 0,5452 0,8026 0,9488 4,079 0,3981 0,6161 0.8029 2.306 0.5423 0.8000 0.9517 4.178 0.3932 0.6089 0.8069 2.328 0.5395 0.7962 0.9574 4.395 0.3830 0.5945 0,8110 2,350 0,536 6 0,7937 0,9705 5,091 0,351 0,5531 0.8150 2.372 0.7899 0.7899 0.9818 6.159 0.3223 0.5038′ 0,8190 2,395 0,5307 0,7874 0,9909 8,062 0,2814 0,4409 0,8230 2,419 0,5277 0,7831 0,9973 12,789 0,2232 0,3503 Тело и площадь контакта. Основная кривизна первого контакта для первого тела k a= * Контакт с телом во время первого 1. Один. 7— 5 ^12 = 7;— ’> для второго тела —* П Лл Р12. 1. B_1 и 2 2р Р22 ′ 2 1П2 1 Сумма первичной
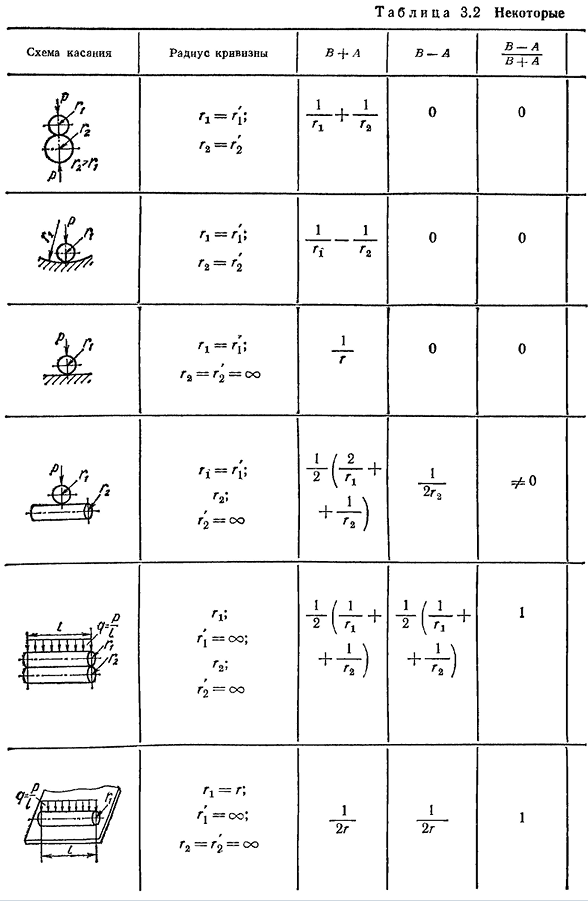
кривизны контактного тела: ГИА—ф — &12-Ф-fe21-Джей — & 22 Кривизна считается положительной, если ее центр находится в теле. Главные кривизны — это максимальная и минимальная кривизны в двух плоскостях, перпендикулярных друг другу через центр кривизны. 53T ABL и C a3. 2 часть Схема касания радиус кривизны B4-a b-A B-A B+A £г, р, я=<; Г2=Г2 1+1 G1G2 Ноль. Ноль. Ри=/•[; Г2=г’ 1-1 Р и Г2 Ноль. Ноль. К Пи! Г2-Г2-ОО Один. Г Ноль. Ноль. Р Я=Г; Г2- Г2=со + ’. ) Один. 2ga Ноль. Один. 1pthh — Г» R’I=o o ; Г2=<х> — г(тг+ Отчет Один. 54 случая телефонного контакта Сенсорная панель a эллиптическая полуось, B максимальное контактное давление RM A-C тело a конвергенция Ка-пи-1; В4(Г1+Г2) «р=я; — i/J
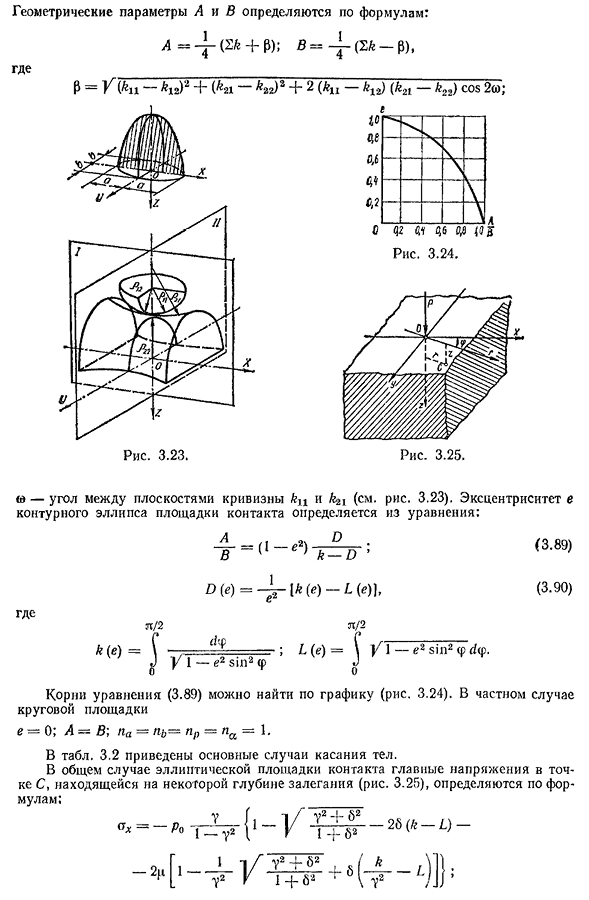
E E E П в(РТР^02-г/тр^е!’» ПР=1; Но 1 1Z6P (f2 -*■? Л? (r1P2)2 02 — О!; 2? 2 ВХ ПР=1;1/~6Р » 2В — О!;1 902R2 2Г Ия у=1;ПИ Ф1; тебя 1 / ■3КВ^П Н А В2(2r2+Р Т) 1,Вт/»3 0г/2П Б=, ЛБ-П#К т Р=£1; п а ’ /902R2(2G2+ГТ) 2V4g1g2 1/р(р+Г2) в lghg2v1 2Р НЛ \1-J4 не+0.407 J в+ — Х Х(в^р-+0.407^ ♪Сто одиннадцать♪ Р nrQl Гидрогеометрические параметры A и B определяются по формуле: 4=-^(С Ф С+П); Б=_l, за (2fe_p) я Куда? Р-У (&Я^ИА)2~ь(&21^гг)2~В2(£С К12)(&21-^22) со s2so; Ш)= — ^ — [Ф С (Е) — £(Е) Л(3.90) Куда? П/2Л/2 К (Е)=\ -. ■;£, (е)=\У1-E2sin2mdm. Джей У1-E2sin2 Корень уравнения(3.89) находится на графике(рис. 3.24). В частном случае круговой платформы e-0, A=B; PA-PI=PR=PA=1. За столом. 3.2 приведены основные случаи, которые касаются тела. В общем случае
эллиптической контактной области Главное напряжение находится в точке с, расположенной на определенной глубине(рис. 3.25) определяется по формуле: — O.-4 4{1-u» — o — Ирис 3.26 —— T / VI7 ША Где v= -, 6= -, RA-давление в центре сенсорной панели, а k и L-полный эллиптический Интеграл. Система координат выбирается таким образом, чтобы оси x и y совпадали с полуосями a и b Овального контура сенсорной панели. Самое большое касательное давление, TM axdao, 325ro, и круговой случай сенсорной панели (a-bj) специальный для Т Макс=о>31 Ро- Прочность контактного тела
проверяется по наибольшему расчетному (приведенному) напряжению. За столом. 3.3 В зависимости от соотношения между полуосями эллипса в месте контакта приведены расчетные значения напряжений, соответствующие III и IV теории прочности. Например. Определите допустимую осевую нагрузку [Q], размер площади контакта и величину схождения колец в упорном шарикоподшипнике с плоскими кольцами(рис. 3.26), радиус шарика g-5 мм, количество шариков I=20, материал шарика и кольца-хромистая сталь. Допустимое давление в месте
контакта[Rmax]=3000 МПА (30 000 кгс / см2). Решение. Для определенной схемы прикоснитесь к столу. 3.2 найти максимальное контактное давление ^Макс L’l20a Или 0=2 в Т Макс=0.3883 П£а ( Нагрузка оптического шарика становится Р—, где 0,8-коэффициент неравномерного распределения нагрузки подшипника между отдельными шариками. RE2 Затем напишите p^ako=0,3883 —. Если предположить, Rмакс=[Rмакс]=3000MPa а б л и Ц А3.3. Расчетная величина напряжения б о и в пиар пиар Ро Ро 1-00-круг 0.620 0.620 0.75] 0.625 0.617 0.50 1-овалы 0.649 0.611 0.20 ) 0.646, 0.587 0, 0 0—диапазон 0,600 0,557(30000kgf / cm2), получает емкость подшипника [Вопрос=] [^Макс!3 0, сэр «30 000». 0.8 мин 20.0.5 «0.388 » E» 0,388″ (2,12 • 10°)2 =4,13 кн (413 кгс), Один мяч будет принимать нагрузку З-Б Д Г=° ’ 26kN<26kgf>- Радиус контактной зоны (окружность): Упругая конвергенция шарика и кольца: «= 1,231 / (-£ -)’ 4 — — 1.231 0,00033 смотреть Кольцо конвергенции 2A=0.00166 см.
Смотрите также:
| Толстостенные цилиндры | Сдвиг. основные положения |
| Напряжения в составных толстостенных цилиндрах | Расчеты на прочность |

