Пример задачи 8.7
Консольный стальной брус (рис. 8.15, а) круглого поперечного сечения диаметром d = 40 мм нагружен системой внешних сил.
В опасном сечении бруса построить эпюры нормальных и касательных напряжений, отыскать его опасную точку.
Проверить прочность стержня, если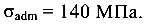 
Решение
Сосредоточенная сила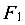 
, действующая перпендикулярно к продольной оси бруса Z, подвергает его плоскому изгибу в вертикальной плоскости, а сила 
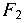— в горизонтальной.
Момент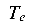 
, действующий вокруг продольной оси бруса Z, скручи-вает его.
Совместное действие всех внешних сил подвергает рассматриваемый брус изгибу с кручением.
В сечениях бруса образуются усилия — изгибающие моменты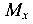 
, 
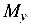и крутящий момент Т, эпюры которых приведены на рис. 8.15, б, в, г.
Анализ эпюр показывает, что опасным является опорное сечение (защемление), где все три усилия наибольшие:
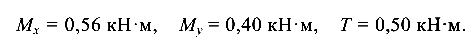
Для проверки прочности бруса воспользуемся формулой (8.9)
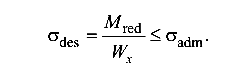
По четвертой теории прочности приведенный момент в опасном сечении бруса
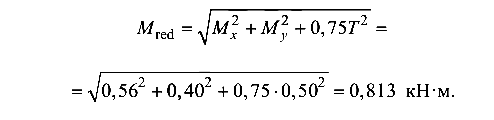
Осевой момент сопротивления для круглого сплошного сечения
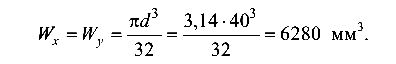
Расчетное напряжение
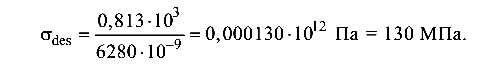
Условие прочности рассматриваемого бруса выполняется, так как
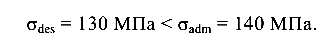
Приступим к определению наибольших нормальных и касательных напряжений в опасном сечении бруса.
Нормальные напряжения от изгибающих моментов, действующих в главных плоскостях бруса:
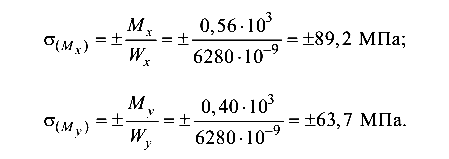
Наибольшее касательное напряжение от крутящего момента Т, действующее в любой точке контура сечения:
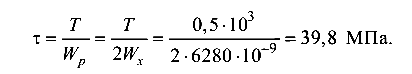
Положение нейтральной оси определяем по формуле (8.1):
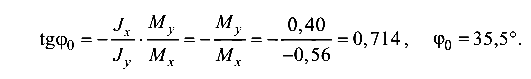
Напомним, что для круглого сечения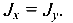 
Угол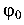 
откладывается от оси X против хода часовой стрелки.
Суммарный изгибающий момент в опасном сечении бруса
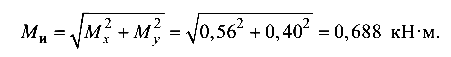
Экстремальные нормальные напряжения от суммарного изгибающего момента
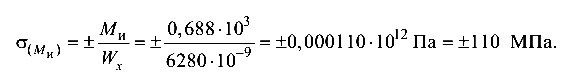
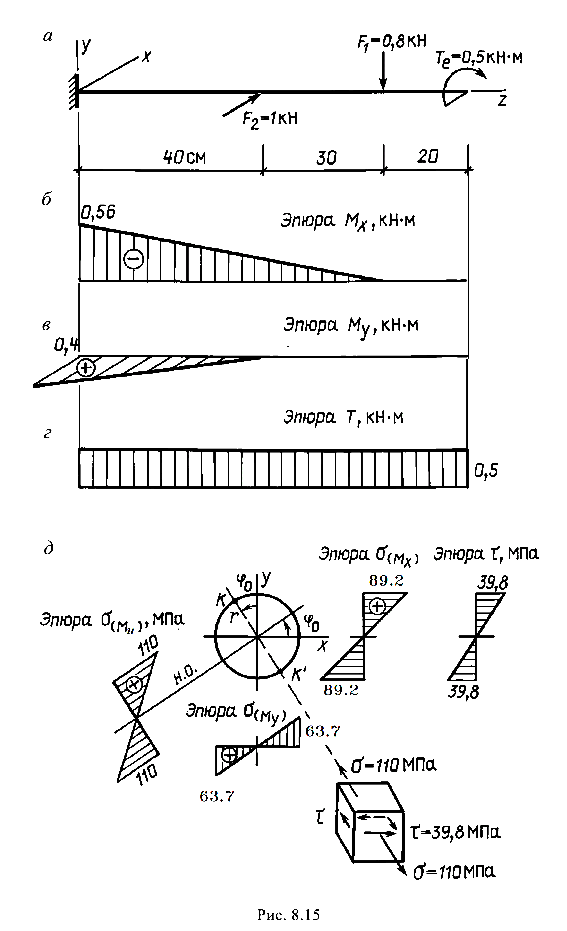
Эпюры нормальных а и касательных т напряжений показаны на рис. 8.15, д.
Анализ эпюр напряжений показывает, что наиболее напряженная точка лежит на контуре сечения, где нормальное напряжение от суммарного изгибающего момента максимально. Это точка К, лежащая по линии, перпендикулярной нейтральной оси, или ей противоположная К’. Координаты точки К определяются по радиусу r и соответствующей тригонометрической функции.
Напряжения, действующие по граням элементарного прямоугольника, выделенного вокруг точки К,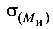 
и 
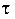показаны на рис. 8.25, д.
Исходя из 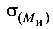) и 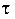, несложно вычислить главные напряжения 
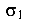и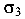 
и убедиться, что при изгибе с кручением материал бруса находится в условии плоского напряженного состояния и проверку прочности можно провести, используя главные напряжения.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
