Оглавление:


















Конические зубчатые передачи
- Коническая шестерня Основная информация. Коническое зубчатое колесо использовано в передаче где оси вала пересекают под некоторым направлением.- Наиболее распространена передача с углом 124, 2, 2=90°, передача конической формы сложнее цилиндрической в изготовлении и монтаже. Для резки конического колеса требуются специальные станки и инструменты^пересечения валов затрудняют размещение опор. Одно из конических колес, как правило, расположено на кантилевере. В этом случае неравномерное распределение нагрузки по длине зубьев увеличивается, а в коническом зацеплении действуют осевые силы, что усложняет
конструкцию опор. Все это приводит к тому, что грузоподъемность конусообразной передачи составляет около 0,85 по сравнению с цилиндрической. Несмотря на указанные недостатки, конические зубчатые колеса применяются очень широко, поскольку в конструкции станка необходимо располагать вал под углом. Типы конических зубчатых колес и их характеристики. Конические зубчатые колеса различают между прямыми, косыми(тангенциальными) и круговыми зубьями (см. рис. 4,1, e, f, C). Касательные зубья (рис. 4.39, а) тангенциально направлена к некоторой воображаемой окружности радиуса е и образует с конической формой угол р. 4.39, б)
расположена на дуге, по которой инструмент перемещается при резании зуба, причем угол наклона Людмила Фирмаль
кругового зуба является переменным. Величина угла Р30* — для колес с тангенциальными зубьями и РТ-35* — для колес с круглыми зубьями. В чашах используются конические колеса с круглыми зубьями, которые имеют ряд преимуществ. 125 белка 4.40 Габаритные размеры имеют более высокую несущую способность;при увеличенной окружной скорости (до 11 м/с с неокрашенными зубьями и до 35 м / с с полированными)габаритные размеры регулируются. Конические зубья колеса, исходя из изменения размеров детали по длине зубьев, образуют три формы. Форма I-пропорциональное уменьшение зубьев (рис. 4.40, а). Вершины и вмятины делителя совпадают. Высота ножки
зуба пропорциональна расстоянию до конуса; эта форма является основной для прямозубых и конических зубчатых колес. Он также использован для шестерен с круговыми зубьями на zs=20… Сто Форма I I-выпадающие зубы(рис. 4.40 б, д). Вершины и вмятины делителей не совпадают. Ширина дна полости постоянна,а толщина зубьев вдоль разделительного конуса увеличивается пропорционально расстоянию от вершины. Эта форма позволяет обрабатывать обе стороны зуба одним инструментом одновременно. Он является основным для колес с круговыми зубьями. Форма I I I-зубцы одинаковой высоты(рис. 4.40, в). Генераторы делителей конусов, вмятин и вершин параллельны. Эта форма использована для
- круговых зубов zs40. Для прямых зубчатых колес конической формы с зубьями в виде 1, Как правило, выбирают стандартное значение модуля внешней окружности mte и имеют круговое колесо на внешнем конце, что удобно для проведения измерений. 126зубями обычно выбирают стандартное значение обычного модуля TP и размер зубьев в середине ширины зубчатой передачи (хотя это необязательно). Если зуб I обычно работает в форме окружности внешнего шага (наружного конца), а зуб II (в середине ширины коронки) и больной имеют средний индекс окружности. Поскольку подрезка отсутствует, минимальное количество зубьев, разрешенных к использованию, показано в таблице. 4.17 Вы также можете использовать формулы для определения минимального количества
зубов 4.17 минимальное количество зубьев зубчатого колеса Передаточное число G1PR“ О…i5°20…25 ° 30…40° Один. 17 17 17 17 1,6 15 15 14 Два. 13 12 11 3, 15, 12, 10, 8. 21mln17COS COS3 0, где угол зубчатого раздельного конуса. В практике проектирования рекомендуется выбирать GC»=! 18…30, в то время как в течение минуты пара прямых зубов 25,для пары с круглыми зубьями GG минута 15. Производственный размер конического колеса — это размер нормального сечения, обычно на большом конце, выраженный через внешний окружной модуль.
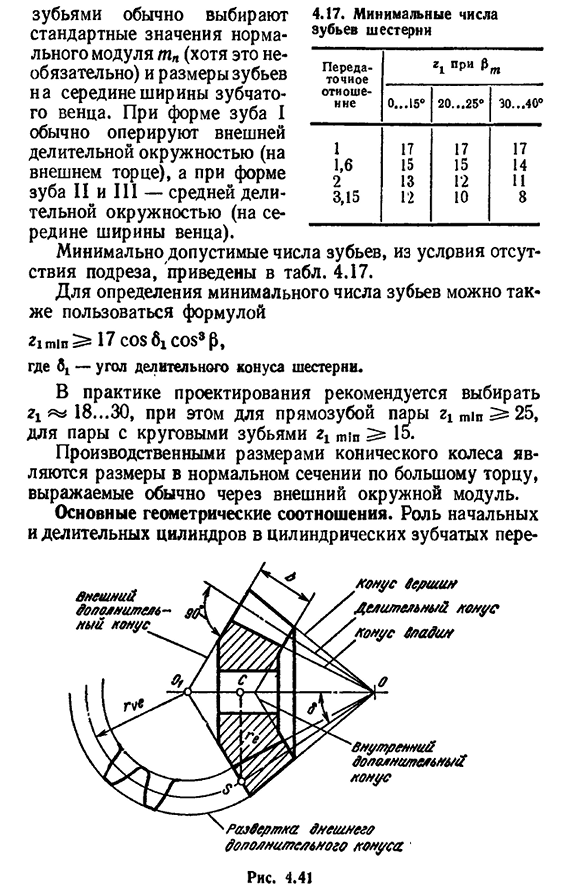
Основные геометрические соотношения. Роль начального и делительного цилиндров в цилиндрической передаче- ооолит-д В Стреловидность внешних дополнительных Людмила Фирмаль
конусов Внутреннего дополнительного конуса Рис 4.41 Г / Конус пика, который делит конус впадины 127дачах выполнить начальный и расщепленный конус(рис. 4.41). В конических зубчатых колесах начальный и разделительный конусы всегда одинаковы. Углы раскола конусов указывают, соответственно, и на 62. Угол между осями 2=6! + B2 эвольвентный зуб конического колеса профилирован со стреловидностью дополнительного конуса, образующая часть которого перпендикулярна образующей части расщепленного конуса. Дополнительные конусы могут быть построены для внешней, средней и внутренней секций углового колеса. Ширина венца зубчатого колеса б ограничена двумя дополнительными конусами внешним и внутренним. Длина зубчатого модуля и соответственно высота
являются переменными. Для удобства измерения конических колес их размеры обычно определяются наружным концом зуба, который образован внешними дополнительными конусами. Максимальный модуль упругости зуба Te-это периферийный модуль, полученный на внешнем конце, иногда называемый производственным модулем упругости. Он обычно округляется в соответствии с ST SEV310-76. Внешний диаметр деления (рис. 4.42). tTlgZ»» 128 нормальный руководитель обручальное высота и высота ножки соответственно Хэ=тригонометрию, быстро,=1, 2fne. Наружный диаметр вершины зуба dae=dej-2=cos6. Расстояние внешнего конуса (см. треугольник ACS) R e=y y, если+T=Y^Y или R e = deJ(2sin61) = meZi/(2sin6J. Среднее
расстояние конуса R=re-0,5 b. Угол ножки зубьев tg=hfe / R e. По ГОСТ 19624-74ба1=6ф2; 0е2=0З1; где 0е-угол наклона головки зуба. Средний деленный диаметр шестерни di=m il = del-b sin6i=dei-b/Y » a+1, (4.34) Где b-ширина обода колеса. Разделив левую и правую части формулы (4.34) на zt, получим средний модуль зуба zn=/nf-(&sin6i)/Zi. (4.35)передаточное число. Угол деления (первый) конуса BX и 62 связаны с передаточным отношением таким же образом, как и
конические фрикционные шестерни. В 2=90°можно записать»12=dcildei=2Re sin 62/(2/?e sin6i)=sin62 / s in6i. Если мы выражаем 62=90° — 6X, то: «и=sin (90° — 6i)/sin6i = ctg6i, соответственно 6X=90° — 62″12=sin62 / sin(90° — 62) = tg62. Таким образом, передаточное отношение может быть выражено как » 12=(O1/o) g=dg Для конических зубчатых колес рекомендуется M12=2…3; в колесе с непрямыми зубьями I возможно высокое значение] 2; I12=6,3, большее значение (по ГОСТ12289-76). Усилие в зацеплении передачи Прямой конической формы. В зацеплении конической передачи действует сила: Окружная Ft, радиальная Fr и осевая Fa. Зависимость между этими силами устанавливается рисунком. 4.43, где тяговое усилие приложено к
шестерне. Сила, действующая на нормальные зубы Fn, распадается на Fn и f’R. В свою очередь, F’N разбирается на Fai и Fn. Напишите FН=2 * 108L4Jdi, ФН и=Ф/я / потому что;Ф ‘Ри=Фа тг а;ФН=Ф-Н-cos6i=ФТЛ тг в cos6t;Пай=Р’ Ри sin6i=ФН тг в sin6X. Для колес направление силы противоположно, поэтому RGD= — RP2, RC= — RP\Fn= — Fa i\Fai= — Fr2. Эквивалентный прямой зуб приводит прямые зубчатые конические колеса к цилиндрическим. Профиль зуба скошенного колеса (рис.4.41) очень близок к контуру зуба эквивалентного цилиндрического колеса, а его разделительная окружность получается разверткой дополнительного конуса на плоскости. 130 мм Диаметр треугольни
к ОАО эквивалентного колеса круг отдел G G G e. / Cos Или две. = Де./ cos6j. (4.37)принять dve. =мецв. И де. =mezi, получаем формулу для определения числа зубьев на эквивалентных колесах z0 / =zj / cos6, -, (4.38) Где zi и G2-действительное число зубьев конического колеса, а i (1 и 2) — индекс конического колеса. Расчет конических зубчатых колес ГОСТом пока не регламентирован, но его рекомендуется проводить с упором на приведенную зависимость от цилиндрических зубчатых колес. Это возможно, если коническое прямое зубчатое колесо представлено в виде цилиндрического колеса с диаметром dVi, dVt и эквивалентным числом зубьев zVl и zv». При расчете конического
зубчатого колеса удобно брать среднее сечение зуба с нагрузкой DSR для рассчитанного зуба, поскольку распределение нагрузки вдоль зуба одинаково во всех сечениях по закону треугольника, где вершина совпадает с вершиной тангажного конуса. Расчет прямого конического зубчатого колеса, учитывая экспериментальные данные о том, что грузоподъемность конического зубчатого колеса составляет всего около 0,85 грузоподъемности цилиндрического зубчатого колеса, можно рассчитать эквивалентное цилиндрическое прямое зубчатое колесо. Расчет прямозубой передачи конуса на контактную усталость активной поверхности зуба проверочный расчет. Формула (4.23) в параметрах линейной зубчатой передачи эквивалентной
цилиндрической формы на среднем дополнительном конусе имеет следующий вид 0/7=ZuZ * 0, 8 5^6KhbK hv [°7d- Дано соотношение между тригонометрическими функциями и формулами (4.36) и (4.37)、 COS61=1—— G=; COS6o = 1== — X — — — ; K i+tg2^Va2+1 » F » 2+1 dl>2< / cos6 > 2! d2cos (90° — S2 » o » B=d — = cos8a=Di cos Sa= Шесть.* После подстановки значений d01 и Uj в исходную формулу 131 и простого преобразования получаем формулу тестового расчета стального прямого конического колеса Лето= Ft+1O В Ig, 85dib и Hnrkn[o?/]»(4.39) Где F/ — мощность окружности, Н;bw-ширина кроны, мм;Z/f=1,76 cos
ZM=275 mpa1/2′, KN$и K liv-коэффициент нагрузки (см. таблицу). 4.9 и 4.10). Расчет конструкции. Заменив значение формулы (4.39) на Ft=2-103M2/diW, b=tybtidi, и решив полученную формулу для dt, запишем: d1=^(zh Z^2K fiv Y3l42kya R UM2+1 0.85 FM[OYA R I2l to1Z, 0 8L,® * NR]/ / и 2+1 или d i — (a u o, 8 5f^[0 » p «2′(4.40)где L42-крутящий момент колеса, Н * м; Kd-вспомогательный коэффициент (сталь прямозубых колес Расчет прямых конических зубчатых колес для расчета усталостных испытаний на изгиб. Записывается [формула (4.27)] по аналогии с линейной цилиндрической передачей °F1=Y n o&W^^F^[o F] r, ( 4 4 1 ) 0>-2 = 0>1urg/Y Fl[o>b, где KFv-коэффициент динамическ
ой нагрузки (см. таблицу). 4.11); KF^ — коэффициент неравномерности нагрузки(см. табл.. 4.9); Y F1 и Y F2-коэффициент формы зубьев эквивалентного колеса (определяется по gv1 и zv2 в таблице. 4.14). Расчет конструкции. Это похоже на расчет цилиндрической шестерни[см. формулу (4.28)]среднего модуля зуба t=CT lO3M2KF b Y F УЗИ м ОД’ (4.42) Где K t-вспомогательный коэффициент, а стальные прямые конические колеса принимают CT=1,45;FM=6/f-отношение ширины зубчатой передачи к среднему диаметру делителя- 132metru, принять 1|) m=0, 3…0.6 при условии выполнения условия 1/) y/? =b /
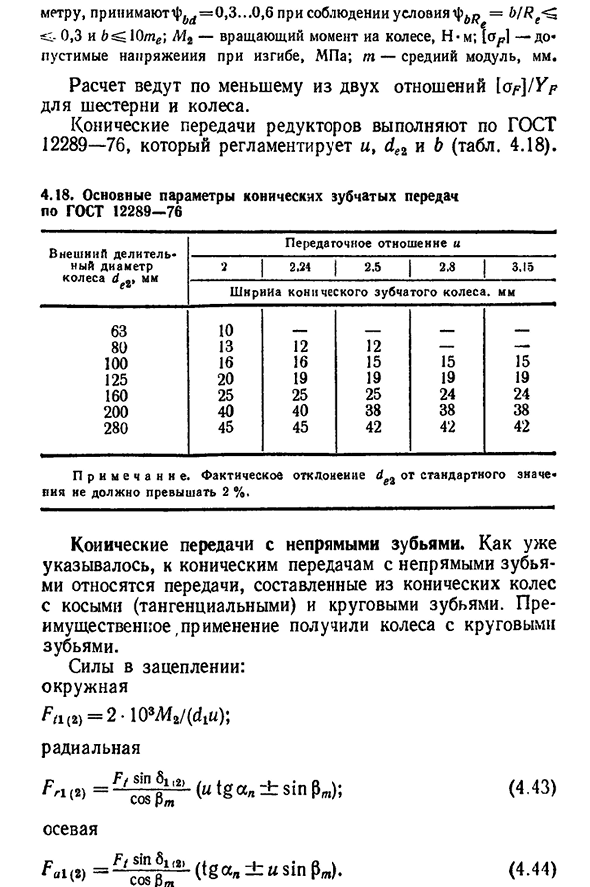
R^<-0,3 и B^L0te; M2-крутящий момент IA колеса, Н-м; [OU?1-up * luscinia давление изгиба, МПа;t-средний модуль, мм. Выполняется ли расчет для меньшего из двух соотношений[o>] / Y/? Для шестерен и колес. Коническая коробка передач выполняет по ГОСТ а, Дей и Б(таблица-тюнинг 12289-76. 4.18). 4.18 основные параметры конических зубчатых колес по ГОСТ12289-76 2.5 2.8 Передаточное отношение и Ширина скоса, мм Диаметр d наружного колеса splitter Шестьдесят три. Десять. Восемьдесят. 13 12 12 — — 100 16 16 15 15 15 15 125 20 19 19 19 19 19 160 25 25 25 24 24 200 40 40 38 38 38 280 45 45 42 42 42 П р и М е ч а н и Е. фактическое отклонение dg3 от стандартного значения не должно превышать 2%. Конические зубчатые колеса с непрямыми зубьями. Как уже упоминалось, конические зубчатые колеса с непрямыми зубьями включают зубчатые колеса, состоящи
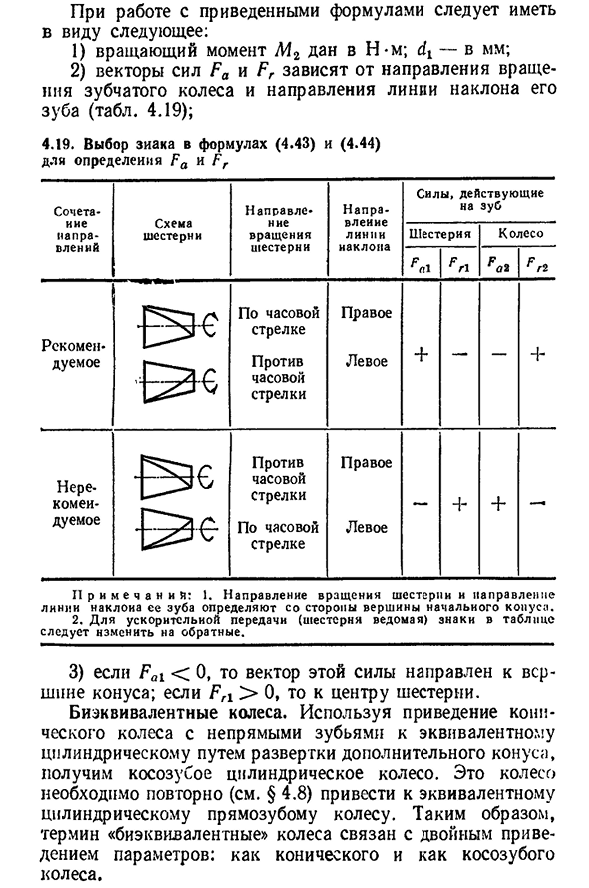
е из конических зубчатых колес с косыми(тангенциальными) и круглыми зубьями. В основном использовались колеса с круглыми зубьями. Мощность передачи: Окружная F a (B)=2-108Afa/(diU); радиальная G Ff sin5i, 2, r l (2)cosφm (u tg a » ±sin pm); (4.43)осевой p_ft sin5i(л «L W cosφct (±u s в tg a» pCT). (4.44) 133. При работе с приведенными выше уравнениями следует иметь в виду следующее: 1) крутящий момент M2 задается Н-м;dt-в мм;2) зависит от направления вращения зубчатого колеса и наклона зубчатой линии 4.19.); 4.19 выберите вход(4.43) и(4.44), чтобы определить Fa и f r Комбинация направлений Зубчатый механизм Направление
вращения шестерни Направление линии наклона Сила, действующая на зубчатое колесо Fal F n FO2F n Рекомендуемый Перевод на E-Pic против часовой стрелки Правильно Левое крыло +—+ Не рекомендуемый Против Часовой Стрелки, По Часовой Стрелке. Правильно Левое крыло — ++ — П р и М е ч а н и я: 1. Направление вращения шестерни и наклонная линия ее зубьев определяются от вершины исходного конуса. 2. Для механизма ускорения(ведомого механизма) табличная метка должна быть обращена вспять. 3)при Fal<0 вектор этой силы направлен к вершине конуса, а при Frl>0-к центру шестерни. Два колеса. Расширяя дополнительный конус, уменьшая коническое колесо с непрямыми зубьями до
эквивалентного цилиндрического цилиндрического колеса, наклонное цилиндрическое колесо это колесо должно быть повторно приведено в движение к эквивалентному цилиндрическому прямому колесу (см.§4.8). Так, термин «завидное» колесо ассоциируется с двойным уменьшением параметров: как коническое, так и косое колесо. В расчетах усталости коническое колесо с тангенциальными и круговыми зубьями представляется в виде биссектрисного колеса с параметром NH o он становится n-по формулам (4.13) и (4.18).* 3. Определите пределы прочности материала колеса,предел контактной прочности (см. таблицу). 4.5) Iim6,=, 8W/? С+ , 5 0 = 18 • 4 7 ,5 4 -1 5 0 = 1000 MPa; Otani N t Y<=2804-70=2.2804-70=630MPa. Предел выносливости на изгиб (см. таблицу 4.7) a F llm6,=8 7 0мпа;°F lim6<=L. 8 C p=l. 8-2 8 0=5 00мпа. 4. Определить допустимые напряжения материала колеса: [a I] z= ( 1 0 0 0 — ° ‘9 5 )/1’2 = 800 МПа; [Ай]4 = (630 •
0,95)/1,2 = 570 МПа. Для расчетного допустимого напряжения возьмем меньшее из значений, полученных по зависимости (4.16): [OYA]=0.45(8004-570)=620 МПа;[OYA]=1.23-570=700 МПА. Допустимое напряжение изгиба [формула (4.17)]для шестерен и колес соответственно 1a=2i / W(m4-1)=0,436. Принимаем Fya=0,4. Согласно таблице. 4,9%=1,05. 6. Дальность передачи[формула (4.24)] 138PO ST COMECON229-75 » a » =125 мм, 7. Нормальный модуль зуба t l=(0,0125… 0.025) Ай-1.56… 3,125 мм. По СТ СЭВ 310-76 составляет ТП=2,5 мм. 8 принять. Определяем по числу зубьев и углу наклона зубьев колеса, определяем заранее заданный угол наклона зуба 0=10°и общее число зубьев z2=(2aw cos0)/ » t » =(2•125 * cos10°) / 2,5 99,/(a-f)-1) = 9 9 /(4 ,5 4 -1 )=
18 и G4=G2-G3=99-18=81 колес. Фактический угол зуба cos0=m » z2/(2aw) = 2,5-99/2- 125 = 0,99; 0 = 8OO6, 35. 9. Проверьте результирующее передаточное число и соответствие заданному. 1/34 = 24/^3 = 81/18 = 4,5. 10. Основные геометрические размеры шестерен и колес. Диаметр делительного круга d3=m «z8 / cos0=2,5 * 18 / cos8°06’35» =45,45 мм; d4=zn » z4 / cos0=2,5 * 81/cos8o06 ’35» =204,55 мм, при этом соблюдается равенство.= 0,5 (^4-/<2) = 0,5 (45,45 4-204,55) = 125 хм. Диаметр окружности вершины da3=d3-j-2m»— 45,454-2-2,5 =50.45 мм; du4=d4 4-2/n » =204,554-2 • 2,5 =209,55 мм, что соответствует предварительно принятому диаметру заготовки. Ширина кроны: колеса 64=f (AAA)=0,4•125=50 мм; шестерни Y3= -(-5 = 5 0 4 -5 = 5 5 хм. Осевой шаг Px=n m n / sm0=3,14-2,5 / sin8°06 ’35″=55,68 мм. Коэффициент осевого перекрытия EP=6A, / Rd; = 62/55,68= 1,1, 11. Скорость угловых окружных
колес nd3n3_3, 14-45, 45-361 с Ygp.——— 611000■= = 0 ‘ 8 6м / с>Согласно таблице. 4.2 примите 8-ю степень точности изготовления зубчатого колеса 12. Определить мощность зацепления:окружность Ft=2-10 «M3 / d3=2-10z. 114/45, 45=5020N; радиальная Fr=(F, tga) / cos0=(5020tg20°) / cos8°06’35″=1840H;ось Fa = Ft tg0w=5020 ‘tg8° ’35″=715H. 13913 берем расчетные коэффициенты: K I=1, 0 9(табл. 4.16); K F a=0.91(табл. 4.16); K I G1=1.01(табл. 4.10); K^=1,0 3 (табл. 4.11); K I p=1,1 9 (табл. 4.9);^=1.42(табл. 4.8). 14. Испытание на усталость контакта: нет.Z/ / Z MZ s[°I];ZH=1.76 cos₽w=1. 76cos8 ° 06 ’35*=1.74; ZM=275Mpa1/®; e»=[1.88-3.2(1/g»3+1 / GM)] cos0=1.65; * o3= * 3/coss8°0S3=18 ° 06’35; GP4 = 64 /
0W»=18.55;/(0,9 5.1,6 5j=0,7 9; Oh= 1,74 — 275 • 0,79 ] / ‘ 1,19 • 1,01 • 1,09 = 640 МПа. Расчетное напряжение превышает допустимое значение[OJ]=620 МПа менее чем на 4%. 15. Трансмиссия ia проверка на усталость при изгибе[формула (4.33) 1. По эквивалентному количеству зубов находим коэффициент формы зуба(см. табл. 4.14); шестерни U^3=4,15; колеса U^4=3,6. Сравнительные характеристики сопротивления усталости при изгибе зубьев: зубчатые колеса[o^s / K^=330/4, 15=198; колесо[o p V K^= = 290/3, 6=80. Из полученных результатов видно, что расчет трансмиссии следует проводить на зубчатой передаче;
Смотрите также:

