Конические сечения

Конические сечения

Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся).

1-й случай. Если секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим 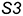(фронталь-но-проецирующая плоскость 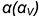, рис. 7.11).

2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность по окружности (горизонтальная плоскость 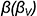рис. 7.11).

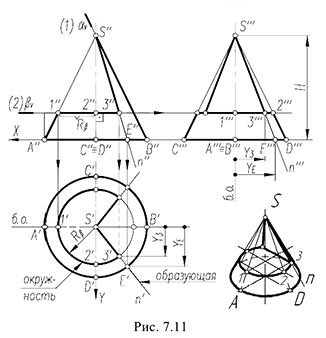
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 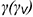параллельна одной образующей рис. 7.12).

4-й случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 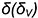параллельна двум образующим и , рис. 7.13).

5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость 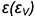, рис. 7.14).

Рассмотрим построение на проекциях конуса линий пересечения для всех пяти случаев сечений. 1-й и 2-й случаи. На рис. 7.11 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью 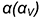, проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью 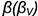, расположенной перпендикулярно оси конуса (2-й случай).

Плоскость 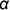пересекает поверхность конуса по образующим , горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки 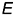, лежащей на основании конуса.

Плоскость 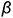пересекает поверхность конуса по окружности радиуса 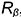, ограниченной линией 3-3 пересечения плоскостей выреза.

Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.

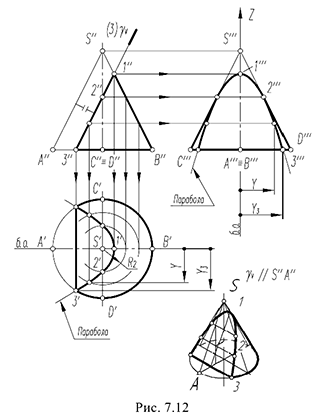
3-й случай. На рис. 7.12 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 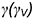, расположенной параллельно одной образующей конуса .

Плоскость 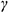пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена).

Построение проекций этих точек выполнено по их принадлежности: -точка 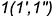— лежит на проекциях характерной образующей

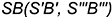
-точки 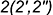— лежат на проекциях характерных образующих 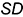и 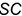, горизонтальные проекции которых построены с помощью параллели радиусом 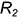(алгоритм I);

-точки 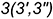— лежат на окружности основания конуса: горизонтальные проекции этих точек определяются по линии связи на горизонтальной проекции окружности основания, а их профильные проекции построены по координате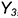

• проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате ).

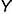Оформление очерков проекций видно из чертежа.

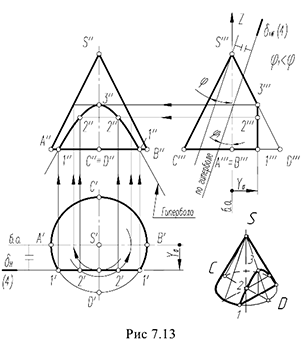
4-й случай. На рис. 7.13 показано построение проекций конуса со срезом фронтальной плоскостью 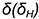, расположенной параллельно двум образующим конуса и .

Плоскость 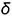пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза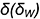

Оформление очерков проекций видно из чертежа

На рис. 7.13 на профильной проекции конуса показано положение секущей плоскости 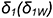под углом 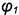к оси конуса. При 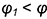плоскость пересекает поверхность конуса также по гиперболе.

5-й случай. На рис. 7.14 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 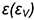, пересекающей все образующие конуса под углом 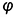к оси, отличным от прямого.

Плоскость 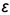пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 я промежуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Точки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции по координате 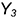(алгоритм 1).

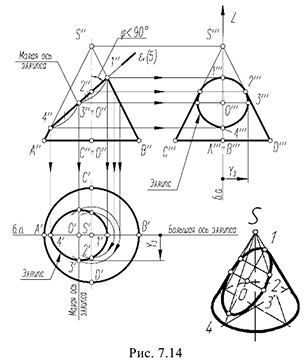
Оформление очерков проекций видно из чертежа. !!! Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.

Построение проекций прямого конуса со срезами плоскостями частного положения

На рис. 7.15 показан пример построения проекций прямого кругового конуса со срезами фронтально-проецирующей плоскостью 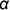и профильной плоскостью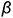

Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.

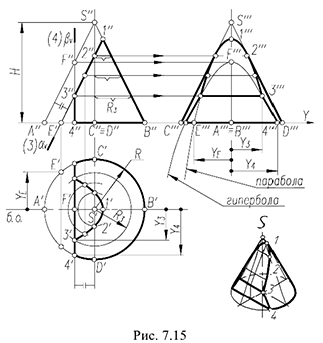
Графический алгоритм: 1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания 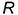и высоте 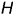фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью 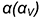и профильной плоскостью 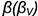. 2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выполнить графический анализ сечений.

2.7. Фронтально-проецирующая плоскость 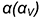параллельна одной образующей конуса 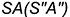и пересекает его поверхность по участку параболы 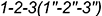, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 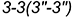плоскостей срезов 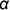и .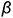

2.2. Профильная плоскость 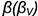параллельна двум образующим конуса 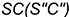и 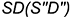и пересекает его поверхность по участку гиперболы 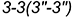, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 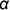и 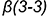и плоскости 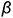с основанием конуса (4-4).

3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:

3.1. Плоскость среза а определяет видимая горизонтальная проекция участка параболы 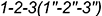, построенной по горизонтальным проекциям обозначенных точек:

-точка 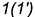лежит на образующей ;

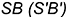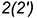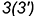-точки и построены по принадлежности соответствующим параллелям (алгоритм I).

3.2. Плоскость среза 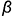определяет вертикальный видимый отрезок 4′-4′ вырожденной в линию проекции профильной плоскости, точки 4(4′) которой лежат на очерковой окружности основания конуса.

!!! Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).

4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура.

4.1. Горизонтальный очерк определяют участок окружности и отрезок .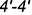

4.2. Внутренний контур определяет видимый участок параболы .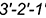

5-е действие. Достроить профильную проекцию конуса со срезами, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов.

5.1. Плоскость среза а определяет видимый участок параболы 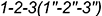, построенный по профильным проекциям обозначенных точек:

• точка 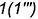— лежит на характерной образующей ,

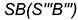-точки 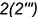— лежат соответственно на характерных образующих 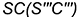и ;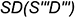

• точки 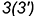— построены по координате .

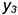5.2. Плоскость среза 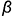определяют видимые участки гиперболы 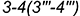, ограниченные видимым отрезком 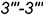(построен) и видимым отрезком 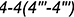, точки которого построены по координате .

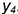6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.

6.1. Профильный очерк определяют:

• слева — участок 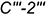образующей ;
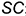• справа — участок 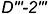образующей ;
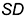• сверху — участок параболы ;
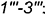• снизу — проекция основания конуса.

6.2. Внутренний контур определяют:

• видимые участки параболы
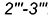
• видимый отрезок 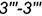пересечения плоскостей срезов 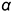и ;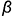
• видимые участки гиперболы .

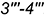7-е действие. Оформить чертеж конуса выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

 Начертательная геометрия для 1 курса

Возможно эти страницы вам будут полезны:

Геометрические тела — цилиндр конус

Коническая поверхность вращения — прямой круговой конус

Торовая поверхность — тор

Сферическая поверхность — шар