Оглавление:



Конденсатор в цепи синусоидального тока
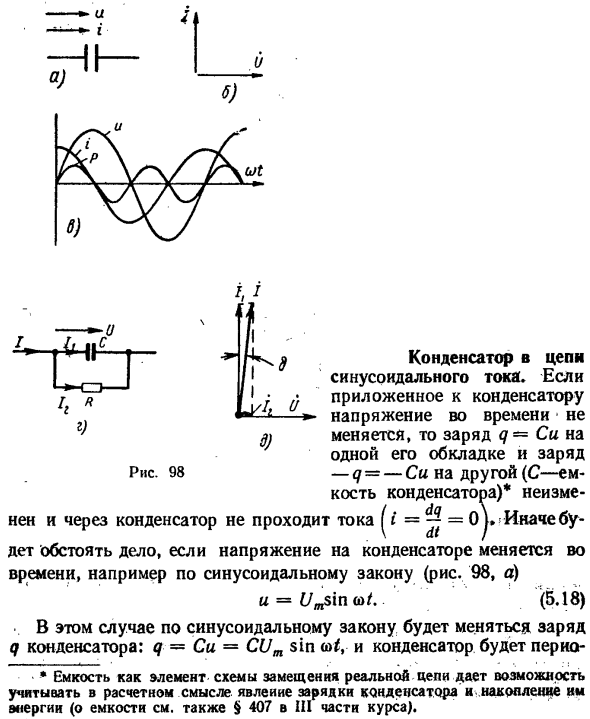
Конденсатор в синусоидальной цепи тока. Если напряжение, приложенное к конденсатору, не изменяется с течением времени, заряд q = Cu одной пластины и заряд q = Cu другой (C-емкость конденсатора)*не изменяется, и ток не проходит через конденсатор, иначе ситуация будет иной.
- Если напряжение на конденсаторе изменяется со временем, например по синусоидальному закону (рис. 98, а) В этом случае, согласно закону синусоиды, заряд Q конденсатора изменяется следующим образом: q = Cu = CUm sinw/,
конденсатор периодически перезаряжается. Людмила Фирмаль
Когда конденсатор периодически перезаряжается, зарядный ток течет к конденсатору. Положительное направление тока, протекающего через конденсатор в цепи к?? 98, и это совпадает с положительным направлением напряжения, и сравнение между (5.18) и(5.18′) показывает, что ток, протекающий через конденсатор, превышает напряжение на конденсаторе на 90°.
Таким образом, на векторной диаграмме, рис.98, вектор тока b/вектор напряжения 90°впереди. Амплитуда тока 1Т равна амплитуде напряжения Полностью разделить с емкостным ХС (5.19)) Конечно. * ’ ■ / Т = «>укус — Емкость обратно пропорциональна частоте и измеряется в Омах. график мгновенных значений u, i и p показан на рисунке. 98, С. мгновенная мощность pssui = * ~~ грех 2пк /. В Q1 периода конденсаторы потребляют энергию от источника питания.
- Эта энергия используется для создания электрического поля в capacitor. In во 2-й четверти периода напряжение на конденсаторе уменьшается от максимального до нуля, и энергия, накопленная в электрическом поле, отдается источнику (мгновенная мощность отрицательна). в 3-й четверти периода энергия накапливается снова, а в 4-й четверти энергия отбрасывается.
При интеграции обеих сторон равенства с течением времени Мы получаем И = ■ 1 J idt. (5.20 утра)) Уравнение (5.20) позволяет определить напряжение конденсатора через ток конденсатора. При постановке задачи о синусоидальном токе, протекающем через конденсатор, предполагалось, что
диэлектрик, разделяющий пластину конденсатора, будет идеальным диэлектриком без потерь энергии. Людмила Фирмаль
Однако, когда синусоидальное напряжение прикладывается к пластику конденсатора, разделенного твердым или жидким диэлектриком, последний всегда имеет некоторую потерю отвода. Эти потери относительно невелики и часто могут быть проигнорированы.
Если вы хотите учесть их в расчетах, то конденсаторы заменяются расчетной схемой замещения, показанной на рисунке. 98, g. In в этой схеме активный резистор f соединен параллельно с емкостью C, потери энергии которой имитируют потери энергии фактического диэлектрика. ГОК 7 через конденсатор равен геометрической сумме 2 токов: ток I>через емкость, которая на 90°опережает напряжение (/конденсатор (рис. 98, е), и активное сопротивление, которое относительно мало по величине/фазе соответствует U).
Поэтому ток через конденсатор с неидеальным диэлектриком проходит только под углом чуть меньше 90°и опережает напряжение. Ток 6 / текущий угол 6 обычно называют потерей angle. It зависит от типа и частоты диэлектрика, в лучшем случае несколько секунд, а в худшем-несколько градусов. величина tgd описана в таблице (см. стр. 717), которая характеризует характеристики различных твердых и жидких диэлектриков.
Смотрите также:
| Синусоидальный ток в активном сопротивлении. | Умножение вектора на J и на — J. |
| Индуктивность в цепи синусоидального тока. | Основы символического метода расчета цепей синусоидального тока. |

