Оглавление:






Конденсация на поверхности вертикальных труб
- В 1916 году Нуссельт предложил теоретическую зависимость среднего коэффициента теплоотдачи чистого насыщенного пара, который конденсируется на поверхности вертикального и горизонтального. В обоих случаях предполагалось, что движение жидкости является полностью вязким, что трение на границе раздела между паром и жидкостью невелико и что отношение силы инерции при движении жидкости вниз пренебрежимо мало. С тех пор было показано, что последние 2 предположения обычно оправдываются, но во многих случаях движение жидкости является турбулентным. Это обычно происходит при конденсации на длинной вертикали.
В верхней части трубы движение конденсатной мембраны ламинарно, и когда опа достигает определенной толщины, движение становится турбулентным, и уравнение Нуссельта становится неприступным. Критерием перехода от одного вида упражнений к другому является величина Рейнольдса number-Be. In в случае толщины пленки xb, согласно обычному определению, движущейся вниз по вертикальной трубе диаметра d со средней скоростью u>гидравлического радиуса, мы обнаружили, что это просто xe.
Что касается величины поверхности нагрева, то перекрестный ток занимает среднее положение. Людмила Фирмаль
Поэтому для расстояния b от вершины трубы, где толщина пленки равна xe、 Ке = — ПГ ^ — (27.6) Массовый расход равен hei ^ nP, а массовый расход на единицу периметра трубы равен hey$.Это значение, обозначаемое буквой G, увеличивается от нуля в верхней части трубы до максимума в нижней. Если вы присвоите ему номер Рейнольдса、 БЖ = ^. (27.7) Ламинарный поток присутствует, когда число Рейнольдса меньше 2000, а турбулентный поток превышает-2000.Это ограничение применимости уравнения уравнения.
Поскольку диаметр трубы значительно больше толщины пленки, цилиндрическую систему координат можно представить почти в виде прямоугольника. Начало координат находится в верхней части трубы, ось x перпендикулярна поверхности трубы, а ось y перпендикулярна вниз. Следующее уравнение Навье-Стокса (I. 53) является основой для гидродинамического анализа. Это всегда предшествует анализу теплопередачи. Когда вы устанавливаете движение, левая часть уравнения равна нулю.
Завиток и они будут равны IG и нулю. Доктор справа Поскольку нули частей равны, а изменения как по оси y, так и по оси z игнорируются, формула(11. 53) принимает вид: Риу _ __ В ’(27.8)) поскольку ось Y является вертикальной, масса сила Y является упрощенной. Таким образом, уравнение(27.8) принимает вид: _____ ДХ * в (27.9)) Формула (27. 9) интегрируется 2 раза и выглядит так: 2 произвольные константы определяются наложением 2 граничных условий. Последнее условие эффективно, когда трение на границе раздела пара и жидкости незначительно. При применении этих значений、 ^ = ^-(^-4). (27.11) Массовый расход можно найти, интегрируя всю толщину пленки.
Если мы проигнорируем увеличение границы с увеличением x、 О. О (27L2) Отсюда массовый расход на единицу трубы, указанный в G, выглядит следующим образом: Р.^ = (27.13) Чтобы определить средний коэффициент теплопередачи, используйте уравнение теплового потока для бесконечно малого отрезка трубы, yu, на расстоянии y от вершины. ЛД-Али-Лу -*.). (27.14) поскольку температурный градиент по оси Y считается незначительным, вся теплота конденсации, выделяемая на границе раздела пара и жидкости, передается горизонтально путем теплопередачи на поверхность трубы.
- Если толщина пленки равна x9, ее можно записать Х9 . Уравнение (27.14) и (27.15) в совокупности、 (27.15)) (27.16)) По определению, локальный коэффициент теплопередачи равен s1c _ _ _ _ г. Где cig-минимальная скорость конденсации в кг / ч, а g-скрытая теплота испарения.
Раздел однако, локальная скорость конденсации может быть выражена Следующим образом: AG / t 4 04 la-yaBlu-lu * Уравнение (27.16) — из(27.18): a _ g LU К (ш-18 Лу (27.19) Или Хег ЛГ х ю (27.20 )) Для всей длины а трубы, в которой присутствует ламинарное движение пленки, это выглядит так: Откуда Подробнее-РТ Великобритания А-Ата-Ате」 (27.21) (27.22) Подставляя формулу (27.20) в значение 18P-19, получаем: Из Формулы (27.13) следует, что толщина пленки равна Этот результат присваивается выражению (27.23).■ «- М ^(€) Т ^ Л^’ (27.23) (27.24) (27.25 )) Выражение (27.25) интегрируется в диапазоне от y = 0 до y = b и от G = 0 до G = Gb.
Таким образом, при противотоке можно применять наименьшую поверхность нагрева для данного количества передаваемого тепла и при данных начальном и конечном температурных напорах. Людмила Фирмаль
После преобразования получаем формулу для среднего коэффициента теплоотдачи в ламинарной области. Теннесси= (27.26) При преобразовании уравнения (27.22) значение представляется в виде: Вы можете. г (27.27) Если вы присвоите выражение (27.27) выражению (27.26), вы получите: ОЖ. Если обе части формулы (27.28) являются кубиками, решенными относительно ам, и извлекается 4-й маршрут, то можно легко получить средний коэффициент теплопередачи.
Средний коэффициент теплопередачи также может быть определен по формуле (27.7). для этого преобразуем уравнение (27.26) в следующий вид: ам (Д — = М7(^)3 = 1.47 (Вег) » 5-.(27.30) Это число Рейнольдса в нижней части области ламинарного движения потока в щели вдоль трубы. Формула (27.29)показывает зависимость ам от разности температур конденсатной пленки. Когда конденсатор работает, охлаждающая жидкость, протекающая по трубе, повышает температуру. Поэтому предположение о том, что-1B является постоянным, не соблюдается. Однако, зависит только от степени перепада температур по оси Y, таким образом, изменение в ам по этой причине, как правило, небольшие.
Физические свойства конденсата изменяются в зависимости от температуры, но существенно изменяются только свойства вязкости. Вязкость определяется по температуре насыщенного пара-y(^ P-при этой температуре могут быть получены и другие свойства. Общий тепловой поток фактически является суммой скрытой теплоты конденсации, поэтому скрытая теплота конденсации также может быть немного изменена. Тепло выделяется при переохлаждении жидкости в конденсате film. it принято умножать r на коэффициент^ 1 Выражение (27.29) заменить на g. Формула (27.29)была сопоставлена с экспериментальными данными и оказалась заниженной.
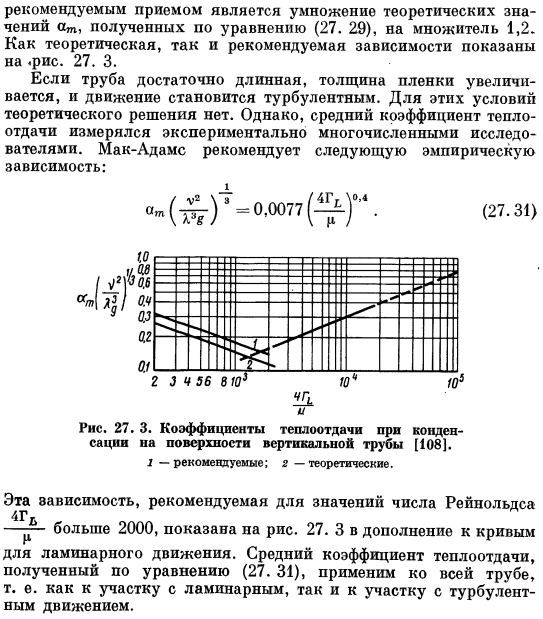
Предполагается, что волна на поверхности конденсатной пленки вызывает некоторое перемешивание. экспериментальное значение Ам находится в диапазоне выше расчетного значения по формуле (27.29), а в некоторых случаях даже на 50%.Таким образом, рекомендуемый метод заключается в использовании формулы(27. 29) заключается в умножении теоретического значения от полученного на коэффициент 1,2.Теоретические и рекомендуемые зависимости показаны на рис. 27.3. Если труба достаточно длинная, то толщина пленки увеличится и движение будет нарушено. Теоретического решения для этих условий не существует. Однако средний коэффициент теплопередачи был измерен экспериментально многими исследователями.
Мак Адамс рекомендует следующие эмпирические зависимости: (27.31) 27. 3.Коэффициент теплопередачи при конденсации на поверхности вертикальной трубы[108]. 1-рекомендуемая; 2-теоретическая. Эта зависимость рекомендуется для числа Рейнольдса 4Gd — — — Более 2000 показано на рисунке. 27. 3 в дополнение к кривой ламинарного движения.
Смотрите также:
| Максимальный тепловой поток. Плёночное кипение | Конденсация на горизонтальных трубах |
| Конденсация. Механизм конденсации | Перегретый пар. Влияние неконденсирующихся газов |

