Конденсация

Конденсация

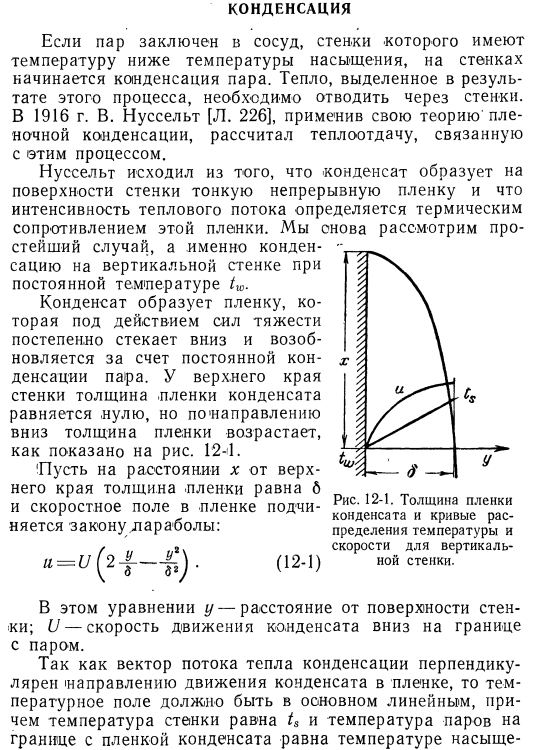
• Если пар герметизирован в контейнере, где температура стенок ниже температуры насыщения, начинается конденсация пара на стенках. Тепло, выделяющееся в результате этого процесса, должно быть удалено через стену. В 1916 Году В. Нусерт. [226], используя теорию пленочной конденсации, он рассчитал соответствующий теплообмен Рисунок 12-1. Толщина конденсационной пленки и кривая распределения температуры и скорости вертикальной стенки. В этом процессе.

Нуссельт исходил из того, что конденсат образует на стенках тонкую сплошную пленку, а интенсивность теплового потока определяется тепловым сопротивлением этой мембраны. Здесь тоже рассмотрим простейший случай-конденсацию на вертикальной стенке при постоянной температуре tw. Конденсат образует пленку, которая под действием силы тяжести постепенно стекает вниз и возобновляется, из-за чего пар постоянно condenses. At у верхнего края стенки толщина равна нулю, а толщина уменьшается, как показано на рисунке 5. 12-1.

Если для системы известны её термическое и калорическое уравнения состояния, то тем самым задано полное термодинамическое описание системы и можно вычислить все её термодинамические свойства. Людмила Фирмаль

«Предположим, что на расстоянии x от верхнего края толщина пленки равна q, а поле скоростей пленки подчиняется закону параболы. Сконденсированной пленки, но увеличенной в направлении пленки、 (12-1） В этом уравнении y-расстояние от стены. U-скорость конденсации вниз на границе с паром. Поскольку вектор теплового потока конденсации перпендикулярен направлению движения конденсата в пленке, температурное поле практически линейно, температура пара на границе между температурой стенки tₛ и пленкой конденсата является температурой. Niya. It может показаться удивительным, что температурное поле в этом случае имеет иную форму, чем пограничный слой жидкости или газа (см. § 6-4).

Это объясняется тем, что в ранее изученной задаче все тепло, передаваемое стенкам, происходит внутри пограничного слоя, но в этом случае за счет конденсации пара все тепло выделяется на внешней поверхности пленки жидкости. Исходя из вышеизложенного, тепло, передаваемое через конденсированный мембранный элемент высотой dx и 1 измерения в горизонтальном направлении вдоль стенки, определяется по следующему уравнению: йд = л-ДХ (tₛ-ТВт). (12-2） Коэффициент теплопередачи a можно снова определить из уравнения.  йд = adx (по tₛ-ТДж.

Отсюда Скорость, с которой конденсат течет через печь, может быть рассчитана с использованием уравнений равновесия рассматриваемых элементов. Вес элемента должен уравновешиваться напряжением трения t на поверхности пластины. Gp3dx =xdx. Силы ускорения и давления игнорируются как несущественные. Используйте уравнение Ньютона (6-2) для выражения напряжения трения, решите уравнение для градиента скорости на стенке и получите следующее: (ду _2u■в gp3 — ды) Ж-1 т ’ Откуда? (7 = ^-8′. 2р. — Таким образом, выражение (12-1) изменяется на следующий вид: «= — ts, (2+ — £）.

Средняя скорость секции x um составляет 2 / ₃maxi Кривая скорости a распределения параболы： „М = < ⁸ *- (12-4） Конденсат следующей массы проходит через сечение х. G = p “ ₘ⁸-f⁸»> Через поперечное сечение на расстоянии dx в направлении движения конденсата, жидкость проходит только ДГ = ^ 8m8. (12-5） Это увеличение происходит за счет конденсации пара. Если подставить значение dq = ifgdgy в Формулу (12-2), то ifg-это скрытая теплота испарения на единицу массы жидкости. ДГ = — ± — ДХ (Т-tₐ) (12-6） Фе И если мы уравняем правую часть уравнения (12-5) и  (12-6), то получим уравнение. Dxifₛg? Т [ы] .

Путем интеграции、 Ил — _ т} х Если коэффициент вязкости заменить на коэффициент кинематической вязкости v, то для толщины пленки состояния получается следующая формула: Конденсатор. ^ Х  (tₛ_fw) х Кроме того, коэффициент теплопередачи выглядит следующим образом: «В» В виде критерия он имеет вид: (12-7） (12-8） (12-9） 4А（^-М） Решение (12-8) обеспечивает локальное значение коэффициента Теплопередающая лента на расстоянии х от верхнего края печи. Среднее значение коэффициентов для всего расстояния определяется по формуле а =7₃a. (12-10） Согласно формуле (12-9), значение критерия Нусельта зависит от безразмерной величины в правой части уравнения. Это число иногда называют критерием Шервуда.

Физические параметры формулы связаны с конденсатом. Когда толщина конденсированной пленки достигает определенного значения, кинетический режим становится турбулентным. Теплопередача через турбулентную конденсированную пленку может быть рассчитана методом, связанным с турбулентностью жидкости или газа вдоль пластины. Такой расчет осуществляется с помощью w.  grigule [l. 227]. Результаты расчетов показывают, что для турбулентных конденсированных пленок критерий нуссельта является функцией безразмерного значения уравнения (12-9) и критерия Прандтля конденсата.

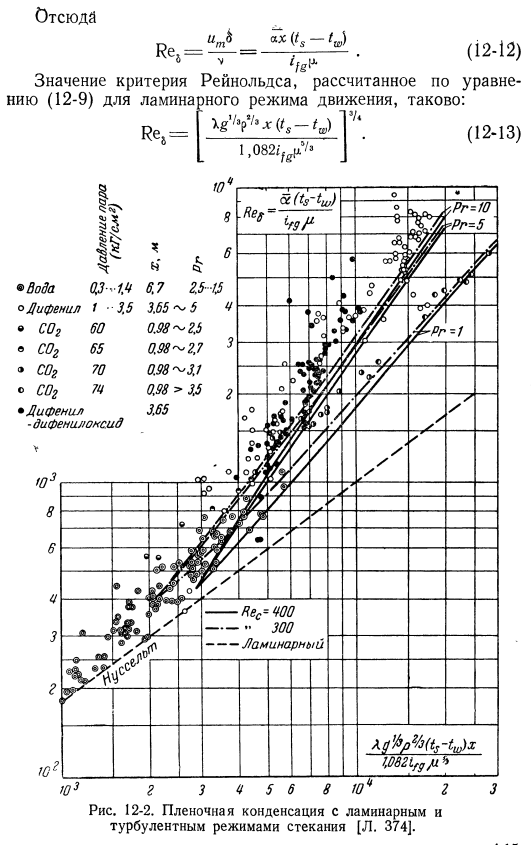
• Уравнение теплопередачи для турбулентных конденсированных пленок очень сложное. Поэтому удобнее использовать значение коэффициента теплопередачи, которое показано на рисунке. 12-2. In на этом рисунке значение критерия Рейнольдса для конденсированной пленки строится как функция безразмерной величины Критериями пракдтл считаются параметры. Значение критерия Рейнольдса является толщина мембраны конденсатора 6 и средняя конденсации курс единой системы обмена сообщениями re₄=! ^ (12-11） Среднее значение коэффициента теплоотдачи рассчитывают исходя из того, что тепло, поступающее в стенку по всей длине x, образуется за счет выделения конденсатом скрытой теплоты конденсации, проходящей через поперечное сечение пленки в точке x. » (<₅- u=₽vfg⁸ ’ Отсюда uₘbah (tₛ-м .

Вы можете сделать следующее: = — о Значения критерия Рейнольдса, рассчитанные по ИЗОСЛОЕВОМУ режиму движения, выглядят следующим образом: «Ля. «/«. 4/4 ’7 ^ (12-12） (12-9) ） Ре= & ： (12-13） ■ byshot 8. О Хм. .Дифенил-родственный DDA 9 .Да .•Дифенил дифенил сульфид 1, 082 .7 //> Кес = Чу * * 300 Дамнан !Соosосоogсог .Ч, ч, ч .ОД-1, 4 1-3 .5 60 .65 .70 .74 .3 .65 5 0 .98 ^ 2 .5 0 .98 2 .7 098 ^ 3 .1 0 .98> 3 .5 3 .65 .Agftpfyts-tuJz7, 082tf₉p* ⁴2 Рисунок 12-2 .Ламинарный поток и Турбулентный режим оттока[л . 374] .3 .Эта зависимость показана на рисунке .12-2 ломаная линия .Режим турбулентности характеризуется пучком из 2 линий на рисунке .12-2 .1 из них относится к критическому значению критерия Рейнольдса перехода к турбулентному Rec = 400, еще 1 относится к переходу к Rec = 300 .

Для каждой конкретной термодинамической системы её уравнения состояния устанавливают по экспериментальным данным или находят методами статистической физики, и в рамках термодинамики они считаются заданными при определении системы. Людмила Фирмаль

Сравнивая взаимное расположение линий и точек, можно сделать вывод, что расчетные данные Rec = 300 хорошо согласуются с reality .In область ламинарного движения, теория нуссельта подкреплена опытом .Нуссельт также рассчитал теплопередачу при конденсации в горизонтальной кольцевой трубе .Результаты этих расчетов можно свести к следующему: среднее значение коэффициента теплопередачи горизонтальной трубы диаметром d равно среднему значению коэффициента теплопередачи вертикальной стенки на высоте x = 2, 5 D .Если сверху и снизу расположено несколько горизонтальных труб, то конденсат будет перетекать из верхней трубы в нижнюю .one .As в результате этого теплопередача каждой последующей трубы (рис .12-3) уменьшается .

По расчетам Нуссельта, во 2-й трубе тепловой поток составляет всего 60% от теплового потока первой трубы .Такое снижение теплопередачи можно значительно уменьшить, применив расположение труб по схеме J’inabo (рис .12-4) .Справедливость теории пленочной конденсации нуссельта подтверждается многими экспериментами .Однако в некоторых случаях могут быть получены более высокие экспериментальные данные .E . Schmidt, V .Schurig>и V .Cell shop[L . A .228]указывают на то, что это связано с тем, что конденсат не всегда образует сплошную пленку, а пар иногда конденсируется в виде мелких капелек, постепенно увеличиваясь, а затем стекает вниз, собирая капли всего конденсата вдоль поверхности .way .In в этих местах сразу же появятся новые мелкие капельки .

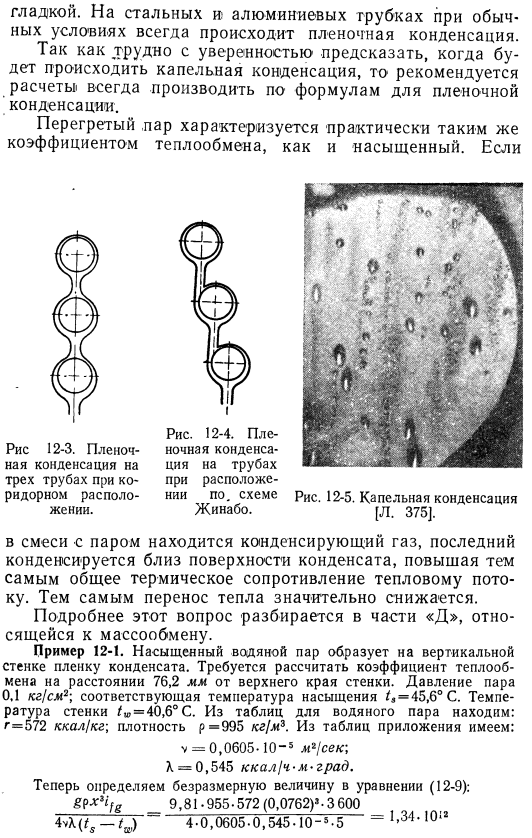
Рисунок 12-5 показывает этот тип капельницы condensation .It понятно, что теплопередача при капельной конденсации выше, чем в случае пленочной конденсации .В США было проведено множество экспериментов по выявлению условий, присущих конденсации пленок и капель .Чистый пар на чистой поверхности всегда образует пленку конденсата .Примеси и поверхностные загрязнения в паре способствуют образованию капель при конденсации .Особенно это касается жирных кислот .Образование капель происходит чаще на шероховатой поверхности Smooth .In стальные и алюминиевые трубки, в нормальных условиях, конденсация фильма всегда происходят .

Трудно достоверно предсказать, когда произойдет конденсация, поэтому рекомендуется провести расчеты !Пленку всегда производят по конденсирующей формуле .Перегретый пар характеризуется коэффициентом теплопередачи, примерно таким же, как и насыщение .Если .. Я. .Рисунок 12-3 .3 .конденсация пленки трубы в расположении прохода .Я .. Рисунок 12-4. Пленочный конденсат на трубе при размещении по схеме jinabo. Рисунок 12-5. Капельная конденсация[л.  375]. Сконденсированный газ смешивается с паром, последний конденсируется вблизи поверхности конденсата, тем самым повышая общее тепловое сопротивление тепловому потоку. Таким образом, теплопередача значительно снижается.

Этот вопрос будет рассмотрен более подробно в части «d», касающейся массопереноса. Пример 12-1. Насыщенный водяной пар образует конденсированную пленку на вертикали wall. It необходимо рассчитать коэффициент теплопередачи на расстоянии 76, 2 л от верхнего края стенки. Давление пара 0, 1 кг}см2 соответствующая температура насыщения / i = 45, 6 ° c температура стенки / w = 40, 6°c из таблицы водяного пара, g = 572 ккал) кг плотность p = 995 кг / и 3 известны. Из таблицы приложений： в =0, 0605-10-⁵m ^ сек Х = 0, 545 ккал! Х-м-привет.

Здесь мы определяем безразмерную величину по формуле (12-9). _ 9. 81 «955-572（0. 0762） ’-3 600 4vx (^_/ₐ) — 4-0, 0605. 0, 545. Значения i0 » с-5-в34-101′ Критерии нуссельта*. Ну = ^ 1. 34-1О ’ » = 1. 08-10 *. Отсюда определяется локальное значение коэффициента теплоотдачи 0 545 а= q762 «’ 1, 08-103= = 7⁷⁴⁰kcal! М2-ч-град И высота в среднем 76, 2 мм： а = 4 / 3-7 740 = 10 300 ккал! М2-Ч’град. Средний коэффициент теплопередачи для горизонтальной трубы диаметром d = 30, 4 мм будет таким же. Это свидетельствует о том, что значение коэффициента теплопередачи в момент конденсации очень велико.

Смотрите также:

• Предмет теплотехника

Свободная конвекция в жидкости, заключенной между двумя плоскими стенками	Испарение
Смешанная свободная и вынужденная конвекция	Тепловое излучение