Оглавление:
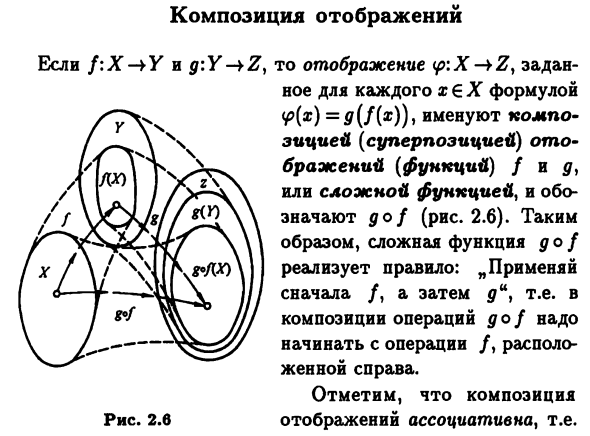

Композиция отображений
- /: «-> Еe g: Если Y-> Z, отобразить (p: X-tZy Указано в х и х выражениях (P (x) = Y, g: Y- + Z ч ч: Когда Z-> H, (боров) = Сжо (гоф). Это можно описать проще как червяк. Для того, чтобы убедиться, Это так. = h ((gof) (x)) = h (g (f (x))). Отображение 1x ‘• определено для любого множества X X- + X, называется идентичным и часто указывается Также задается idx и формулой Ix (x) = x YeeX. его -Действие — оставить все Местоположение.
Следовательно, если f ~ l — биективная обратная биекция /: A «-4U, затем f» lof-Ix <, a / o / ~ 1 = / y, где 1x и / y Отображение идентификатора для набора X и Y соответственно. И наоборот, отображение f: X- ¥ YEg: Y- * X Если это gof = Ix и f0 e = fy, функция / биективна. g-обратная биекция. Очевидно, что если / биективно X на Y, g биекция Y на Z, а gof Биекция X к Z, и f ~ log ~ l обращены Биективные.
Смотрите также:
| Сюръекция, инъекция и биекция | Произведение множеств. График отображения |
| Сюръекция, инъекция и биекция | Упорядоченные множества. Элементы комбинаторики |

