Оглавление:




Компоненты векторов и тензоров в криволинейных координатах
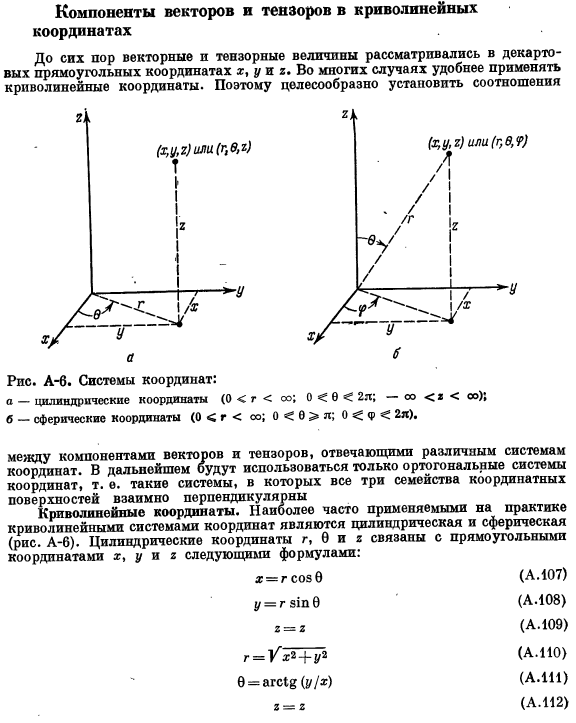
- Ранее, вектора и величины тензора были рассмотрены в декартовы Декартовы Декартовы X и Y, и X. Это часто более удобным в использовании криволинейных координат. Так… Рекомендуется установить соотношение. Рисунок А-6. Система координат: a-цилиндрические координаты Б-сферические координаты. Между векторами и тензорами компоненты, соответствующие различным координатам systems. In в дальнейшем используется только прямоугольная система координат. То есть такая система Все 3 семейства координатной плоскости взаимно перпендикулярны. Криволинейные координаты. Наиболее часто используемые криволинейные системы координат на практике являются цилиндрической и сферической рис.
Цилиндрические координаты r, 0 и x ассоциируется с Декартовыми координатами x, y и x, используя следующую формулу: Элемент дуги пространственной кривой, yz, представлен приращением цилиндрических координат Определена связь между Декартовыми координатами и сферическими координатами По формуле: X =Г81П0сО5ф (а.114) у=гз1п051пф (а.115) г=гсоз0 (а.116) г= 4 — / х24-у24-г2(А.117) 0×18 ^ х2+!г( А. 118.) Для элемента дуги УГ, выражение Dx, dz, dx, yes, d показывает множество криволинейных координат, соответствующих 2 произвольным ортогональным системам.
Если составляющую гравитационного ускорения в направлении х обозначить через то дифференциальное уравнение пограничного слоя (6-16), включая член гравитационного ускорения для стационарного потока, будет иметь вид: Уравнение Навье-Стокса для направления, перпендикулярного поверхности, в результате анализа порядка величин упрощается: др указывая на то, что в этом случае давление на нормалях к поверхности непостоянно. Людмила Фирмаль
Эти 2 комплекта взаимосвязаны Отношения, которые могут быть описаны в общих чертах как: Рисунок А-7.Разложим вектор V на компоненты прямоугольной и цилиндрической систем координат. Масштабный коэффициент A / and(также называемый коэффициентом хромоты), в частности, является функцией пространственных координат (A. 113)и (A. 120). Преобразование векторных компонент. На рисунке А-7 показан вектор I、 Разложены на составляющие, проекция которых отображается на соответствующие оси прямоугольной и цилиндрической системы координат. Основные расчеты на основе тригонометрии Следующая формула, устанавливающая корреляцию между проекциями векторов этих систем, ориентируется на соотношение.
- Аналогичное уравнение может быть получено для проекции сферической системы координат. В общем случае связь между компонентами вектора o кривой системы d2> dz и 01″0a» 0z, которые взаимно ортогональны, описывается следующим образом: Коэффициент пропорциональности 1 {, {уравнение (A. 136) и (A. 137)) называется Косинусом orientation. In фактически, каждый коэффициент является Косинусом угла. Направление формируется единичным вектором Γ и единичным вектором 4 в направлении. Косинус направления удовлетворяет следующим соотношениям: Далее, коэффициент f h — это коэффициент хромоты A /и Формула Читатель найдет общую формулу(А. 136)-(А.
Можно быть уверенным в точности » ортогональной системы координат, в частности Пример прямоугольного ПАЙ’Н ^ Лмпгч » Овноптор1е Рубшоптопределтю; что называется совместимостью 3 таких величин, причем при переходе от одной системы координат к другой Отношения между Компонент тензора 2-го Диа-м, / соответствующий кривой системы координат dxd2″dz и dx, d2″ d3 описывается следующим образом: Эти выражения на самом деле являются определением 2-го тензора pa ^ ha. Аналогично, выражение может быть представлено для более высокого тензора звона.
Это означает, что там пренебрегли влиянием объемных сил внутри жидкости, Однако в условиях естественной конвекции движение жидкости 26—308 401 вызывается исключительно действием объемных сил. Людмила Фирмаль
Пример А-3.Закон трансформации Вектор и тензорное произведение-запишите соответствующее правило преобразования при переходе от одной системы координат к другой, указав, что произведение[oX u]является вектором. Произведение (o; t) является скалярным. Решение. Мы это выясним: Формула(А. 143) отношения (А. 137) и тот же формат. Это означает, что компонент произведения[I X u]преобразуется как компонент вектора. При выводе формулы(А. 143) использовалась формула (A. 139). Отношения (А. 143), условия(А. 138).Окончательная формула (A. 144)имеет точно такую же форму, как и исходная формула, написанная в верхнем ряду、 Сумма (o; t) равна a scalar.
Смотрите также:
| Тензоры второго ранга | Дифференциальные операции в криволинейных координатах |
| Интегральные теоремы для векторов и тензоров | Температурное поле и поле теплового потока |

