Оглавление:



Компоненты малой деформации
- Компоненты малой деформации Обозначим ех, ЕС, ег-относительная линейная вариантов элементов, параллельных вариантов по осям X, Y и Z. СЦК, СЦК, СЦК-относительный сдвиг. Индекс U означает ось,
элементы которой параллельны, где прямой угол смещен. Относительный сдвиг считается положительным, если прямой угол между элементами уменьшается во время сдвига.
Компонент деформации представлен смещением точек u, V и w вдоль осей x, Людмила Фирмаль
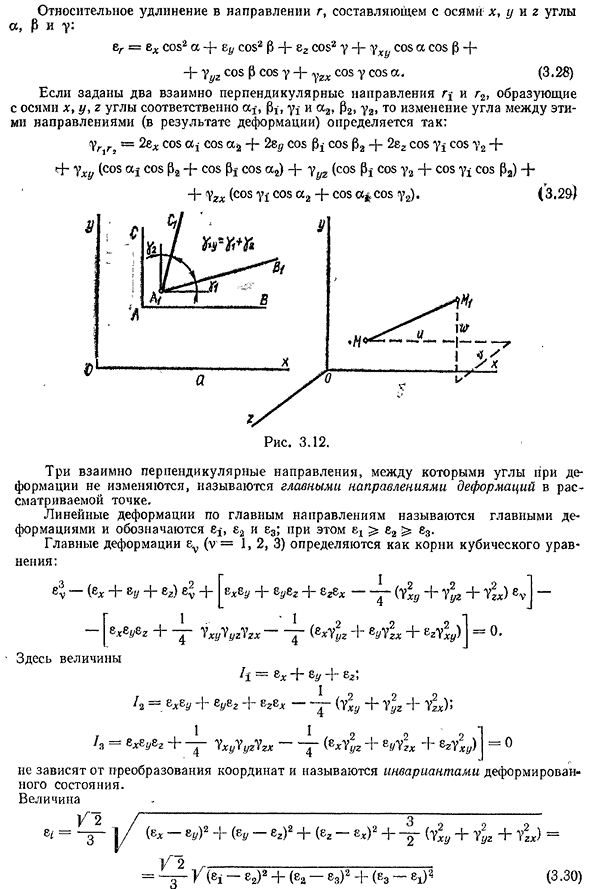
y и z(рис. 3.12, б): ди ДВ. ДГ, еДХ ’е г~У’ Е Г ~ ДГ ДВ, БиДХ~+~ду б, ДВ Ди ДГ U сеть U сеть U УГ=~дю~+ДГ ’ тьфу=~ДГ+ДХ(3-27) Состоит 40the с расширением направления г, ось Х, Y и G сгибает, Р и г: ЕР=ех coss2 4-е; cos2P+эз coss2 г, г, потому что acosf3+4-г^п, потому что потому что потому что У4-угол: (3.28)изменяет угол между этими направлениями
осей X, Y и Z угол 04, Р И2, з, П22 угол, У2 дали два направления, ый, потому что А2+потому чтопотому, У2). (3.29) Три взаимных вертикальных направления, в которых угол не изменяется при деформации, называются основным направлением деформации в рассматриваемой точке. Линейный вариант основного направления называется основным вариантом и обозначается как ex, E2,
- E3 и обозначается как 14Js E2Js E3. Основной вариант sv (v=1,2,3) определяется как корень кубического уравнения: е в — (ех т т е г)е в+EXE4>+ & 4>ez4~6^ Г Один. Один. —э-хе я/и Z+, где значение 4 (уху+Ууг»г тьфу)Эв Ukhuugh~~~(е^з+ЕУ y2zx+изи^)=0. — ex + EU+Eg’, — f-EU eg ex — — — — — — (UX u4-u2U g4-u|%); 7z=ex eueg4-Uhuugugh—u+&gu2a d)=0 не зависит от преобразования координат, называется инвариантом деформационного состояния. Е я=^ — Г-й/ «, например/)2+(е-е) 2+(е-е*) 2+(КК+У2)+?Л=) =К ф е-е-е)2+(э-эз)а+(эз~Е1)’(3.30) 41называется прочность на деформацию. Или eg=U2uo CT, где uoct= — (E2-E2)2+(E2-E3) 2+(E3-e^2 называется октаэдрическим сдвигом,
а ffz=3GZ>(3.31), где G-модуль сдвига октаэдра, который представляет собой зависимость между угловой вариационной напряженностью и напряженностью деформации октаэдров между направлением касательного напряжения и направлением главного напряжения. При движении в любом направлении, например, в направлении оси Z, а ось без зависимости от координаты G равна нулю, такая деформация является плоской. Деформационное состояние в точке плоской деформации описывается такой приведенной зависимостью, что соответствующий член в этом случае становится равным нулю.
Для исследования деформационного состояния в терминах случая плоской деформации иногда удобно использовать графический Людмила Фирмаль
прием, представляющий собой структуру кротового круга(рис. 3.13). Период задержки по оси X прямоугольной системы координат ODj=ex, OD2=точка O, перпендикулярно-MS g1larue задержка отрезка Di E=u u u u u, а O2-отрезок d 2E= — y ear. По прямой линии EF на диаметре, окружности поперек абсцисс точек A и B, то строится отрезок OA==e!, OV=E3-основной вариант. Направление основного удлинения задается прямой линией B, образующей угол a относительно оси поперечной оси. Напряжение сила и — = — г(1+п)Ex и чистого сдвига (например,=ЕС=Е2=Ууг=тьфу=0,СЦК#=0) ВГ — = — Ух л
Смотрите также:
| Объемное напряженное состояние | Зависимости между напряжениями и деформациями в пределах упругости. закон Гука |
| Круги Мора | Относительное изменение объема |

