Оглавление:


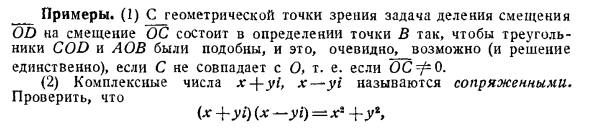

Комплексные числа
- Комплексный номер. Так же, как смещение {x:] вдоль OX соответствует точке () или действительному числу x, смещение [x, y] на плоскости представляет собой точку (x, y) или пару вещественных x, y Это соответствует. Удобно указать это действительное число x, y в паре с символом. х + й Причина выбора такого обозначения становится еще яснее. Тем временем читатели должны рассматривать x — \ — yi как еще один способ написания букв [x, y]. Символ x — \ — yi называется комплексным числом. Затем перейдите к определению сложного равенства, сложения и умножения. Каждое комплексное число соответствует смещению.
Сумма и произведение двух комплексных чисел является комплексным числом, соответствующим сумме и произведению соответствующих смещений. Вот так x + yi = x ‘+ y4 (1) Только когда x = x ‘, y = y’. (X + y [) + (X ‘+ yC) = (x + l:’) + (y + /) /, (2) ( + Yi) (* ‘+ //) = xx’-yy’ + (xy1 + yy) L (3) Как частный случай из (2) и (3) вы получите: x + y1 = (* + ° 0 + (0 + y0, (x + 00 (x ‘+ y’i)) = xx’ + xy’C Эти отношения показывают, что при работе с комплексными числами вам не следует бояться недопонимания при записи x вместо x -} — 0 / и yi вместо 0 — \ — yi. Читатель может легко проверить, что сложное сложение и умножение следуют законам алгебры. Закон алгебры выражается следующими соотношениями. (X + yi) + (x ‘+1) = (Y + y’1) + (* K * +3 «‘) + (‘ + Y 0} + (» + Y «1) = (* + yt) + -HC * ‘+ Y0 + (* «+ *» #}.
Два комплексных числа эквивалентны, если их соответствующие смещения равны Людмила Фирмаль
{x + yi) (* ‘+ / i) = (X- + y’t) (X + yi), (x + yi) {(‘ + y’i) + (x ‘+ Y0} = ( X + yi) (Y + yi) + {(X + yi) + (x ‘+ y0 J (x «+ / • /) = (X + yi) (x’ + y» i) J- (.X + 3-0 {( ‘+ / 0 (* «+ Y» 0 (= f (* + yl) {X + Y0} (* «+ y» i), Свидетельство фактически идентично доказательству соответствия между уклонами. Комплексное вычитание и деление определяются как обычная алгебра. Так определите (x-j-yl) — (* +> — 0 + {- (* ‘+ / 0} = * + yi + (- / О = (х-х’) + (у-У) 1 или то же число 5 — | -Это (* ‘+ Y0 + a + h9 «= * +> * • Наконец, (x — \ — yi) j (x — \ — y’i) определяется как комплексное число -yj /. + = или x’t-y’h \ 4- (x’t {+ / $) i = l: + yi, или xh-y \ = x, x’z + yh = y. (4) Решение этих уравнений для £ и yj дает: p_xx ‘-j-yy’ _yjf-hu ‘ JC’S4-y * 9 X * + y * ‘
Это решение не имеет смысла, если x ‘и y’ оба равны нулю, то есть x ‘- \ — y’1 = 0. Поэтому вычитание всегда возможно. Деление всегда возможно, кроме случаев, когда делитель равен нулю. Теперь вы можете определить положительную целую степень комплексного числа x — \ — yit полинома x- \ ~ yi и рациональную функцию x4-yi как нормальную алгебру.
| Геометрические места в пространстве | Геометрическое толкование умножения на i |
| Смещения вдоль линий на плоскости | Уравнения z*-{-l =0 |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Пример. (1) С геометрической точки зрения проблема деления смещения OD на смещение OS заключается в определении точки B так, чтобы треугольник COD и BWT были похожи, и если C не совпадает с O, это явно Да (и решение уникально). е. Для OS ^ O (2) Комплексные числа x + yl, x — yi называются сопряженными. Пожалуйста, проверьте (Qi + yi) {x-yi) = x + y Следовательно, произведение двух сопряженных чисел вещественно, x + yl _ {x + yi) {x ‘-yC) XX’ — \ — yy ‘-f (x’y-xy’) 1 x ‘+ y’l (xG + y’1) (x’ — Ну 40. Одно из наиболее важных свойств действительных чисел включено в следующую теорему. Если произведение двух чисел не равно нулю, произведение не будет равным нулю.
тогда xCh — y’i1 = 0, x \ + yCh = 0. Из этих уравнений $ = 0, yj = 0, то есть 8 + ^ = 0, Если нет уравнения: x ‘= 0 и y’ = 0, т.е. x ‘y’i = 0 Следовательно, x + yi не будет нулем без одного из чисел x ‘. ~ \ -Y’1 или £ + v не исчезли. 41. Уравнение n: согласился упростить обозначения, написав x вместо a = -1 x + 0 / и yi вместо 0 + yi. В частности, просто представляйте комплексное число 11 с i. Это числовое значение, соответствующее единице смещения по ОК. Есть также следующее: P = ii = (0 — (- 1r) (0-1-1 /) = (0 • 0-1. 1) + (0 • 1 + 1 • 0) i = -1.
Чтобы показать, что эта теорема справедлива для комплексных чисел, установите = 0, ^ = 0 в уравнении (4) в предыдущем разделе. Людмила Фирмаль
Аналогично, (- /) 2 = -1, поэтому комплексное число / u-i удовлетворяет выражению x2 = -1. Читатель говорит, что правила сложного сложения и умножения просто сводятся к тому, что действия над комплексными числами выполняются точно так же, как действительные числа, и символ i также считается числом, но произведение con = -on- везде 1 9 происходит. Например (X + yi) C * ‘+ yy) = xx + xyi + yx’i + yyY = (xx’yy’) + (xy ‘+ yy’) L

