Колебательное движение

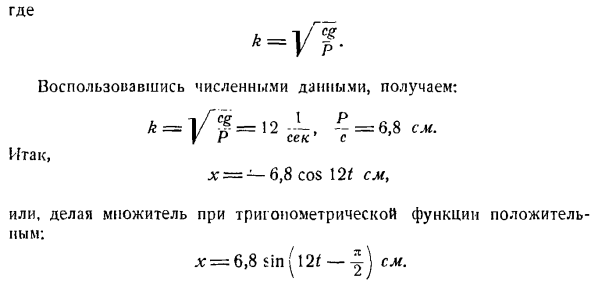
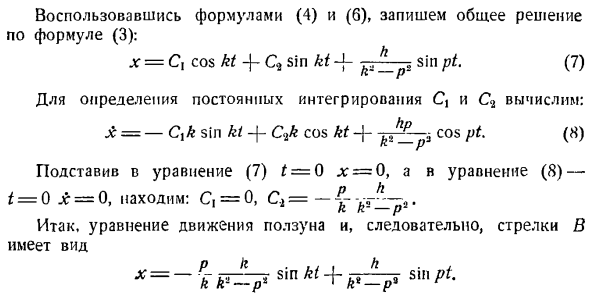
Колебательное движение

• Колебательное движение 1°.Восстановите питание. Теория колебаний является одной из важнейших областей теоретической механики. Его роль в современных технологиях растет. При проектировании двигателей, машин, механизмов, мостов и других сооружений во все времена Выполнен расчет вибрации. В этом разделе рассматриваются простейшие задачи линейных колебаний точки масс (крутильные колебания описаны в главе IX, а малые колебания системы точек масс описаны в главе XIII).

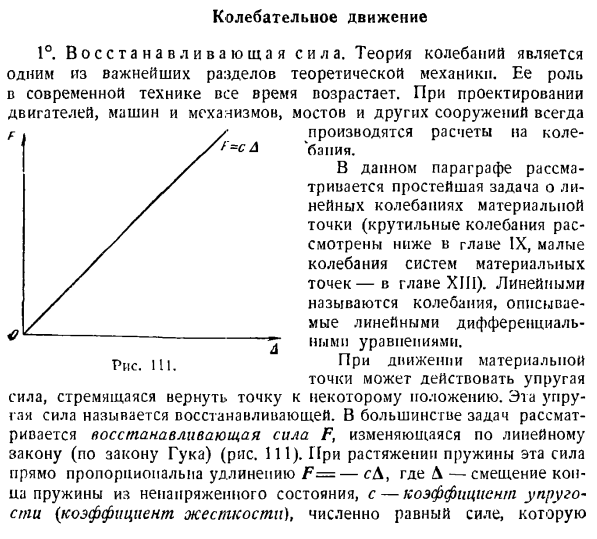
Линейные колебания описываются линейными дифференциальными уравнениями. Когда материальная точка движется, действуют упругие силы и точка стремится вернуться в определенное положение. Эта упругая сила называется regenerative. Восстанавливающая сила F изменяется по линейному закону (по закону крюка) (рис. 111).При растяжении пружины эта сила прямо пропорциональна удлинению F = — cA. Где\ — смещение конца пружины из безнапряженного состояния, с-модуль упругости (модуль жесткости), численно равный силе.

In в большинстве задач рассматривается восстанавливающая сила F. Людмила Фирмаль

У С Л Фигура болезни. из статического положения равновесия xQ смешивается, сообщается начальная скорость в том же направлении, и материальная точка отклоняется к точке A в первом указанном направлении (см. кривую/на рисунке 115), а затем асимптотически приближается к положению равновесия (без прохождения).） ） x = jc0> 0 x = x0 <^ 0 (и| 1 (π+ Vn * — k))», то есть, если в начальной точке материальная точка смещается из положения статического равновесия на x0, а модуль упругости переносится на указанную выше скорость неравенства, то качество переходит в положение равновесия в противоположном направлении (см. кривую 115 / отклонение на рисунке) и приближается или не проходит через） ） для JC = н:0 х = 0×0 ^ 0 

(Кроме того, j Xq I Oo (π — / — V-k)).То есть в первой точке материальная точка смещается от положения равновесия на jc0 и составляет 115. Старт без начальной скорости Либо модуль перемещается в направлении, противоположном начальной скорости, удовлетворяющей указанному неравенству, либо материальная точка приближается к положению равновесия асимптотически, не проходя через него (см. кривую III). В случае Bo ucex 3 движение быстро исчезает. c) n = k является ограничительным случаем. Масса совершает затухающее апериодическое движение: x = e-nt (Q + Q0 * tco, если x становится неопределенностью типа 0-oo.

• Если вы откроете неопределенность в соответствии с правилом логарифма, вы получите lim l:= 0, что указывает на распад. / * ♦00 Движение. В начальном состоянии заданного движения (t = 0 x = xQ)x = ^ xa круговое уравнение имеет вид: х = е-НЛ \ х0 + F (А * О + Л * О) Т]. Характер демпфирования зависит от начальных условий. если x = x0 ^ xO x = x0 ^> 0, то движение массы соответствует кривой/. если η=π0> 0,= = Xa <0 (и|η<0 / о), то движение массы соответствует кривой II. для η ’=π0> 0, x — Xq = 0 или x0 <0 0(далее| xQ | <n nxQ) движение массы соответствует кривой///.

Во всех 3 случаях движение быстро затухает. Решение задачи о свободном колебании точки массы лучше осуществлять в следующем порядке: 1) Выберите точку отсчета и возьмите начало координат в положение статического равновесия точки массы. 2) Запишите начальные условия движения точки масс. 3) установочная сила, приложенная к материальной точке, показана на рисунке. Применение принципов прощения связей увеличивает силу реакции связей. 4) построить дифференциальные уравнения движения точки массы в проекции на соответствующую ось. 

Использовать начальные условия движения для интегрирования дифференциальных уравнений движения и определения интегральной постоянной. Людмила Фирмаль

Для определения круговых частот колебательных периодов T и TR pet, k v \ kR w необходимо интегрировать дифференциальные уравнения motion. It достаточно отредактировать дифференциальные уравнения движения, определить коэффициент K’1 в координатах, коэффициент c2n в проекции скорости x-и вычислить окружное волновое число и период колебаний по приведенной выше формуле.

При создании дифференциального уравнения необходимо нарисовать массу в промежуточном положении, соответствующем ее положительным координатам. Предположим, что точка движется в направлении увеличения этой координаты. После создания дифференциального уравнения движения (инпараграф 4) необходимо рассмотреть статическое равновесное состояние колеблющейся материальной точки. Это условие можно использовать для уменьшения числа постоянных членов в правой части дифференциального уравнения.

Если рассмотреть задачу о развертке колебаний точки массы при отсутствии сопротивления, то в общем виде можно привести решение к результату и подставить численные данные в it. To решая задачу о свободном колебании точки массы при наличии сил сопротивления, необходимо определить n и k, заменив численные данные составленными дифференциальными уравнениями. , Большое сопротивление и крайний случай). Выпуск 244.Груз массой P = 9N g подвешивается на конце пружины, которая находилась в первом умите, который был неподвижен в деформированном состоянии, и отпускается без удара.

Найти уравнение вибрации нагрузки, если известно, что для деформации 1 см пружины необходимо приложить усилие 14,4 г модуля упругости. Решение. направьте ось x вертикально вниз и возьмите опорную точку в положении статического равновесия нагрузки. В более раннее время нагрузка подвешивалась к концу несформированной пружины, что было, следовательно, выше положения статического равновесия при величине статической деформации пружины П Dst= -, где c-модуль упругости пружины. Нехватка Первые мгновения шока указывают на движение без инициала speed. So, первый Транспортная ситуация груза находится в виде: п / = 0 x = xQ = -, x = xft = 0 (ось X имеет знак минус.

Это было вызвано тем, что ось l была вертикально вниз, и начальная нагрузка была выше положения статического равновесия.) Он указывает нагрузку в смешанном положении относительно пули pa x и предполагает, что x движется в направлении увеличения, т. е. downward. In в этом случае пружина растягивается, и ее упругая сила F (восстанавливающая сила) равна F = — c A. где A-смещение конца пружины из безнапорного состояния, то есть LX = M0M = Dst-rLG. So … Гонка FX = — с(ДСТ-к*).Да.） Перейти к выпуску 244. Кроме того, в силу своего веса Р. применять ФГ к нагрузке. создайте

дифференциальное уравнение для движения груза, спроецированного на ось X. (2） МХ = п + ф、 При применении Формулы(1)、 х = П-cDgt-СХ. П. С. (3） с. Рассмотрим нагрузку в положении статического равновесия. Нагрузка приложена со статической упругой силой FCJ, то есть FC1 = cDst, которая появляется, когда нагрузка Ru вертикально вниз и нагрузка растягивается DST под действием нагрузки. Упругая сила FCJ вертикально вверх. От состояния равновесия нагрузки зависят: П-Ф, Т = 0、 ул Иначе говоря Используя этот результат, запишем

дифференциальное уравнение (3) в виде: Х-ф-к? x = 0, (5） Куда? * — С. Дифференциальное уравнение (5) свободной вибрации груза представляет собой линейное однородное уравнение 2-го порядка с постоянным коэффициентом. Форма характеристического уравнения имеет вид Корни характеристического уравнения мнимы: XJ 4 = Lfc&I. Таким образом, решение уравнения описывается следующим образом: Л; = С, потому что КТ-ф ка грех КТ. (6） C /

и C *расчет для определения интегральной константы： х = — С \ к греху КТ + дь, потому что КТ. (7 )） (6) Замена начальных условий движения： Выяснить f = 0 x = xQ, и (7) i = 0 x = xQ = 01С\ = xQ=—, С-0. Уравнение для движения груза после подстановки значений Cj и C (6) имеет вид、 п х =соѕ КТ、 И Куда? Когда вы используете числовые данные, это выглядит так: x =-6,8 cos 121 см、 Или сделав тригонометрический показатель положительным： l; = 6,8 sin ^ 121 -^) см. Сравнивая полученные результаты с уравнениями свободных колебаний, записанными в общем виде x = a sin(kt — \ — a), можно видеть, что амплитуда колебаний равна a = 6,8 см, начальная ф

аза колебаний равна a= -, а круговая частота колебаний равна k = 12. Считанные секунды Период колебаний груза определяется по формуле — 2К 2г. __ T-k-j2 = 0, O2 секунды Эти результаты могут быть получены непосредственно с помощью выражений. я= | / *; + |; =？= 6,8 см, и = арктан = арктан (- ОО)= -. Проблема 245.Под действием подвешенной нагрузки на край пружины пружина получила статическое удлинение Dst = 5 см. Если в первый момент возникла нагрузка в состоянии статического равновесия, то найти закон вибрации этой нагрузки пружины Начальная скорость движения

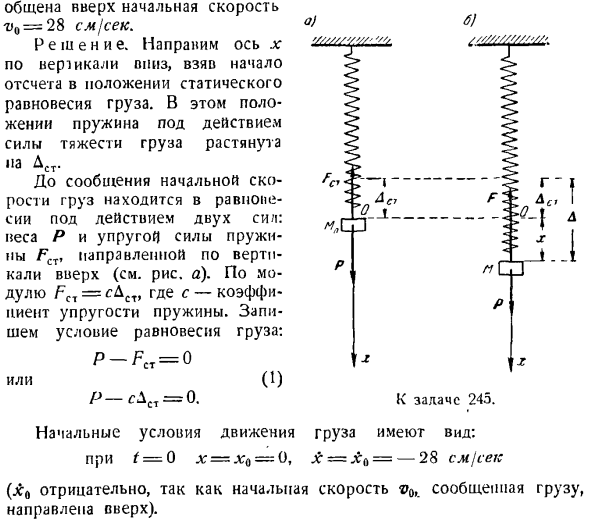
вверх равна-u0 = 28 см/с. Решение. возьмите начало координат в положение статического равновесия нагрузки, с осью x, обращенной вниз vertically. In в этом положении пружина под действием силы тяжести груза растянется и станет ДСТ. б） Проблема 245. Да.） До тех пор, пока не будет сообщена начальная скорость, нагрузка находится в равновесии под действием 2 forces. It является восходящей пружинно-упругой силой, Fcx, перпендикулярной весу P (см. Рисунок

A).Модуль FC1 = cDst, где c-модуль упругости пружины. Опишите критерии балансировки нагрузки. Или П-ф ст = 0 0.） ПК \ л = 0. Начальные условия движения груза следующие: t = 0 x = Xq = 0, x-X(> =-28 см / с (Начальная скорость, указанная для нагрузки, направлена вверх, поэтому jc0 отрицательна.)

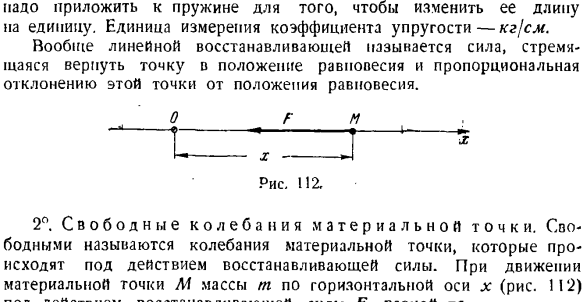
Чтобы изменить длину на 1, нужно приложить ее к пружине. Единицей измерения модуля упругости является кг/см. В общем случае линейная восстанавливающая сила называется силой, которая пытается вернуть точку в ее равновесное положение, и пропорциональна отклонению этого положения от ее равновесного положения. О Ф М Рисунок 112. 2°.Свободное колебание точки масс.

Свободой называют колебание точки массы, которое происходит под действием восстанавливающих сил. Когда точка масс M массы m движется вдоль горизонтальной оси x (рис. 112） Положительная абсцисса x показывает промежуточное положение L1, соответствующее нагрузке (см. Рисунок B).в этом случае пружина растягивается до A = ACT -} — jc, а упругая сила F (восстанавливающая сила) направлена вертикально вверх. И затем… Вы можете использовать следующее (2） Помимо упругой силы F, нагрузка P. создает дифференциальное уравнение для движения нагрузки

в проекции на ось X. — И3?= ЗП + Форекс. Используя формулы (2) и (1), получаем: * + =(3） Куда? Непосредственно вычислить k *невозможно, так как коэффициент упругости от пружины неизвестен. Присвоить выражению (1) p = mg, что выражается в виде — = — 5 -. So… Ш акстись (Dst в постановке задачи показан.) Интегрирование дифференциальных уравнений(3) не является сложным. Создайте соответствующее характеристическое уравнение X * — j — £4 = 0.Отсюда корни характеристического уравнения X ^ =±kL мнимы, поэтому решение уравнения принимает вид: (5） х = ОЖ, потому что

КТ Си, грех КТ. Чтобы определить интегральные константы Q и C\, найдите: х = — дь грех КТ + CJt потому что КТ. (<>） Присвоить формуле (5):^ = 0,x = x0 = Ot и формуле ((i):/ = 0,x = xQ. Тогда C,= 0,= (Таким образом, формула (5) имеет вид х = * » грех КТ. (7 )） Используйте числовые данные для получения следующих данных: педсоформирование пружин. Если в первый момент вы смещаетесь на 4 см от положения равновесия ипрапо, а начальная скорость 90 см / с сообщается с правой стороны, найдите периодичность гравитационного уравнения и колебания нагрузки. Решение.

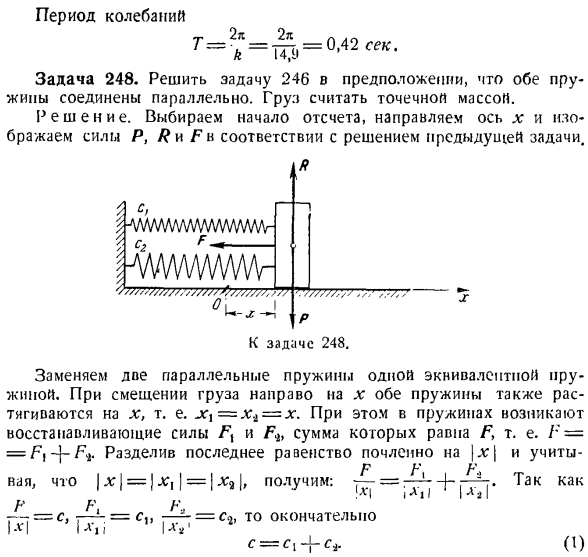
направьте ось x горизонтально вправо и возьмите точку отсчета в положении равновесия груза. Опишите начальные условия движения товаров. / = 0 l: 0 = = 4 см, Ko = 90 см / сек Представьте себе, что из точки отсчета он показывает нагрузку промежуточного положения, смещенную на l вправо, и направление, в котором x будет увеличиваться, то есть двигаться вправо. В этом случае правая пружина сжимается x, и ее упругая сила направляется к бледно-желтому цвету color. At при этом левая пружина растягивается до l. следовательно, ее упругая сила Fy также направлена влево. Ф] В = С}

ху Ф, Х =-Схх. 2. в дополнение к восстанавливающей силе Fx и Fb, весу P и нормальной реактивной силе f? Гладкая плоскость. запишите дифференциальное уравнение движения точки массы в проекции на x-axis. In в этом случае, это будет выглядеть так: П-х = FXX на + фу, или J л)=-(КТ + СНХ.(1） Как следует из дифференциального уравнения(1), обе пружины могут быть заменены на 1 эквивалентную пружину, модуль упругости которой равен сумме коэффициентов упругости этих 2 пружин, то есть c = c1.- \〜 £+ к * Х = 0, (2） Куда? Р-р.

Создайте характеристическое уравнение, соответствующее дифференциальному уравнению (2): k1-0, из которого Xl4 = it ki. Таким образом, форма решения уравнения(2) имеет вид х = С \ потому что КТ-Ф Ци Син КТ. (3） Вычислите x = — С\ k sin kt-j-С, Лcos kt, чтобы определить интегральные константы Q и Ca. (4 )） Подставляя Формулу (3)/ = = 0, x = x0>и Формулу (4) 2 = 0, x = n * o>, получаем Cj = xQ} Q = — g. уравнение (3) принимает вид: икс х = х0 соѕ КТ-Ф-грех КТ.

(5） Поставь ЯФ ХЖ = грех, −0 = а потому что,(с） Где А и А находятся constants. In в этом случае уравнение вибрации нагрузки(5) может быть выражено следующим образом: Х = а \ п(т + а). (7 )） Амплитуда колебаний a и начальная фаза колебаний a определяются из одновременных уравнений (b). а = ЧХ\, (8） =(9） Используя число, получаем его из Формулы (2). ; / Е «- М»)Г-ла(4 ч-5) ■ 980 _ J_ Л — ^ П-Дж / 9.8〜 Из Формулы (8): из Формулы (9)： х0 30-4 4 Откуда 4. a = arctg-j = 0,92 Радиана. Таким образом, закон колебаний нагрузки задается

следующей формулой x = 5 sin (30£ — J-0,92) см, а период колебаний Задача 247.Решите предыдущую задачу, исходя из предположения, что обе пружины соединены последовательно(см. рисунок). Я с, С2 ф п Б / М / М / НМ /?////////// ?// * /////////// п Проблема ’ 247. Решение. Ось отсчета x принимается в положении равновесия нагрузки с недеформируемой пружиной. направьте ось x горизонтально вправо. Начальные условия эксплуатации остаются прежними. t = 0 x = xQ = = 4 см, x = jc0 = 90 см /с давайте покажем смешанную среднюю

позицию нагрузки справа от x. In в этом случае левостороннее восстанавливающее усилие F возникает в пружине. Вычислите модуль упругости от пружины, эквивалентной заданным 2 пружинам. Полное удлинение пружины равно смещению груза, то есть Когда груз смещался на x вправо, каждая пружина растягивалась. Общее количество этих расширений равно\ x\, то есть М = 1 * 1 | + S-(2）

Каждая пружина растягивается под действием силы F、 1 * 11 = г. 1 * 1 -? (3） Подставляя выражения (1) и (3) в выражение (2), получаем: Ж + я- Противоположное значение коэффициента упругости (жесткости) называется коэффициентом пластичности. Поэтому, когда пружины соединены последовательно, податливость эквивалентных пружин равна сумме приспособляемости этих пружин. Из Формулы (4) находим модуль упругости эквивалентной пружины. с =(5）

В дальнейшем вместо 2 данных для последовательно соединенных пружин рассмотрим 1 эквивалентную пружину с модулем упругости c. Когда нагрузка смещена на x вправо, проекция восстанавливающей силы F влево равна С GX = — СХ = — с-fiftj.*(6） В дополнение к силе F к нагрузке прилагаются следующие силы: P-ее вес, # — вертикальная реактивная сила гладкой горизонтальной плоскости. Составьте дифференциальные уравнения движения груза

в проекции h; I-ось x： C1 м£ = FX или МХ = — — — х. * с 1 + С2 Перепишите полученное уравнение следующим образом: х — (■*к * Х = 0,(7） Здесь._ к = −14.9 л. (8） В КТ КС П сек.} Легко найти истинное тождество дифференциального уравнения (7) и дифференциального уравнения (2), полученного в предыдущем примере problem. So, можно обойти промежуточные вычисления и записать ответы, основанные на формулах(7), (8)и (9) предыдущего вопроса. * = ЧХ я + 2 = V42 + [Т = 7.25 ига = СФП = я ^ Лл = 0.66 ф я = arctg 0.66 = 0.58 рад х = 7.25 грех (14.9 / + 0.58) см Под действием восстанавливающей силы F, x \ \ \ \ \ 4V \ Module F = c \ x (О-точка равновесия ki M), образуется дифференциальное уравнение движения Х-ф&х = 0 л. — G С, где К1—. До тех пор В случае колебания массы m точка M подвешена к нижнему концу пружины, где верхняя часть прикреплена к потолку, упругая (восстанавливающая) сила F направлена вверх, когда точка M движется вниз(рис.113), а Fx = — c(Lst + dg), где Ast-статическое растяжение пружины под действием оси x, направлена вдоль оси пружины в направлении натяжения, то есть вниз. Опорная точка на оси берется в положении статического устройства. От. Вес материала пятна M нависает над пружиной. Когда опорная точка выбрана таким образом, дифференциальное уравнение для свободного колебания материальной точки имеет вид: Йк + к * Х=: О、 Где k*= -. т. При начальных условиях движения массы, записанных в виде： при t = 0 x-xn, x = x0 закон свободных колебаний имеет следующий вид: х = грех (к-т с-）、 Цикл вибрации Выпуск 248.В предположении, что обе пружины соединены параллельно, решается задача 246.Рассмотрим нагрузку как точечную массу. Решение. В соответствии с решением предыдущей задачи выберите опорную точку, укажите ось x и укажите силу P, Ru Fu. Р Перейти к выпуску 248. Ноль \ Х — » −1 Р Замените 2 параллельные пружины на 1 эквивалентную пружину. Если нагрузка перемещается вправо на x, обе пружины также растягиваются на x. то есть jc \ = x ^ = x. In в этом случае восстанавливающие силы T7 и/ \ 2 возникают в пружине, сумма которых равна F, или/. = Fi — \ — F * разделить последний член равенства на члены / lg |и учесть \ х \ = \ ХХ | = / л; в：- ФФ. j — ; = = С%, — = Со, И, наконец, Что? в / УФ-1 JL. 1 * 1 / да| ■ С — j- Да.） Так, если пружины соединены параллельно, то модуль упругости эквивалентных пружин равен сумме коэффициентов упругости этих пружин. Последующий ход решения задачи повторит решение предыдущих 2-х задач. Используйте формулу (1), чтобы сразу записать конечный результат. * = к- G. £ * l G I 90 * r*=] / Ho+=] / 4 + zo * = 5 см> а-arctg = равенства arctg ^^ = равенства arctg 4 = 0.92 / Ми), ДГ = 5 грех(30т + 0.92) см、 7 = 1 = 1 = 0.21 ^. Так, если пружины соединены параллельно, то модуль упругости эквивалентных пружин равен сумме коэффициентов упругости этих пружин. Последующий ход решения задачи повторит решение предыдущих 2-х задач. Используйте формулу (1), чтобы сразу записать конечный результат. * = к- G. £ * l G I 90 * r*=] / Ho+=] / 4 + zo * = 5 см> а-arctg = равенства arctg ^^ = равенства arctg 4 = 0.92 / Ми), ДГ = 5 грех(30т + 0.92) см、 7 = 1 = 1 = 0.21 ^. (При выполнении конструкции, соответствующей этой задаче, необходимо предусмотреть отдельную направляющую для каждой пружины.） Задача 249.Груз весом Р = 98 г, подвешенный на конце пружины, перемещается по жидкости. Коэффициент жесткости пружины c = \ 0g / см. Сопротивление движению пропорционально 1-й степени скорости груза: R = $ v, где p = 1,6 gsec / cm. At в первый момент находим уравнение движения груза, когда груз движется вниз на 4 см от положения статического равновесия, а начальная скорость vQ = 4 см / scc передается. Решение. направьте ось x вертикально вниз вдоль пружины и возьмите точку отсчета в положении статического равновесия нагрузки.

Опишите начальные условия движения товаров. £ = 0 x = xy = 4 см, x = x0 = 4 см; ЦСК. Предположим, что абсцисса x показывает нагрузку в положительном положении. Поскольку пружина подвержена расширению D = Dst — / — lg, проекция упругой силы пружины F на ось x направлена вертикально вверх. (О Гонка FX = — с(ДСТ+*). — Предположим, что нагрузка движется в направлении, в котором абсцисса x увеличивается. Нагрузка па-к задача 249 сопротивление

движению R направлено в противоположную сторону к скорости. То есть это вертикально вверх. Кроме силы F, П. нагрузки к нагрузке. МХ = Р- \ — FX с + Подставляя в это уравнение значение Rx =-$ vx и формулу (I) Fx, получаем следующую формулу: (2） (3） Полигликомплекса = Р-С \ Т \ СХ-телефонов vvx. Это легко увидеть. ПК \ М = 0. Фактически, в положении статического равновесия к нагрузке прикладывается следующая сила. P-вертикальный нисходящий вес, и статическая упругая сила пружины Вертикально. Поскольку нагрузка находится в равновесии, P-FCT = 0, за которым следует

уравнение (3). Первые 2 члена в правой части дифференциального уравнения (2), основанные на уравнении (3), отбрасываются. Если вы замените vx на x в последнем члене, это выглядит так: НТ-Ф-2nJt-к * Х = 0, (4） Куда? б-лчх $ н-ш. к-р, н-2 р Подставляя числа, мы видим, что£= 10 S-x, n = 8 sect1), таким образом, n <^ k (для низкого сопротивления). Опишите характеристическое уравнение

дифференциального уравнения(4): X92nx-(- £4 = 0, где \ l q = — n± / n-k * = — n±i / / r * — n \поэтому уравнение движения груза будет иметь вид: х = е-НЛ(С, что /£4 -/?Т + С9 грех / * 4-н * т) (5） Для определения интегральной константы x = <hL(-C, sm t + — Ф С2-#COS в / К * * н * т) — не-НТ(вопрос потому, что /£4-l41-Ф + C9sin / ТФ-ИФ). (6） Если вы назначаете выражение (5)£= 0, x == xQ}и выражение (6)^ = 0、 £!Их получаем (x-xQ): CI = Ar0, присваиваем значение= C、 Уравнение (5) C2 имеет вид: х = Ю. Г. «(r0cos-н * т + гг = = ДЖП грех — (7） Преобразуйте полученный результат equation. To сделайте это,

войдите: Хз, Н. ве ХЖ = грех, __ ^ = а потому что, (8） Где L и a-константы. Из (8)легко найти ^ / ^ Т + Ш (9） Уравнение(7) принимает вид: х = Ас НЛ грех(/ КЛ-Р? т + а). (11） Время движения ослабляет нагрузку на круговой частоты (Т— * О-0 и позже） КРЗ = ВКТ = л? (12） Амплитуда колебаний a — это коэффициент r, обращенный к синусу формулы (11). а = ас-НТ (13） Где а определяется по формуле (9). Выше мы обнаружили, что= = 10 ck — \ n = 8 ckk. Из условий задачи Λ* 0 = 4 см; jc0 = 4 см /с уравнение этих чисел（9）、（10）、（12）、（13）Если вы назначаете, a = 7.2 cm} a = 0.59 rad,/ e /? = 6 секунд — \ а-7.2 е »

8ф см. Поэтому нагрузка выполняет демпфирование колебаний по закону * = 7,2 * » * см. sin (6 * + 0,59) (14 Период колебаний нагрузки равен= ^ = ™ = 1,05 секунды. (Если Когда нагрузка вибрирует при отсутствии сопротивления, период колебаний сокращается. Действительно, по формуле G = получить 7 = 0,63 секунды） Амплитуда колебаний нагрузки а = 7,2 с — * г см уменьшается экспоненциально. Предположим, что момент времени ag соответствует первой амплитуде ag. Следующая амплитуда ai + l возникает после половины При делении a; +1 па,、 7 * = 1,05 секунды, так что^ = e » 4 ′ * ^ 0,02. Таким образом, последовательность амплитуд, знаменатель<7″=?Он образует равный ряд, который

бесконечно уменьшается при 0.02. Проблема 260.Решите предыдущую задачу, исходя из предположения, что сопротивление движению R =здесь[3 = 5.2 gssk / cm. At в первый момент нагрузка была смещена от статической При равновесии 4 см начальная скорость движения вверх была равна * y0 = 240 см/с. Решение. опорная точка на оси x все еще находится в положении статического равновесия нагрузки, а ось

x находится вертикально downward. In в этом случае исходными условиями для перемещения груза являются следующие: f = 0 x = xQ = L см, x = x ^ = −240 см / с (L ’ 0 отрицательно, потому что начальная скорость направлена вверх.) По решению предыдущей задачи получаем дифференциальное уравнение движения груза(см. уравнение предыдущей задачи (4） Куда? Б-л г ** — В П — ’ — 2Р * Подставляя числа, вы получаете:£ = 10 секунд ’1, n = — * 26 секунд’; следовательно, h (для высокого сопротивления).Создайте

характеристическое уравнение: X-|-2 /Л -| — Л4= 0, whice Х,= — п-к \ х. 2 = — н -\ — / Х4-к \ поскольку k, корни X и X *являются реальными и отрицательными. Форма уравнения движения груза выглядит следующим образом: х =(1） Для определения интегральных констант CT и С2, вычислить: Х = Ц ^ в + с. 2 раза, * ХД. (2）

То есть, масса совершает гармонические колебательные движения. Где а-амплитуда колебания-максимальное отклонение точки колебания от положения равновесия КТ — \ — А. Эта фаза колебаний и начальная фаза колебаний определяется из исходных данных. L0 k-круговая частота колебаний-частота значимых точек при 2g: секунда： Круговая частота колебаний не зависит от начальных условий движения (π0 и’0).Эта характеристика называется

изохронизмом, а вибрация — изохронизмом(амплитуда а и начальная фаза а колебаний зависят от начальных условий движения). Период колебаний t точки — это минимальное время, после которого точка имеет те же координаты и ту же проекцию скорости. Диапазон вибрации — это расстояние между экстремумами точки вибрации. Диапазон колебаний будет равен 2 амплитудам колебаний. Если подставить уравнение (1)/ = = 0, x = xQ, а уравнение

(2) f = 0, x = xQ, то получится система уравнений. = Г — {- С2; ^ «о = — б Откуда? /-«_ ^ О — ^ О — / -> 1 А А, — Л, — Л、• Уравнение (I) C1 и C. Если вы замените вычисленное значение 2, вы найдете уравнение переноса нагрузки х =-а) — о-■* <>）]•（3） Значение X и X. используйте а и гиперболические функции для описания уравнения движения (3) в виде: * = , / 1-к * » + ШБ в ^^ Т + г р—ИГ _ _ + JC0 V n * —

ch J / V-L (4） Движение груза апериодично и далее ослабляется. После подстановки чисел в Формулы(3)и(4): n = 26 секунд — \£= 10 seng19×0 = 4 cmu<, =-240 см /с x = — e — * «(29 > co, мы можем видеть, что уравнение (3) имеет тип 0-co uncertainty. In для того, чтобы раскрыть неопределенность, мы применяем больничные правила, ранее представленные в виде (3) Р_х0(\ 4-НТ） — ЛОР. И затем… ,; м а-г(1 + НТ) — ДТ [х (л + нт）] _ хм х = ИТ-средой JNI— = Лим〜 — — Лим-НФ- /-♦00 /-•00€/-

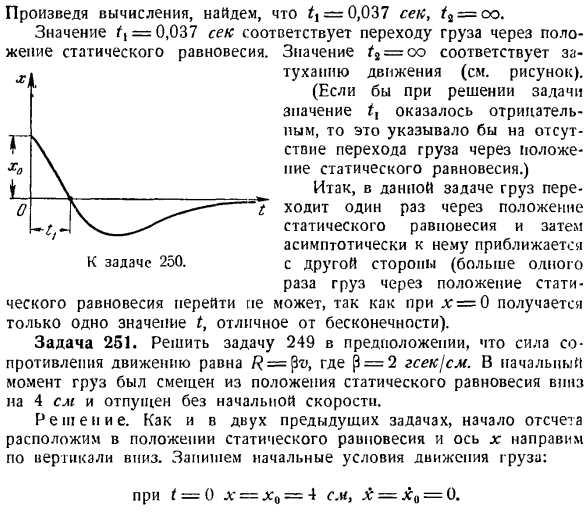
* УО(ПНТ / — 00 не пря ’ Следовательно, Т ОО Итак, согласно формуле (3), груз совершает непериодическое демпфирующее движение. Подставляя числа: i = 10 сек ’ 1,= 4 см, получаем уравнение движения груза x = 4e-l0t(1 + 10/). (4 )） Теперь мы узнаем, проходит ли нагрузка через положение статического equilibrium. To для этого сделайте x в выражении (4) равным маркированному списку.

И значение соответствующего времени, а именно 4r>-’°’（1 + 10 /）= 0.откуда J + 10/, = 0, 0. /.2 = Значение oe соответствует затуханию движения. Поэтому видео существенно отличается от того, что рассматривалось в предыдущем выпуске. При заданных начальных условиях движения нагрузка будет асимптотически близка к положению статического равновесия и не пройдет. Также из-за того, что скорость начальной нагрузки равна нулю, касательная кривой x = ^ x (t) в точке/ = 0 является осью(. 4 Lннколнеколкол-важный момент.

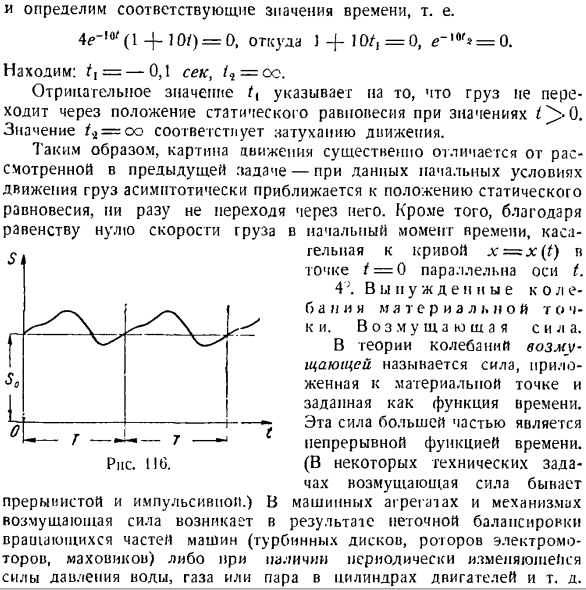
Сила возмущения. В теории колебаний возмущающая сила — это сила, приложенная к точке массы и определяемая как функция времени. Эта сила почти всегда является непрерывной функцией времени. (При некоторых технических неполадках, в результате неправильного баланса вращающихся частей машины (диска турбины, ротора электродвигателя, маховика) или при наличии периодически меняющегося давления воды, газа или пара

в цилиндрах двигателя, возникают механические узлы и возмущающие силы. Она прерывиста и импульсивна.) Происходит заклинивание силы Простейшей является возмущающая сила S, которая изменяется по закону гармонии: sin (pt-8), где// — максимальное значение возмущающей силы(амплитуда силы), p-круговая частота возмущающей силы, 8-начальная фаза. H измеряется в кг, p измеряется, sec’1, b-безразмерная величина. Если сила возмущения S (i)является периодической функцией Второй Период T = т. е. S. (t + T)= S (i) время (рис. 116） Эта функция может быть

расширена в ряд Фурье, если она удовлетворяет условию Дирихле (максимальному и минимальному значениям конечного числа и существованию за период конечного числа точек останова типа 1). Да. С (т)= А0 + 2 Ми, потому что ИПТ-й-БТ грех ИПТ), я = * я Куда? ТТР = 2* -, = \ с 5 (0 соѕ ^ ДТ Би = | ^ С (Т) грех ИПТ ДТ; о б Здесь./ = 0、1、2、3、… Вынужденное колебание материальной точки вызвано действием системы сил, в том числе восстанавливающей силы F и возмущающей силы Pa. В 117 ось Х направлена вдоль линии действия силы F, а точка отсчета принимается в положение

статического равновесия материальной точки. Сила 5 условно направлена вниз, но, как видно из закона ее изменения, ее направление изменчиво. Возмущающая сила изменяется по гармоническому закону: S = Hs ’ n (pt — \ — o).Форма дифференциального уравнения для вынужденного колебания точки масс Л-4 — К * Х = ч греха (пт + б）、 Куда? МММ Pφk p) JC.] закон точки масс в случае 7 задается формулой x = = xl-irx2(где xx-общее решение соответствующего однородного дифференциального уравнения, а n *

9-частное решение неоднородного уравнения). ХХ =cicos, в КТ-л-СЧ грех КТ, хг = грех (Р * + Значение. Л — = С, потому что КТ + С9 грех КТ-л kJl_p. Грех (пт — (-8)). В случае начального условия движения массы, то есть 7 = 0 l:= x0, x = xy, интегральная постоянная выражается формулой: С,= СА =-*>-потому что б. Наконец, уравнение движения материальной точки д — = л * ocos КТ-Ф — * * грех КТ — (3 греха, потому что КТ — (- £cososin КТ Дж −1 ″ к » 1.п * * 1П(Р*+&). Последний член правой части уравнения движения sin (pt — { -&) Принудительная вибрация, определите первое дно термина £ X (\cos

fit-j — * sin kt определяет свободную вибрацию, которую выполняет точка массы, когда нет возмущающей силы. — Т-. * и cos ^ т что б грех Т К—С-Х к; — Флуктуация точки массы, которая имеет свободную частоту и вызвана возмущающей силой L \ Вынужденные колебания материальной точки:= -?Икс Р * * * * р〜 X sin(pt-J-B) имеет круговую частоту P колебаний, равную самой крутой частоте p изменения возмущающей силы (то есть периодичность вынужденного

колебания л ’ 2, вызванного возмущающей силой, равна периодичности этой силы). Амплитуда вынужденного колебания а, то есть максимальная Л Динамическое перемещение массы равно a=^. Статическое перемешивание точек масс под действием постоянной силы H= Я? Динамический коэффициент L-это отношение амплитуды вынужденных колебаний к статическому смещению а//. О. Влияние сопротивления, пропорционального скорости, на свободное колебание точки массы. Когда точки массы движутся в среде, которая блокирует движение (воздух, жидкость), возникает сила

сопротивления движению. Эта сила при низкой скорости точки может быть приблизительно оценена как прямо пропорциональная 1-й степени скорости точки. Р=где P-постоянный коэффициент. Fast-2-я степень скорости точки: R = $ \ V * t, где p-постоянный коэффициент. Ниже мы рассмотрим свободное колебание материальной точки при наличии силы, пропорциональной мощности 1 скорости точки. Р=:$ В. В этом случае форма дифференциального уравнения движения материальной точки икс+

Динамический коэффициент X определяет, является ли максимальное динамическое смещение точки массы, вызванное флуктуирующей возмущающей силой S = Hsin (pt-о), больше / / / статического смещения, возникающего под действием постоянной силы. Коэффициент отстройки z — это отношение круговой частоты p к круговой вибрации материальной точки. Частота его свободной

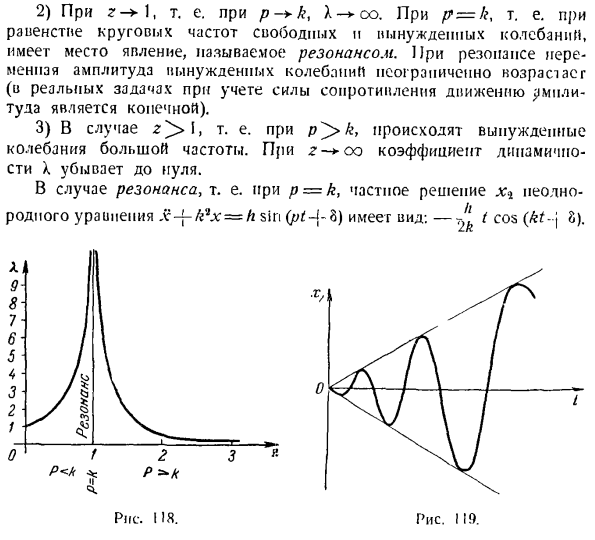
вибрации k, т. е. z = Динамический коэффициент X связан с коэффициентом отстройки z зависимостью X==^.График этой функции показан на рисунке. 118.Рассмотрим его более подробно. 1) Если принудительный IE Низкая частота vibration. In в этом случае динамический коэффициент X увеличивает единицу og бесконечно. 2) для r-I, то есть для p- + k, X—►°°. в случае < p = k>, то есть когда круговые частоты свободных и вынужденных колебаний равны,

явление называется резонансом occurs. At резонанс, переменная амплитуда вынужденного колебания возрастает бесконечно (в реальной материи она конечна, учитывая сопротивление рмили движению). 3) в случае z ^> \ t, то есть в случае r, возникает высокочастотная вынужденная вибрация. для r — * oo динамический коэффициент X сводится к нулю. Для резонанса, то есть для p = k, удельное решение неоднородного уравнения siri, x^, принимает вид:- Jl t cos(kt-j 8). Один. 9-8-7-6- Пять* 3 2 1 111). л 3. * Ф 2 П <А ^ /> = «•* 0.

Рисунок 118. Переменная амплитуда вынужденных колебаний при резонансе д = F увеличивается прямо пропорционально времени(рис. 119). Уравнение движения массы в случае резонанса l. E. формат p = kt имеет вид х = х0 соѕ тыс. т + — к°грех КТ-Джей-потому что б грех КТ — £я, потому что(КЛ-й Б). Л Последний член уравнения равен/ cos (kt-j-Z). £ Требуемая вибрация, первые 2 члена x0 cos kt + — L sin kt Совместимость со свободной вибрацией Если возмущающая

сила отсутствует, то термин cos b sin kt равен Вибрация, вызванная возмущающей силой с круговой частотой свободной вибрации. Фазовый сдвиг между возмущающей силой и вынужденным колебанием материальной точки (рис. 120）： 1) в случае вынужденной вибрации низкой частоты, то есть в случае p <^ k, фазовый сдвиг e между возмущающей силой S и вызванной ею вынужденной вибрацией равен нулю. (Сила возмущения и вынужденное колебание одновременно достигают максимального и минимального значений и превращаются в пулю.） −2) для резонанса, т. е. при р = ку, фазового сдвига между возмущением силы

и вынужденных колебаний XQ является〜(вынужденных колебаний、 Фазовая задержка от этой силы вызвана возмущающей силой Да. / < 1 П <к P> К 3) принудительный случай совместного риса. 120.Высокочастотное качание, то есть Сдвиг фазы между s Возмущающая сила S и вынужденная вибрация jc9 равны z (вынужденная вибрация находится в фазе позади соответствующей

возмущающей силы только tf). Рассмотрим случай, когда сила возмущения S (t) является периодической функцией времени в периодическом T. разложим ее в ряд Фурье. С (т)= з-> А0 4-г(а (Косинус ИПТ + Би греха ИПТ）、 £Ам я• * = я т т т т 2л 2С 2г Здесь р = -т-т \ Аи = потому что ИПТ ДТ, Би = Т — \ Х(Т)Сири Около 6 Здесь./ = 0、1、2、3、… Тогда дифференциальное уравнение для вынужденного колебания точки массы принимает вид И Я + & РТ = 14°с COS Р * + БТ грех. уравнение движения массы при p-f. k выглядит следующим

образом: x = x-2), где общее решение соответствующего однородного дифференциального уравнения является частным решением Неоднородных уравнений： ХВ = сі потому что КТ + С9 грех КТТ СП rn-2 («F ^ Tv C0S ipt + — K ^ F sinipt) — i-1 в начальных условиях вида x = x0, x = x0, t = 0 интегральная константа имеет следующие значения: Г / 1 п0■1 в Адж \ л /> в ^ я-^ 2 С ’Т \ ЛД к-я * Р*)’ 2 к Т У Л К * -Я * П * 0 Наконец, уравнение движения точки массы описывается в виде R. * = Д: 0, потому что Т + А. Син-т — а + JL и г п^) потому что **- -(.？- £.？\

Sin JW4-1 A-L Ж \ К Л к * — ПП ’ / ’ 2 с ’ И + — 5г д(М ^ в COS ^ + л ^ ФСИН• н Вот 2 cos ipt + fe8 ^ V Sin ipt)~ ~ принудительно Важный момент качели. lg0 cos sin kt-свободное колесо Разбивка ключевых точек, которая произошла бы, если бы не было помеховых сил; — (М 1°+!салат ромэн££-»» «» Меня—меня. — Колебания точки масс, которые вызваны возмущающей силой и имеют круговую частоту свободных колебаний; при k = ip генерируется резонансная вибрация порядка i =

l, 2, 3, I-ro. для k = p резонансная вибрация 1-го порядка,£ = 2/7, резонансная вибрация 2-го порядка и т. д. Для одного и того же порядка коэффициентов A /и B/ амплитуда уменьшается по мере увеличения порядка резонансной вибрации. Поэтому в таких случаях наиболее опасной является резонансная вибрация низкого порядка. Если сила возмущения задается тригонометрическим полиномом, то есть отрезанным рядом Фурье с i = n>, то число резонансных колебаний равно n.

Влияние сопротивления, пропорционального скорости, на вынужденное колебание точки массы. Вибрируйте точку материала m под действием восстанавливающей силы F, возмущенной силы S и силы Сопротивление движению пропорционально скорости точки R = — fo, где 8-постоянный коэффициент. ось x направлена вдоль силовых линий F и S (рис.121).Точка отсчета берется в положении статического равновесия материальной точки. Возмущающая сила изменяется в соответствии

с гармоническим законом vS * =Hsin (pi-f-о). Дифференциальное уравнение для вынужденного колебания точки массы при наличии силы сопротивления пропорциональной скорости имеет вид、 х—2) іх-й-КЛК = ч греха (пт-п-о）、 Где: 2 = h = 11 м ’ в * М В этом случае уравнение движения является материальным i’NC. 121.Точки: x = xx-\ — xb, где jc-сумма. Решите соответствующее однородное дифференциальное уравнение. x * — конкретное решение неоднородного дифференциального уравнения. Решение. Vj согласно соотношению n> b、 n = k получается в одном из вышеуказанных

форматов (см. стр. 76-79). Конкретное решение ВР, которая определяет принудительный вибрации、 х} = грех (ПТО-е）、 Куда? ч. 2 пиаром=———、е-arctg,-.: -«. V число-P*) * f 4, lXPs k — ~ ~ ~ p Путем введения обозначения А (ф)= а, грех (пт ы-е）、 г(К-Р*) * 4Н * п * Получим уравнение движения массовой точки в окончательном виде: (С, грех ВК -НП + С, потому что ВКЛ-рил т)+ а (/) для N 0- для Определены

константы интегрирования C и C, но заданы начальные условия движения: f = 0 x = xQt x = x0. 3. во всех случаях n = k и k) когда xx входит, движение X \немедленно исчезнет, но、 х Амплитуда вынужденных колебаний a = Не зависит от основной частоты p и времени вынужденной вибрации sd. «»» Круговая частота P вынужденной вибрации x4 равна возмущающей силе, а круговая частота p-периодической частоте вынужденного колебания R.E. периодическая Γ вынужденной вибрации и возмущающая сила силы

равны о р г. j Вынужденное колебание максимальной частоты nrenedia * МАПО/) чистоту$ < Норовиния Рисунок У2. Различают 3 типа поведения.а) rt <^ k — для низкого сопротивления, б) n ^> k-для высокого сопротивления, в)n = k-для предела. а) n <^ k — для низких resistance. An важным моментом является выполнение затухающих колебаний по закону. * = Ас-НТ грех(] / к *-рил Т +а)(Ф-СХ — * 0). Для начальных условий данного упражнения (f = 0 x = xQ, x = xQ) A и a имеют вид: Это движение не является периодическим, так как Формула Ae-nt переменна и убывает экспоненциально. Однако круговая частота и период колебаний также вводятся здесь по аналогии

со свободной вибрацией. Круговая частота колебаний материальной точки при наличии сопротивления КР = 1 То есть сопротивление движению, пропорциональность Уменьшите скорость, круговую частоту вибрации. Период колебаний точки массы при наличии сопротивления, пропорционального скорости 2 * 2 * Такие колебания. Это означает, что сопротивление движению, пропорциональное начальной силе скорости, не влияет на величину круговой частоты

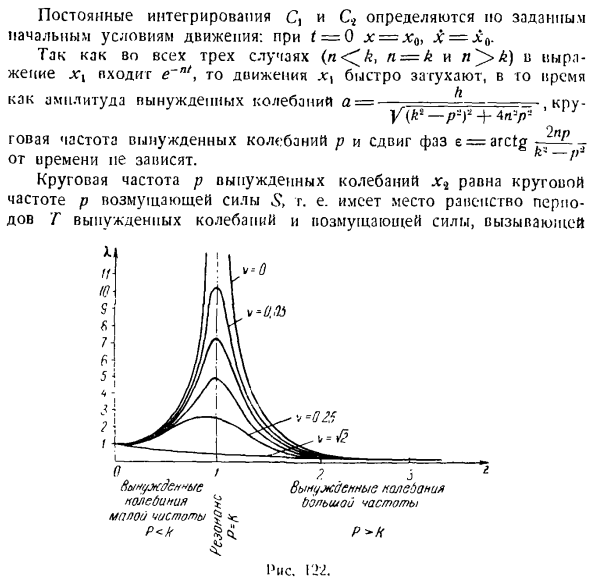
вынужденного колебания точки массы. Переменная амплитуда вынужденных колебаний при отсутствии сопротивления бесконечно возрастает при резонансе. То есть использовать=по закону: a—t. если существует сопротивление, пропорциональное скорости, то амплитуда a постоянна и равна следующим значениям: _ Л В3-2 Зависимость коэффициента X красителя от коэффициента расстраивания z имеет следующий вид(рис. 122): 1р Каждая кривая, показанная на рисунке, соответствует определенному значению v.

С увеличением v, то есть увеличением сопротивления, динамический коэффициент X, а следовательно, и амплитуда вынужденных колебаний уменьшается. В зоне вынужденных колебаний высокой частоты, значительно превышающих резонанс (например, в случае r> 3), практически все кривые сливаются, независимо от величины v. Поэтому в этой зоне при расчете амплитуды вынужденных колебаний можно пренебречь сопротивлением. Максимальный динамический коэффициент х не возникает при резонансе. Он сейчас

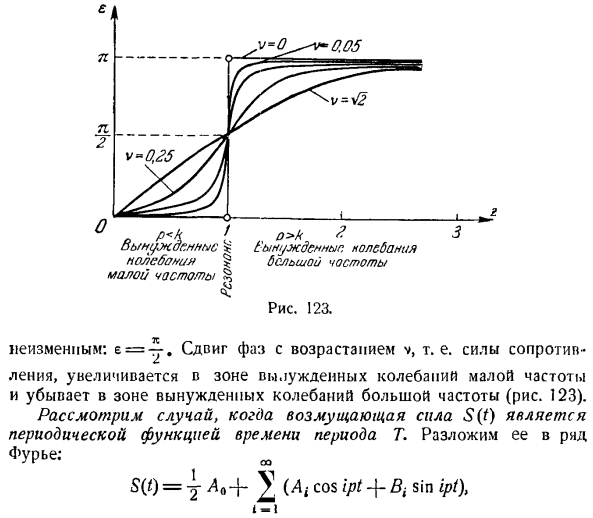
в зоне. = Y 1-2v *. в то же время Lshah- 2В У1-ва VT. Если функция X = / (;’) монотонно убывает. Два Фазовый сдвиг между возмущающей силой и вызванной ею вынужденной вибрацией e = arctan j ^ — j остается резонансным. Без изменений: фазовый сдвиг с увеличением е = v, т. е. сопротивления, увеличивается в зоне вынужденных колебаний низкой частоты, уменьшается в зоне вынужденных колебаний высокой частоты(рис.123). Рассмотрим случай, когда сила возмущения S (t) является периодической функцией времени в периоде 7.Разверните в ряд Фурье. С(т)= yA0 — | — ^ (^я, потому что грех ИПТ）、 Я…

Куда? т т т т АИ = Дж ^ С (Т), потому что iptdt,= 5(0 грех ИПТ ДТ \ Здесь я= 0、1、2、3、… В этом случае дифференциальное уравнение вынужденного колебания материальной точки при наличии силы сопротивления, пропорциональной скорости, имеет вид、 Ноль ноль X +2пх + k * X = — J + −2 (л, I COS IPT + BT Sin IPT). Тогда уравнение движения точки массы выглядит так: x = X \ — \ — J-x2.Где xx-общее решение соответствующего однородного дифференциального уравнения. Х2-это конкретное решение неоднородного

дифференциального уравнения. Колебания во всех 3 случаях xx: N <^ ky N = k, N ^> K затухание (см. стр. 76-79). Вынужденные колебания, которые определяются конкретным решением xb, происходят по закону. И = + 2 потому что пли + Би греха ИПТ) л I = 1 Куда? _ 1 и AJ(к *〜я в -)-2ntp Ай-м(К2-я-Р’) * 4-4Н * я * Р *’ _ 1 Лю ^ — р-п ^ + lsipai м(К2-i2p2)—{-4Н * я * Р * ’ при k = ip резонансная вибрация 1-го порядка occurs. At в то же время __ =- 1 т ы прес ’ 1 т 2inp ’ Решение задачи вынужденного колебания массы рекомендуется в следующем

порядке: 1) Выберите точку отсчета и возьмите начало координат в положение статического равновесия точки массы. 2) Запишите начальные условия движения точки масс. 3) нарисуйте на рисунке силу, приложенную к важным точкам. 4) Создайте дифференциальные уравнения движения в проекции на соответствующую ось. 5) интегрируйте дифференциальные уравнения движения, используя начальные условия для определения интегральной постоянной. Предположим, что все важные точки

нарисованы в среднем положении, соответствующем их положительным координатам, и точка движется в направлении, где координаты увеличиваются. При составлении дифференциальных уравнений движения необходимо использовать статические равновесные состояния важных точек. Это часто разрушает многие постоянные члены в правой части дифференциального уравнения движения. Если скомпилированное дифференциальное уравнение идентично любому из приведенных выше уравнений, вы можете

использовать приведенную выше формулу для получения результата немедленно, даже без интегрирования этого уравнения. При решении задачи в общем виде необходимо определить численное значение коэффициентов дифференциальных уравнений. Поскольку форма частного решения уравнения зависит от круговых частотных соотношений вынужденных и свободных колебаний, то есть от Р и К. Именно поэтому необходимо интегрировать дифференциальное уравнение движения f1x — = H sin (pt -} −8). А) если резонанса нет, т. е. p ^ k, то частичное решение xq будет записано в виде= a sin (pt-j-8) — j-cos(pt-J-o) (очевидно,£ = 0 ）; 6) найти конкретное решение Xi

в виде=£, x *при наличии резонанса= sin(pta) fit cos (pt + b). Интеграл дифференциального уравнения движения X — {- 2пх-}- K * x = h s \ n (pt-’rb)> независимо от соотношения между p и k, необходимо искать конкретное решение chl в виде: ХВ = грех (пт-(- б)-ф-Б Кос(пт + б） При решении задачи, в которой необходимо определить условия, обеспечивающие попадание массы в резонанс, дифференциальные уравнения движения не должны быть integrated. To для этого

достаточно с помощью составленных дифференциальных уравнений движения определить круговые частоты свободных и вынужденных колебаний и уравнять их между собой. Задача 252.На этом рисунке показана схема устройства для измерения давления. Стрелка P прикреплена к ползунку A с весом P = = 196 г и отмечает отображение фиксированной шкалы C. ползунок A, прикрепленный к краю пружины O, перемещается по идеально гладкой горизонтальной поверхности. Горизонтальная сила 5 = Hs \ npt была приложена к ползунку. Где:/ / = 1.6 kg> p = ($0 sec ’ 1.Модуль упругости пружины равен f = 2 кг / cm. At в первый момент ползунок находится в состоянии статического равновесия. Определение: уравнение

движения стрелки B, коэффициент динамичности, коэффициент расстраивания при отсутствии сопротивления. Уравнение движения стрелки H при наличии силы сопротивления, пропорциональной первой степени скорости ползуна:£> =(to, где p = 25,6 кг-сек / см. Решение. направьте ось x горизонтально вправо, параллельно оси пружины, и возьмите точку отсчета в положении ползуна, соответствующем деформированной пружине. Начальными

условиями для движения ползунка являются: t-i) как x-0, x = 0 Рисует смешанный ползунок справа от x от равновесия position. In в этом случае пружина равна A = l \ И К выпуску 252. Следующая сила приложена к ползунку. P-собачка ползуна, N-вертикальная реактивная сила горизонтальной плоскости, сила F-упругая сила пружины растяжения, ее выступ находится на оси.Рания создайте

дифференциальное уравнение для движения ползунка в проекции на ось X. ТХ = ЗХ-Ф стан fxj Или ИФГ. 。Пример х = грех пт — — — ° — х、 Откуда? Я + к * х = ч греха Пти（]） Где: k = y, h =—. в этом случае k = 100 cetrl9 / 2 = = 8000 см-сек — ’ 1. Уравнение (l) является линейным неоднородным двумерным дифференциальным уравнением с постоянным коэффициентом.

Общее решение уравнения равно сумме jc-общему решению соответствующего однородного уравнения x + k * x = 0(2） А x ^ — конкретное решение выражения (1), т. е. Х = Х \ — Х.2. (3） Построить характеристическое уравнение:= 0, откуда Р / 9 =это волнует. Так… Х \ = С, потому что КТ-Джей-Ка грех КТ. (4 )） Чтобы определить вынужденное колебание, то есть конкретное решение Xb, необходимо сначала найти соотношение между круговыми частотами свободных и вынужденных колебаний. Если 6 = 100 секунд\и p = 60 секунд -\, то p <^ kt, то есть вынужденное колебание низкой частоты occurs. In кроме

того, конкретное решение должно быть найдено в виде: xh = a sin pt-j-V cos pt, (5） Где A и B-коэффициенты, подлежащие определению. если подставить x2 в дифференциальное уравнение(1) и уравнять коэффициенты в левой и правой частях уравнения для соответствующей тригонометрической функции, то получим: Так… Конкретное решение, описанное в Формуле (5), имеет вид: То есть, D так, сила сопротивления пропорциональна скорости、 Увеличьте период колебаний. Как правило, переменная амплитуда колебаний a

= Ae-nt является по существу максимальным отклонением, которое было условно введено. Амплитуда колебаний a = Ae-nr(* oo a-0) л7 х. Потому что нет никакого сопротивления, т. И затем… 7> = г Г ’ — (я)’ Используйте Формулы (4) и (b), чтобы написать общее решение в соответствии с формулой (3). х = С {потому что КТ С2 грех КТ-Джей-грех пт. (7 )） Чтобы определить интегральные константы C и C2, вычислите: Λ= — Cxk sin ki + C . Он Ы & ы = ы -С = К ™с грехом пт-ПТ и грех. если вы используете hc = c — = Hk, это выглядит так: м О вышесказанном*•、 БТ лни греха пт к * п * Относительная погрешность прибора составляет AS /> 2 Г-С ’ — ’ В-П * * Относительная

погрешность прибора незначительна в случае»I» 0.Это происходит в случае K;> p. если k = / / ^、 Сделан вывод о необходимости установки пружин с высоким коэффициентом жесткости. Чтобы найти значение динамического коэффициента X, используйте формулу X = a/D//. a = 1,25 см и D / / = H; c = 1,6 / 2 = 0,8 см, поэтому l = 1,56.Это означает, что амплитуда вынужденного колебания более чем в 1,5 раза превышает статическое смещение. Соответствующее значение коэффициента

расстраивания 2 равно r = /> /£= 60/100 = 0.6. Эта задача решается с учетом сопротивления движению R = 3r>.£ 25,6 кг <сек j см, v-скорость ползуна a. Сопротивление движению / силе, ранее добавленной к слайдеру? Он направлен в направлении, противоположном скорости движения. Предполагая, что ползунок A движется в направлении абсциссы L*, которая увеличивается, он будет указывать силу#, но горизонтально влево («лед кабриолет =

Зх + Форекс + ГХ Или На. 。 3jo-.се * = > см пт-исправить — ^ х、 Откуда? х — {- 2nx-\ — КЛК = ч греха Пт(10） Куда? к = 1=! 00 s — \ » = = h = — * = S000 см / с *、 Р = 60 секунд 1. Следовательно, это n <^ k и p <^ k. Общее решение дифференциального уравнения(10) имеет грабли. (И） Х \ — общее решение соответствующего однородного уравнения £ — )- Ittx -} — k * x = 0, (12） Xb-конкретное решение неоднородного уравнения. (12) соответствующая форма характеристического уравнения имеет вид R9-J-2nr kl = 0, из которого r = — n:±Yrv — / A n Т) (13

если вычислить xb xb и заменить их на XJ в дифференциальном уравнении(10), то коэффициенты на правой и правой сторонах уравнения будут равны синусу и Косинусу: А (к -п) — Wnp = ХТ Ч(к * — п*) — Джей-2Apr = 0 После решения этой системы уравнений определим: 4 _ _ _ футов (фут-р’) р_ _ 2nph_ _ П(к * .- п*) * + 4Н * п * 9 (Ст3 Р *} + 4Н * п * А если ввести значения A и I в Формулу (14),

то получим: Л(СТ4-ПС). Инф. / 1СЧ = «7 — ^ ’У-Син Ф ^—ТТ^ — -:-п-потому что тг о/.(1 5） (ФТ-п -)-в-п-р (к-п-г — 7 в-р — ^ в ’ Здесь, используя формулы (13) и (15), можно обобщить дифференциальное уравнение (10) в виде: х = р — „(С, стоимость-г С2 грех / я (футов * — О2). 2л /?//, / Вт. в * ■- Фут) з ы, н пт — (к— ^ ^ Потому что ПТ 0） Чтобы определить интегральные константы C и C1r, вычислите: n — = — ne-n ((c, cos | -Ф Е Н ((- С, грех В Л * — Я * * с * соѕ ^ / р—л * т) — ф- 。 л. с. (К-П -). 。 2lr -/?

。 。 17 часов Если подставить уравнения (16)^ = 0, d:= 0, а уравнения (17) T = 0, l * = 0, то получим систему уравнений. o_g 〜 — Р11 — АП 01(КС-р + г + * п? ’ о = — “ С+ с+ (Л — / Р’) * — Ф 4Н> < ’ откуда * _ _ 2nph _ _ _ л. с. (К-П *〜 ’> Н’） (k * + Ln’P — > ^ \ {b * — pG — + 4 * T> 3] Vv ^ 7 * ’ Если вы присвоите E1I значениям C1 и C1 в уравнении (16), то найдете нужную формулу для перемещения ползунка A, а значит и стрелки 8. х =(Frfey (2ncos нет.-1 + ’УР-Н**’ Вводится следующая нотация. РН (2l9-

Ф Н2-/ Р2) 2nph. —— ^г,= ^ зта,-Р-РТ—, в,;. Р — = б потому что И затем интернет (к’— Р2）_ Уравнение (18) принимает вид: ДК = БК-НТ грех(Дж / ^ ’4′ — т + а) — ф грех(ПФ-е), (19） Здесь._ РН ГЛЛ л я（ <•+ /> -» 2л (Л-+ 4 / 12Р _ х ^ нас = ags1a2ya к **-я [ / ™. К *-Н2 ′ А — + Л- ’ 2пr А= -, Е = arctg ^(А * — П*) * 4-4Н * Р * 9 К * — П для цифры π= 64 сек’1, РР= 100 сек 11, р = д0 selg1, ч = 8000 см / сек*,£ = 0,63 см, а = 1.74 рода, а = 0, 8 см, з = 0.87 / сек. Таким образом, уравнения движения ползунков A и B будут иметь вид: x = 0.63 Первый член уравнения (20) определяет колебание стрелки с частотой свободных колебаний.Свободное колебание быстро ослабляется наличием фактора e-W. 2-й член формулы (20) определяет вынужденное колебание стрелки В.

Уравнения (9) и (20) 2-го слагаемых определяют соответственно вынужденные колебания стрелки B при отсутствии и отсутствии сопротивления движению.Из сравнения полученных результатов видно, что сопротивление движению не влияет на круговую частоту вынужденных колебаний.Как в уравнении (9), так и в уравнении (20)^ = 60 сек1;амплитуда вынужденных колебаний при сопротивлении

уменьшается. Она уменьшилась с 1,25 см до 0,8 см, а сопротивление движению вызвало фазовый сдвиг между возмущенной силой и вынужденной вибрацией. Задача 253.Определите уравнение вынужденной вибрации стрелки устройства, описанного в.Предыдущая задача, если сила возмущения S изменяется в соответствии с уравнением S = / is ‘\ upf, где/ / = 1,6 кг, p = 100 с » 1.Если нет сопротивления движению, если есть сила сопротивления движению # =где Р = 25,6 кг-сек / см, где v-скорость ползуна а со стрелкой В. Решение.Используйте дифференциальное уравнение (1) предыдущей задачи. х + к * х = ч греха пт(я） Здесь._ _ i / » 2000 * ухо<.ЛЛ、 к = г = г-з — = 100 cevr> П = 10 С-1 。 ifg [600-t SLPL И= = — rr ^ — = 8000 cm•sm; и 1UC Как это сделать? = £ =. 100 деревня; » 1-й, есть

явление резонанса. Для резонанса при p = k конкретное решение дифференциального уравнения(1) должно быть найдено в следующем виде: Х2 = грех в пт-Джей-Би, потому что ПТ (Д） Для определения коэффициентов A и B используйте формулу (I) x. подставьте g. To сделайте это, вычислите следующее: х ^ = грех, пт-Ф-Апт потому что ПТ 4-в COS пт-Б, пт греха пт= 2 ап, потому что ПТ пт-Ар1 греха пт-2bp по грехом пт-ДГПЖ, потому что ПТ. Коэффициенты левой и правой частей уравнения (1) равны синусу и Косинусу, и, используя p = k,

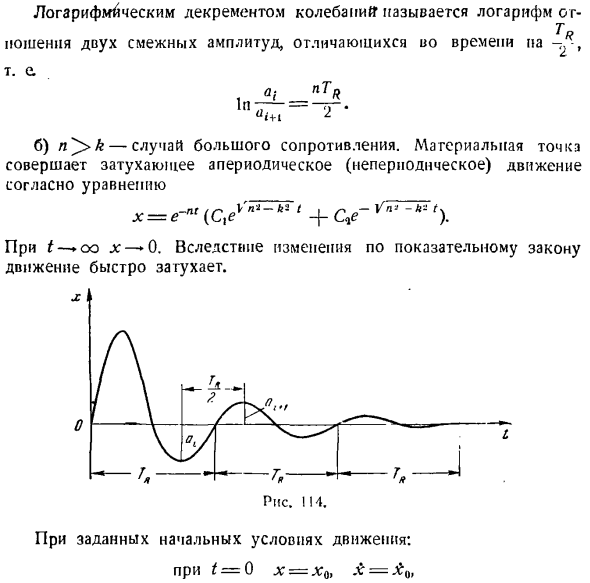
получаем-2Bp = ^ h. 2 Ar = 0. Когда мы решаем эту систему уравнений, мы получаем: х Логарифмическое уменьшение колебаний называется логарифмом TR. Несет 2 смежных амплитуд, отличающихся по времени Деньги. −2 Р В b) n ^> k-это случай высокого сопротивления. Масса совершает затухающее непериодическое (непериодическое) движение согласно уравнению. в Н *-К2 Т x = e-ntlctea’a — «’ 1 + ОО, как Джей-Си-0.Из-за изменения закона индекса движение быстро затухает. Для начальных условий данного упражнения: t = 0 x = l; 0, x = J?0.、

Здесь формула (G), определяющая вынужденное колебание стрелки B, принимает вид: Х <1 = — потому что ПТ. Если вы вычислите число и введете фазовый сдвиг, вы увидите следующее: = 40 / sin (см. 100 * — \ j (2) Переменная амплитуда вынужденных колебаний при резонансе i i = 40 г! разбег cm прямо пропорционален времени, поэтому он угрожает безопасности машины, на которой установлено устройство и прибор (на самом деле уравнение вынужденной

вибрации отличается, так как оно устойчиво, по крайней мере, к нескольким движениям).См. 2-е решение проблемы). Круговая частота вынужденной вибрации равна круговой частоте возмущающей силы: / 7 = 100 секунд вынужденная вибрация отстает Но фаза от возмущающей силы при Y. Если учесть сопротивление движению, рассмотрим этот вопрос=где Р = 25,6 кг-сек / см В этом случае можно воспользоваться дифференциальным

уравнением (10) предыдущей задачи. * — Джей-bxxp & х = ч греха ПТ (3） Куда? // = 6 = 100 секунд\ / 1 = ^ = 64 секунды — \ / = 8000см-СС〜\ Чтобы найти вынужденную вибрацию стрелки на приборе, ищите частые решения следующего вида x., = a sin pt + B cos pt. (4 )） Чтобы определить A и B, вычислите x ^и N \ 2. ХВ = ап, потому что ПТ-ВР грех ст; СН. г = — Ар1 греха пт-ВР * сов пт. Подставляя эти значения в уравнение(3) и приравнивая коэффициенты левой и правой частей

уравнения к синусу и Косинусу, получаем: Λ (**- p2) −2 =Λ; в (k * — p1) — r 2.4 pr-0 Когда мы решаем эту систему уравнений, мы получаем: 。 ч(В-П -)__ 2nph_ Эти. Присвоение выражению(4) значений 4 и B дает h(k * — p -). в 2 НПХ Введем обозначение для определения амплитуды а и сдвига фазы g между вынужденными колебаниями и возмущающими силонами. ч(К2-п -) Inph Уравнение(5) принимает вид: ХІ = грех (пт-э), (7） / de fl и e определяются из системы

уравнений(6). //. 2пr А = —с = arctg- к— ■ п В данном случае, резонанс П = К. таким образом, а = т, е = 0, и выражение (7) примет форму: Для чисел:= 8000 см-сек » а, находим： I = 64 секунды ’ 1, p = 100 секунд-19/1 = x * = 0,625 sin (100/ -) см Из сравнения формул (2) и (8) видно, что при отсутствии сопротивления переменная амплитуда вынужденного колебания стрелки В при резонансе увеличивается прямо пропорционально времени: а = 40т см, при наличии сопротивления

движению R = 25,6 Т; кг, амплитуда составляет постоянную величину, равную 0,625 см. Величина окружной частоты и фазовый сдвиг вынужденного колебания не влияют на сопротивление при резонансе. Задача 254.To регистрируют вибрацию подвижного состава, подвешивают пружину к потолку транспортного средства, коэффициент ее жесткости равен с = 10 г-см. Конец пружины нагружен грузом весом стрелки B P = 98 г (см. рисунок).При

вертикальной вибрации автомобиля, то есть в точке А, начнется вибрация груза! Это записывается путем перемещения стрелки вдоль шкалы, которая отображается на стене автомобиля. Деформация-это формула 5 =/?При колебании согласно, напишите уравнение движения стрелки B и определите динамизм и факторы расстраивания. грех/;/, а = 0,5 см, КРН-1. В первый момент нагрузка была неподвижной в положении статического равновесия. Игнорировать сопротивление нагрузки. (8） Цель 254. Движение Определение: позвольте мне ввести ось x, связанную со стационарной средой. Опорная точка выбирается в положении статического равновесия нагрузки. ось X ориентирована вертикально вниз.

Обратите внимание на начальные условия движения груза, обращаясь к неподвижной оси X. Для 1 = 0, x = x = 0, x = xz = 0 Покажем груз промежуточного положения, смещенный вниз от опорной точки x. когда каретка неподвижна, в этом положении груза пружина будет растягиваться только на Dst x. однако в вагоне происходит сдвиг, и в результате происходит сдвиг в точке A pa. Поэтому

удлинение пружины D лишь немного, то есть= = летнее время 2 усилия приложены к нагрузке. Его масса P, а также упругая сила F пружины, которая выводится в связи с удлинением пружины, действуют вертикально вверх、 создайте дифференциальное уравнение mx = P + Fx для движения груза в проекции на ось X. Учитывая выражение (I), мы пишем: МХ = Р-cDst-СХ — \ — с \ В положении статического равновесия * = ξ= 0, P-c ^ ct = 0 дифференциальное уравнение движения имеет вид Техас — СХ + КБ. Условие 1 =грех по pt. So … МЮ£- \ — СХ = СА греха пт. (2） Получено дифференциальное уравнение вынужденной вибрации груза при наличии возмущающей силы cas \ npt = rt. Таким образом, получает

ся, что вибрация автомобиля, а значит и точка А увеличения веса пружины, является причиной возмущающей силы, оказываемой на груз. Перепишите дифференциальное уравнение (2) в следующем виде Х — \ — к * х = ч греха ПТ (3） Куда? k = = 10 секунд ’ / 7 = 1 btg ssk — \ h = syr = 50 см-сек -’ \ поскольку это p ^> k, возникает вынужденное колебание высокой частоты. Если проинтегрировать дифференциальное уравнение (3), то получится уравнение движения груза по неподвижной оси x, которая не связана с автомобилем. x = xx-xx, где xx-вибрация нагрузки, которая определяется общим решением соответствующего однородного уравнения x + kqx = 0, (4）

а-вынужденная вибрация нагрузки, которая определяется конкретным решением дифференциального уравнения(3); решая уравнение(4), можно видеть: ХХ = С \ потому что КТ — [- м грех КТ. (5） Конкретные решения из-за отсутствия резонанса являются、 = Грех пт Б, потому что Пти(6） Где A и B подлежат последующим решениям. После того, как вы рассчитали Xb, в уравнении (3) x * xb X. подставим r. тогда, если мы уравняем левый и правый коэффициенты уравнения (3) с синусом и Косинусом、 Таким образом, выражение (b) принимает вид: Запишите общее решение дифференциального

уравнения (3): n * = rjc, — [- с формулами (5) и (7)、 х = С, потому что КТ С2 грех КТ-Джей-грех пт. (8） CJ и С. Определить 2, рассчитать следующие: х = — С \ к греху КТ — [- дь, потому что КТ +, потому что ПТ. (9） Р п Выражение (8)/ = 0,. Присвойте ему значение ^ =Π0= 0 и присвойте его формуле (9) t = 0, x = x0 = 0, и определите следующее: Г _ _ н _ _ _ р Уравнение движения стрелки принимает вид * = — Pk sin kt + sin pt(при использовании L числовых данных это выглядит так: l:=(0.1 sin 10 / −0.02 sin 16*/) (см. 11) Первые члены уравнений(10) и (II) определяют вибрацию груза со стрелками свободной частоты, а вторые-вынужденную вибрацию. Когда сопротивление

пропорционально скорости нагрузки, вибрация свободной частоты будет быстро затухать. Поэтому в дальнейшем мы будем рассматривать только вынужденную вибрацию груза со стрелкой. * «=Srrjr * в п * ’ Шкала, регистрирующая вибрацию стрелки, прибита к стенке каретки и поэтому вибрирует вместе с кареткой, поэтому стрелка указывает на изменение нагрузки относительно каретки, разность l2, то есть x2 = x2.- ч-Ак *-^ АР — * — Р1 П. С. ч = — и вы увидите следующее: / л Грех (Этот результат можно получить, украв важный

момент относительной динамики движения. См. выпуск 259 в следующем разделе.） Устройство предназначено для регистрации вибраций автомобиля. То есть стрелка указывает на хг. дробь _ s была близка к единичной. Это делается с помощью k. * P〜_ k = » если это устройство должно быть выбрано Очень слабая пружина с с низким коэффициентом упругости. (Чем слабее пружина, тем меньше реакция нагрузки на колебания точки подвеса пружины, так что она неподвижна против колеблющегося автомобиля.)И рассматриваемый вопрос 1.04. Вертикальный сейсмограф (прибор для

регистрации землетрясений) построен аналогично этому прибору. Чтобы найти значение динамического коэффициента X, используйте формулу a = x = 0.04, где a = 0.02 см и & ff = 0.5 см. Это означает, что амплитуда вынужденных колебаний меньше в 25 раз статического перемешивания. Соответствующее значение коэффициента отстройки z 10 до 5LMv Форма интегральной постоянной равна: _ +(n 4 — / ^ CTfcS)^ _ + ft 5）* » ？ 1 2 V ^ ** Иначе говоря — +(н-в ^ — ё)^-«}

Или Х = ^ [(н » 0 4-ПХ П) Ш / Н *-К * т + п0 / Н * — *  ль/]. Характер движения зависит от начальных условий. Когда= x = n’O> 0, то есть материальная точка в первый момент Форма интегральной постоянной равна: _ +(n 4 — / ^ CTfcS)^ + ft 5） » ？ 1 2 V ^ ** Иначе говоря — +(н-в ^ — ё)^-«} Или Х = ^ [(н » 0 4-ПХ П) Ш / Н *-К * т + п0 / Н * — * * ль/]. Характер движения зависит от начальных условий. Когда= x = n’O> 0, то есть материальная точка в первый момент Левый конец

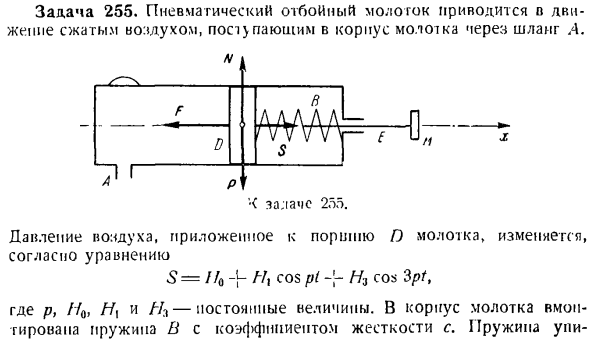
превращается в поршень, а правый — в корпус молотка. Поршень Д подключен к нападающим на прут Е. записать уравнение вынужденных колебаний поршня, когда молоток находится в режиме ожидания. Стержень F, ударник m, масса пружины и сопротивление движению не учитываются. Решение. Возьмем точку отсчета, находящуюся в положении статического равновесия поршня под действием силы / V0 и упругой пружинной силы Fcx, с осью l:

горизонтально направленной вправо. В этом положении пружина сжимается только силой Dst, в этом случае создается упругая сила пружины FCJ = c \ CT. Обе силы направлены горизонтально:/ / 0-вправо, а FCT-влево. запишите равновесное состояние поршня в проекции на ось X. ЯО-сдст =0.(Я） Обозначим поршень, смещенный от нуля вправо x. In в этом случае пружина будет сжата&x =&<r — \ x,

а упругая сила F, создаваемая Pei, будет горизонтально бледно-желтой. его проекция на ось x равна Гонка FX = — с \ х = — с(ДСТ + ЛГ). (2） Кроме того, к поршню прикладывается следующая сила. P-его вес, N-нормальная реактивная сила корпуса, 5-давление сжатого воздуха. создает дифференциальное уравнение для движения поршня D, спроецированного на ось X. МХ = Зх + Fjr

Даны Формула (2) и закон изменения заданной силы S, p -х = х0 ч \ потому что ПТ + / Ул cos3/; / — cDst-экс. С учетом Формулы (1) запишем дифференциальное уравнение вынужденного колебания поршня в виде: х KLX = хй, потому что ПТ -} — потому что 3ptt(3） Куда? * 〜м-п «» я — «ИД — ^ Р. Для определения закона вынужденных колебаний поршня необходимо найти конкретное решение Формулы (3).Рассматривая правую часть этого уравнения, найдите конкретное решение x в виде: (4 )） ХЧ-Ай греха пт-Джей-Би, потому что

ПТ А3 грех 3 ПТ — п-вл, потому что 3 ПТ、 Где y4i, B1> и Bb-постоянные коэффициенты, подлежащие определению. AX) чтобы найти Bb и B3, вычислите следующее: Х. Я = АИП потому что ПТ-Бип греха пт-r3рАлcos 3 ПТ-3 ПТ УДВП ^ Грех,-Грех aip1 ПТ-Б} ЛП, потому что ПТ-9л3р грех 3 /; /-потому что подставив xl x±в дифференциальное уравнение(3) и сравнив коэффициенты в левой и правой частях

уравнения с синусом и Косинусом: А (к * — Р1)= 0,Б {(а * -Р1)= а(к * — г)= 0、 Вот что решила эта система уравнений: Подставляя значения a \ t B,, A3 в Формулу(4), находим искомую формулу для вынужденной вибрации поршня. = Ф ^ Ф1: 05 пт + соѕ 3 ПТ- если k = p, то возникает резонансная вибрация 1-го порядка. Случае? = 3p, возникает резонансная вибрация 3-го порядка. k = j / »» ^ — таким образом, выбор модуля упругости пружины равен Необходимо сделать так, чтобы

неравенства k — ^ bp и K 3p были satisfied. In в этом случае поршень не будет резонировать. Проблема 256.Нагрузка на груз P подвешивается на конце пружины, где коэффициент жесткости равен r. к нагрузке прикладывается возмущающая сила S = f (l). Примените любой метод постоянной вариации и найдите уравнение движения груза. Ось l * направлена вдоль оси пружины, а точка отсчета берется в положение статического равновесия нагрузки. 11 малых нагрузках ： Если I = 0, то X-Xq, X = Xq. Игнорируйте сопротивление движению. Solution. In в положении статического равновесия груза, под действием его веса Р, пружина оттягивается только вниз Dst. In в этом случае восходящая упругая

сила FC1 возникает вертикально, а Fcl = rA(1. (0 П-с \ = 0. Обозначим смешанный груз снизу zero. In в этом случае пружина растягивается только kx = Ast ^ — Lg, а сила упругости пружины F направлена вертикально вверх. проекция на ось X Форекс = — т = — с(ДСТ+*). (2） В дополнение к силе F к нагрузке прилагаются следующие силы: P-нагрузка, S-возмущающая сила, а ее проекция на ось Лапласа x равна Sx = /(i). создает дифференциальное уравнение для движения груза в проекции на ось X. МХ = Р + Зх + Форекс. Для Sx = f (t) и значения

Fx>записываются в выражение (2): х = р -)-/( / )-cDst-СХ. С учетом Формулы (1) запишем дифференциальное уравнение вынужденной вибрации груза в следующем виде: Йк + к * Х = |- /(0, (3） Икс Здесь & =выдать 250. Общее решение уравнения(3) имеет вид x = x {-\ xb. Вот общее решение соответствующего однородного уравнения. Си = Сиджея, потому что КТ С2 грех КТ, (4） x ^ — конкретное решение неоднородного уравнения. Однако в любом законе изменения силы возмущения= = / ( / ) нахождение конкретного решения

дифференциального уравнения (3) по выбору часто сопряжено с большими трудностями. Для решения этой задачи мы применяем любой метод постоянной вариации. Ищем решение уравнения (3) вида: x = Q cos kt-j-C <I sin kt, (4-й） Это похоже на общее решение однородного уравнения. Однако мы считаем, что С1 и С2 являются функциями времени и подлежат последующим решениям. Поскольку мы ввели 2 функции вместо 1 неизвестной функции, мы имеем право наложить дополнительные условия на Q и C-2.Используйте формулу

(4), Чтобы вычислить x заранее. Что взять： х = — С \ к греху, к-Т 4-С%К, потому что КТ С | потому что КТ Си, грех КТ. (5） В качестве дополнительного условия упрощения расчета возьмем следующее. Ки, потому что КТ-Ф С2 грех Кт = 0. Тогда выражение (5) принимает вид: х = — С, к греху КТ-Ф-ЦИК, потому что Т тыс. после определения x вычислите следующее: £=- я * — дь * количество-грех, грех КТ-Ф С ^ К, потому что КТ. (7 )） Подставляя q из уравнения (4a) и уравнения (7) в дифференциальное уравнение (3), получаем 2-е отношение, связывающее функцию C|.И С2： (8） -С, грех КТ — П-С * К, потому что

* =£ф(т). 「• Решим системы (6) и (8) относительно C’I и Cr, C,= — * / ( / ) sin kt, Ca = r | /(0 cos A /、 (6） Откуда О О Подставляя эти значения функций Ci и C2 в уравнение(4), получаем: т. = С, потому что КТ + Qsin-т-а-т ^ /(х) грех к-Ди-младший о. т. грех т ^ /(т), потому что к-д〜、 Привет. Я… х = С, потому что КТ—§ру * грех КТ -\ -^ ^ /(?ФЛК (т-т) 9） Ноль Чтобы определить интегральные константы C и C2, вычислите: т. х = — дь грех КТ + С. 2К, потому что-1-££/（-:) cosЛ (Т-Т) (10） Ноль (9) присвоить:/ = 0, x = xQ. И o (10) t = 0, n » = n0、

Вводя значения интегральных констант C {и C2 в уравнение (9), получаем уравнения, необходимые для движения груза. т. х = ДУУ потому что КТ-дж-дж грех КТ-ч ^ ^ /(т) грех — (11） О Первые 2 члена формулы (11): xQ cos kt-j-sin определяют свободную вибрацию нагрузки, выполняемую при отсутствии возмущающей силы S-/(t). г. Последний член формулы (11) — ^ / ^® sin k (t — ^ rft op Ноль Вибрация

груза делится на свободную частоту, вызванную возмущающей силой, и вынужденное перемещение груза под действием возмущающей силы S = /(t). Уравнение (11) может быть широко использовано при решении задачи динамики произвольных законов флуктуаций возмущающей силы S — = f (t) и вынужденных колебаний точки mass. As уже указывалось, что его рекомендуется использовать в тех случаях, когда трудно найти конкретное решение дифференциального уравнения З + КЛК = jjf по(Т).

Смотрите также:

Предмет теоретическая механика

Определение сил по заданному движению	Относительное движение
Определение движения по заданным силам	Дифференциальные уравнения движения системы материальных точек