Колебания жидкости в прямоугольном сосуде и в круговом цилиндре

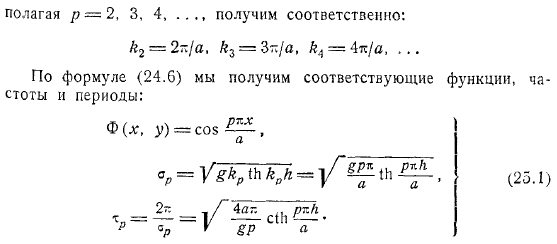
Колебания жидкости в прямоугольном сосуде и в круговом цилиндре

Обратимся к случаю особого хода гидромеханики. Получаем следующие потенциальные потенциалы из формулы. Таким образом упростить уравнение. Выполняется в случаях. Во-вторых, может быть где-произвольное целое число.

Таким образом колебания тяжелой жидкости в сосуде , можно рассматривать движение жидкости, заключенной в прямоугольный контейнер любой ширины. Длина этого контейнера должна быть кратной. Давайте дадим прямоугольный контейнер длины и ширины. Затем, из условия Тебе решать.

• Предположим, вы хотите получить. Предположим, вы получите его соответственно. Уравнение дает соответствующую функцию, частоту и период.
• Если жидкость бесконечно глубокая, она выглядит так. И наоборот, если глубина жидкости мала по сравнению с длиной.

Уравнение показывает, что свободная поверхность является косинусом с полуволной. Людмила Фирмаль

Показан узел вертикального перемещения, построенный для данного случая. Последнее определяется по формуле. В нашем случае это уравнение принимает вид.

Существуют следующие решения. Следовательно. Форма может колебаться узел. Так, в прямоугольных бассейнах разных эпох. Однако последнее определяется весьма специфическим образом. Это также верно и в других случаях.

• Чтобы получить более общий случай вибрации. Это сводится к тому, что ось будет не перпендикулярна к волновым панелям, а прямая линия, которая будет составлять ось и угол.
• Симметричное относительно оси движение определяется функцией. Линейность основного уравнения позволяет сформировать следующие решения.

Это означает простоту. Уравнение оптимизации является легко интегрируется. Обратите внимание только на конкретные решения ниже. Таким образом, можно возвести стену, на которой уравнение задается формулой, не нарушая движения жидкости.

Давайте дадим прямоугольный контейнер. Людмила Фирмаль

Для простоты жидкость бесконечно глубока. Определяет частоту и длительность возможных флуктуаций в формуле (любое неотрицательное целое число). Если глубина жидкости мала. Указывается линия уровня поверхности корпуса.

Узловая линия — это линия, показанная на чертеже, параллельная осям. Чтобы проанализировать случай цилиндра, мы вместо этого вводим полярный. Основное уравнение принимает вид Самостоятельно найти решение этого уравнения. Вводим новую переменную для определения полученного уравнения Бесселя.

И так далее. Другими словами, если существует функция Бесселя нулевого порядка, проекция скорости в полярных координатах равна. Найти обтекаемость из уравнения. Таким образом, обтекаемость-это радиусы, расходящиеся от начала координат, а концентрические окружности-это корни уравнения. Дадим цилиндрический контейнер радиуса.

Затем из условия основные уравнения , которое вы определяете Уравнение имеет бесконечное число корней, первый из которых является сущностью. Поэтому она определяется из уравнения. Поэтому период колебаний становится для бесконечно глубоких жидкостей. Для неглубоких жидкостей. Узел вертикального перемещения определяется из уравнения. Так как первый корень уравнения равен