Оглавление:













Коэффициенты трения, тепло- и массопередачи при больших скоростях массообмена. Пленочная теория
- В данном разделе описана простая модель, позволяющая полностью проанализировать зависимость коэффициента трения, теплопередачи и массопереноса от массопереноса. Такие модели приняли одностороннюю модель течения вокруг бесконечно длинной плоской твердой поверхности. С задачей тепломассообмена в одномерном потоке жидкости. Газ был осажден несколькими авторами[6, 11-13]. Например, в рамках теории пленок[11], фазовый переход обоих компонентов бинарной газовой смеси. Высокое требование к скорости массообмена.
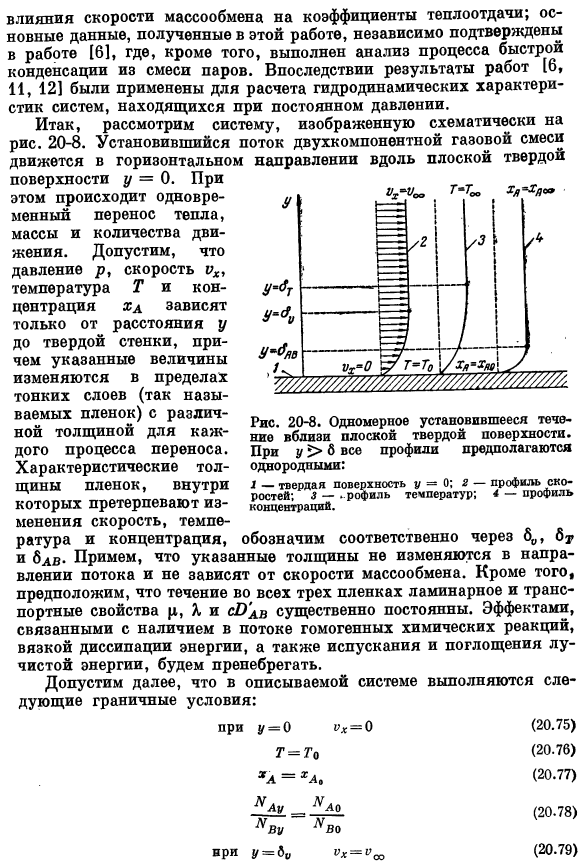
Расчетам была посвящена работа[12] Исследовано влияние скорости массопереноса на коэффициент теплопередачи; основные данные, полученные в данной работе, независимо подтверждены в 61, кроме того, проведен анализ процесса Быстрая конденсация из паровых смесей. Затем мы применили результаты[6, 11, 12]для расчета гидродинамических свойств Фильм) с различной толщиной для каждого процесса передачи. Скорость, температура, и Сосредоточить. А blv-предполагает, что указанная толщина не изменяется и не зависит от расхода Весь поток Свойства Тейлор РД и совместно бы практически постоянной.
Наконец, коротко будет рассмотрен случай, когда конвекция вынужденного потока находится под влиянием объемных сил (смешанная свободная и вынужденная конвекция). Людмила Фирмаль
Наличие однородных химических реакций в потоке, вязкая диссипация энергии и эффекты, связанные с выделением и поглощением Лучистая энергия игнорируется. Кроме того, предположим, что для описываемой системы выполняются следующие граничные условия: 6″, 6Tr:»: zL » 72 ″ g, указывающий направление скорости массы transfer. In добавление, 3 фильма ламинарная подача и транс Приведенные выше условия определяют скорость на краю соответствующей пленки, температуру и граничное значение концентрации, а также отношение молярного расхода вещества Известны сплошные стены.
Задача состоит в том, чтобы получить формулы скоростных, температурных и концентрационных профилей и рассчитать расход по ним Движение к твердой стене, энергия, масса. Также Как выбрать толщину 6, 6 G и BDV так, чтобы результаты теории пленки можно было применить к системе: Представление практического Уравнение сохранения рассматриваемой системы наиболее удобно описывается через поток импульса, энергии и массы относительно фиксированных координат.
Уже в приложении Предполагая, что в ранее выведенных формулах (17.10), (17.31) и (17.32) величины p, vₓ, T и xa зависят только от координаты y、 Уравнение движения Уравнение энергосбережения Непрерывные уравнения Интегрирование этих уравнений и их связь через градиент скорости, температуры и концентрации(17.28), (17.40) и (15.16) в результате формул функций p ^ x, ei и NAy. Получается следующее уравнение: они действительны в области изменения той же координаты y, что и Формула (20.82) — (20.85). Ниже Nao и UVO показывают поток nay и NBy в постоянном состоянии соответственно. Поскольку они однозначно связаны друг с другом, уравнение NBy является Анализ.
Если толщина bn и bg превышает толщину bAv. Тем не менее, мы предполагаем, что поток N Au и NBy постоянны в области y Б » и бу. Единственным обоснованием для таких предположений является отсутствие другой информации о потоке-A (dr и NBᵤ) в рамках модели пленки. Константы справа от уравнения (20.86) — (20.88) представлены значениями импульса, энергии и массового расхода на твердую стенку (ранее неизвестные). Где значение pvy выражается молярным расходом с использованием таблицы. 15.3. Уравнение энтальпии Na и HB представляет собой постоянную теплоемкость веществ A и B、 Отсутствие тепла смешивания. Технические Характеристики XyJy.
Обозначение-поскольку количество положительное, для удобства используется только*.Специфический Система уравнений (20.90)-(20.92) не включает в себя переменные, отличные от px, T, xA и независимой переменной y. интегрирование таких соотношений и использование границ Условие (20.75) — (20.77) дает следующее уравнение для профилей скорости, температуры и концентрации: Используя граничные условия (20.79) — (20.81), находим уравнения для расчета течения»вверх»и»NAq + NB«. Итак, полученное выше уравнение(20.93) — (20.98) прекрасно определяет решение задачи. Эти уравнения имеют частный случай в виде、 Предыдущий раздел: задача диффузии через неподвижную газовую пленку (см.
Раздел 16.2) и задача конденсации газа а в присутствии неподвижного газа в(пример 17-1).Если дано Процедура численного решения задачи о величине потока, физических свойствах среды и толщине пленки, фазовом переходе заключается в следующем: Концентрация, используйте формулу (20.93)-(20.95) AIA профиля скорости и температуры IX предварительно рассчитанные значения расхода Уравнение (20.93)-(20.98) было применимо к системе, но、 Практический интерес, нужно найти толщину x, один из измеряемых параметров. в ka-ISIL удобно выбирать так называемые unsigned 1 / lokalok и kx, lok1.Это предельные коэффициенты кода/ lok、 «Lok и k*, lok в условиях, когда co-i Nvo стремится к нулю.
Коэффициент{замок, » отношение」: Подставляя эти формулы в уравнение (20.96)-(20.98), перепишем последнее в следующий вид: В пределе, для^> 0 и NB₀ — > 0, из Формулы (20.102) — (20.104) получаем нескорректированный коэффициент/ lok, al₀ и K» _ lok отношение к толщине соответствующей пленки. Уравнение (20.105)-(20.107) может быть легко получено путем расширения правой части уравнения (20.102) — (20.104) ряда Тейлора степеней Лгдо и Туво. Преобразуем толщину пленки, определяемую формулой (20.105)-(20.107), в уравнение (20.96)-(20.98). в результате можно увидеть следующее: Эти уравнения представляют собой основные результаты теории кино.
Они устанавливают зависимость сил трения, потока энергии, напряжения сдвига стенок. Молекулярная теплопроводность, и транспортируется к стенке диффузионными потоками от значений NA-NA₀ и NB-NBₒ.As можно видеть из приведенного выше уравнения, в простой системе геометрии потока Конечная скорость массопереноса влияет также на все 3 процесса переноса. Несмотря на то, что формула (20.108)-(20.110) была выведена в случае ламинарной области в предположении, что физические свойства движущейся среды постоянны、 Это качественно верно для систем с различной турбулентностью и физическими свойствами (см. выпуск 20-12).
Для дальнейшего рассмотрения полезно ввести безразмерные переменныеp, R, 0 и связать их определенной зависимостью с коэффициентами потока и обмена. Ниже приведено выражение Вычислите перечисленные величины и с их помощью представьте в безразмерном виде важнейшие уравнения теории кино. Преимущества безразмерных переменныхp, R, 0 и состоит заключаются в следующем Тот. Они значительно облегчают сравнение результатов, полученных различными теориями массопереноса. Безразмерный показатель степени, который образует правую часть уравнения (20.108)-(20.110), прямо пропорционален скорости массопереноса.
Поэтому их обычно называют коэффициентами Скорость и символp: Безразмерная величина, которая появляется в левой части формулы (20.108) — (20.110), называется коэффициентом потока и обозначается символом R. Переменные Rₒ, раб Отношение импульса, энергии и массового расхода к соответствующему потоку, который переносится молекулярным механизмом, передаваемым через межфазную границу объемным потоком. И Используя величиныp и R, уравнение (20.108)-(20.110) можно описать в следующем компактном виде: Примеры использования формулы для расчета скорости тепломассообмена (20.117)-(20.118) приведены в конце настоящего раздела.
- Полученные результаты Сумма а «и К.» Также может быть применена к системам с криволинейными гидродинамическими линиями тока (см. выпуски 20-10 и 20-11). Поправочный коэффициент 0 Влияние скорости массообмена Трансмиссия и массоперенос определяются соотношением. Согласно формулам, приведенным теорией пленки (20.117) и (20.118), поправочные коэффициенты являются: Коэффициент трения, теплота Формулы (20.122)и (20.123) LaccoSwBooT» uwio «^ r f «ei;» рекомендуется использовать при оценке относительного влияния массопереноса на процесс фазового перехода. В соответствии с формулами (20.117) и (20.118) прямой расчет импульса, теплоты и массы потока осуществляется более удобно.
Зависимость, описываемая формулой (20.122) 0(p), показана на рисунке. 20-9.Дополнительные сведения о свойствах величинp, R и 0 см. На рис. 5. 20-12-20-14, выводы Плечевая кость и многие другие теории представлены в удобной для инженерных расчетов форме. Эти результаты показывают, что во время движения вещества А и в приклеиваются к потоку со стенок. Индексыp₀,rg, и fdv положительны, и по мере увеличения скорости массопереноса коэффициент трения, теплопередачи и массопереноса уменьшается. Если масса течет Вещества A и B направляются от потока к стенке, причем величиныp₀, fg и fdv отрицательны, а коэффициенты a ’и k. It увеличивается с увеличением скорости массопереноса.
В этой части будет рассмотрена только гравитационная свободная конвекция на ряде типичных геометрий: вертикальная плоская пластина, горизонтальный кольцевой цилиндр с постоянной температурой поверхности и жидкость, заключенная между двумя стенками плоскостей или двумя концентрическими цилиндрами с различными температурами. Людмила Фирмаль
Корпус вещества А и в Переданный в обратном направлении коэффициент φ соответствует различным процессам переноса, а также поправка, соответствующая конечной скорости массопереноса Знаки могут отличаться друг от друга other. In в связи с этим правила выбора символов потока NAO и NBO очень важны. Более высокая стоимость Nkh считается положительным, если вещество А входит в фазу проблемы, и отрицательным, если оно выходит из этой фазы. Подобные правила знака были введены в поток.
Профили скорости, температуры и концентрации, определяемые уравнением (20.93)-(20.98), могут быть записаны в одном из 2 эквивалентных безразмерных уравнений. Где символ P обозначает безразмерную скорость, температуру и молярную долю, определяемую следующим уравнением: Безразмерная независимая переменная q для каждого из 3 процессов переноса равна: В крайних случаях, когда скорость массопереноса мала, формулы (20.124) и (20.125) принимают линейный вид. Некоторые специфические типы профилей P были найдены в предыдущих главах(например, в разделе 16.2 была решена задача диффузии газа A через неподвижный газ B).
Процесс конденсации вещества а из газовой смеси, содержащей неподвижное вещество в). На рис. 20-10 показаны некоторые из простейших профилей, описанных в Формуле (20.124).Из рисунка следует характер конечного воздействия Массоперенос в виде профилей и коэффициентов межфазного переноса, качественно 1 И то же самое. Приведенный выше график не особенно важен.
Они служат лишь объяснением применения основных уравнений приближенной теории кино Объяснение большинства конвективных процессов тепло-и массообмена Формула, полученная выше, относится к неограниченному flow. In в этом случае локальные значения скорости, температуры и концентрации в потоке могут быть представлены соответствующими терминами. Значения Fco>и Xt на бесконечно большом расстоянии от поверхности обмена. При описании процесса конвективного обмена в замкнутых каналах обычно используется та же зависимость, но、 вместо значений ц, То и XLS они заменяются так называемыми»объемными«значениями: vₓb, TB, XL. указанная замена эквивалентна «отсечению» каждого профиля в точке.
Где соответствующая переменная (скорость, температура или концентрация) достигает своего объемного значения. Операция «резка», как правило, осуществляется в специфической Недооценка поправок из-за больших скоростей массопереноса. Однако существуют и другие способы интерпретации выводов кинематографической теории、 В настоящее время он отсутствует. Основным ограничением теории кино является гипотеза, используемая для существенно одномерных свойств распределения величин p, v2,T и xd.
Общий случай Обосновать обоснованность таких предположений довольно сложно, но, тем не менее, можно ожидать, что результаты теории кино качественно и правильно опишут закономерности этого процесса Транспорт потоков, движущихся по замкнутому каналу с полностью развитым профилем скорости, температуры и concentration. In рамки модели фильма, градиент давления Направление потока не учитывается, уравнение/(20.99); ок не применимо ни к одной из систем, где сопротивление формы играет важную роль, или к системам, где существует градиент давления. Внутри пленки, параллельной сплошной стенке, она занимает значительную часть общего напряжения сдвига пленки.
Толщины гидродинамического, теплового толщины、 Диффузионная пленка является чисто гипотетическим свойством, не зависящим от скорости массопереноса, и может быть проверена путем сравнения выводов теории пленки с экспериментальными данными. Или сделать расчет на основе более реалистичной модели. Предположения о ламинарном характере течения в пленке и неизменности физических свойств среды не являются фундаментальными. Даже если вы откажетесь от вышеприведенных предположений, последствия не будут столь сложными. То есть при анализе системы с движущейся средой с турбулентными и флуктуирующими физическими свойствами(см. задачу 20-12).
Детальный анализ теории пленки в данном разделе обусловлен той значительной исторической ролью, которую эта теория сыграла в развитии методов математического описания массопереноса. Process. In в разделах 20.6 и 20.7 описаны 2 другие более совершенные модели конвективного массопереноса и на их основе рассчитаны более точные значения поправочного коэффициента — Р, р и 0.
Пример применения пленочной модели к системе, содержащей химически активное вещество, уже рассматривался в разделах 16.3 и 16.4.Многие другие практические приложения теории кино Читателей можно найти в монографии[1]. Отсюда В рамках теории пограничного слоя скорость испарения значительно снижается (см. Пример 20-6). Интересно сравнить вычисленное выше значение NAₒ со значением, полученным по формуле (20.2). в последнем случае коэффициенты » i, x, kx, loc- Дай Решение.
Согласно данным, о которых идет речь, молярное отношение потока R В Примере 20-1. ССЕ’а поделился. Сводка скорости массопереноса нню(20.42), для любой массы transfer. As итог Умножение по обе стороны последнего уравнения Если вы установите NB J= 0, вы можете увидеть следующее: Правую часть уравнения (20.138) можно легко вычислить, если известны значения T» Tm и p.
Смотрите также:

