Оглавление:








Коэффициенты трения для течений в трубах
- Используя метод размерного анализа, описанный в разделе 3.7, можно определить факторы, от которых зависит коэффициент трения, определяемый уравнением (6.2). В качестве конкретного примера проанализируем течение жидкости в гладкой горизонтальной трубе длиной а (рис. 6-1, стр. 178). Предположим, что поток стабильный*и что плотность р и вязкость г жидкости являются постоянными. Кроме того, мы предполагаем, что на определенном участке трубы 2 = 0, распределение скорости и давления в центре того же сечения равна P (то есть, точки r = 0, 2 = 0) известны.
Ясно, что характер течения r 0 существенно влияет на распределение скоростей нижней части потока относительно сечения 2 = 0 (если 2> 0).Если участок трубы, соответствующий отрицательному значению координат 2, достаточно длинный, то участок 2 = 0 полностью стабилен, а скорость V равна 2> 0 и не зависит от 2.Если длина участка трубы с отрицательным значением координат 2 очень мала или равна нулю, то при 2> 0 скорость является функцией 2. •В следующем утверждении предполагается, что значения давления и скорости усредняются во времени, а приведенные выше отклонения (см. раздел 5.1) опущены для краткости.
В местах, где пары аммиака смешивались с парами хлористоводородной кислоты, образовывался белый туман из частиц хлористого аммония. Людмила Фирмаль
Сила, действующая со стороны жидкости на внутреннюю стенку трубы как в ламинарном, так и в турбулентном режимах, определяется соотношением Если правые стороны соотношений (6.2) и (6.8) равны друг другу, то получим уравнение коэффициента трения. (6.9) Где обозначает среднюю скорость стационарного движения жидкости в трубе. Следуйте общим правилам, описанным в разделе 3.7, чтобы ввести следующие безразмерные переменные.=π/(в) г * = г / 2); р * =(р-РП)/ р В > быть = о п / п Для этих переменных выражение (6.9) принимает вид: Вы (6.10)) Полученное уравнение справедливо для круглых труб в условиях ламинарного и турбулентного течения.
Таким образом, исходя из уравнения (6.10), для системы, где гидравлическое сопротивление зависит только от вязкой силы и не зависит от формы обтекаемой поверхности, произведение / Be представляет собой безразмерный градиент скорости, усредненный по всей поверхности.
Напомним, что здесь производная (di ’/ dg*) может быть вычислена, как правило, путем решения системы уравнений (3.109)-(3.110) со следующими граничными условиями: если r * = 4_ = 0 «•=( »*=Переменные r * и 0 известных функций ы * = 0 Если бы мы могли решить систему (3.109) — (3.110) с граничными условиями (6.11)-(6.13), то решение имело бы вид: (г«, е*•, не) (6-14)) р * = р *(р*, 0,р*, Кэ) (6.15) Другими словами, решение зависит от всех 3-х безразмерных независимых переменных и еще одного параметра, который появляется в дифференциальном уравнении после приведения к безразмерной форме. Граничное условие (6.11) — (6.13) не вводит в задачу дополнительных безразмерных групп.
Таким образом, производная g* * 1 * *она должна определяться только безразмерными переменными r*, 0, 2 *и Be. Если поставить r * = 0.5 в уравнение этой производной и интегрировать его с переменными r *и 0, то конечное выражение зависит только от числа Рейнольдса и отношения L / P(последнее представляет собой верхнюю границу интеграла по отношению к r*). в результате получается зависимость коэффициента трения от следующих функций: / = /(Ке, Л / Б) (6.16) Таким образом, из размерного анализа, видно, что коэффициент трения зависит только от соотношения числа Рейнольдса и диаметра трубы.
Если выписать набор независимых переменных, достаточных для полного описания рассматриваемых физических явлений, то можно получить тот же результат, не прибегая к основным дифференциальным уравнениям вообще. Согласно L-теореме Бэкингема, функциональная связь между величинами q, элементы которых могут быть представлены в виде комбинации основных элементов, может быть описана как функция q и безразмерных групп (так называемых P-групп). в этом случае ищется функциональная форма соединения 6 величин (pмежду-PB, P, , P, O и B), поэтому из анализа их размерностей К₽>] = «-*:1 ^] =» [П] [Х] = р означает, что у = 3.Из приведенных выше 6 значений можно сформировать 3 отдельные безразмерные группы.
Поскольку выбор ИТЗ па и P-группа является совершенно произвольным, каждый В некоторой степени. теорема l просто говорит, что общее отношение между начальными величинами должно иметь вид: ?(П1, П₂, П«) = 0 или П₈) Однако показанная теорема имеет 1 недостаток. Без предоставления рецептов выбора независимых переменных их относительная значимость не может быть установлена. Поэтому желательно использовать метод, основанный на использовании дифференциальных уравнений движения. Дополнительную информацию о теореме N читатель может найти в литературе[1]. Если профиль скорости сечением 2 = 0 полностью развернут, то производная dm ^ / dm *не зависит от координаты 2*.
В этом случае при интегрировании формулы (6.10) с 2* отображается коэффициент L / O. Это уменьшается на коэффициент P / P перед началом integration. As в результате мы видим, что коэффициент / не зависит от P / P ratio. In другими словами, функциональные зависимости включены. / = /(Быть) (6.17) Если профиль скорости сечения 2 = 0 не полностью расширен, но длина входного сечения мала по сравнению с общей длиной P, то Интеграл над r * умножит интегратор на величину, близкую к P / P. In в этом случае функциональная зависимость коэффициента/также принимает вид формулы (6.17).Соотношение (6.17) справедливо, если а)профиль скорости полностью расширен или б) выполнено условие(P / P) «1».
- Формулы (6.16) и (6.17) весьма полезны для обеспечения возможности систематического представления экспериментальных данных о зависимости перепада давления от объемного течения при ламинарном и турбулентном течении круглых труб. Для очень длинной трубы, например, чтобы сопоставить такие данные, вам нужно использовать кривую 1 (коэффициент трения / безразмерная комбинация зависимого графа P («>p / c. It достаточно создать). Проведено исследование объемной зависимости расхода от потерь давления при различных фиксированных значениях O, p, p. В литературе имеется много экспериментальных данных о зависимости перепада давления от среднего расхода (или объемного расхода) жидкости в трубе.
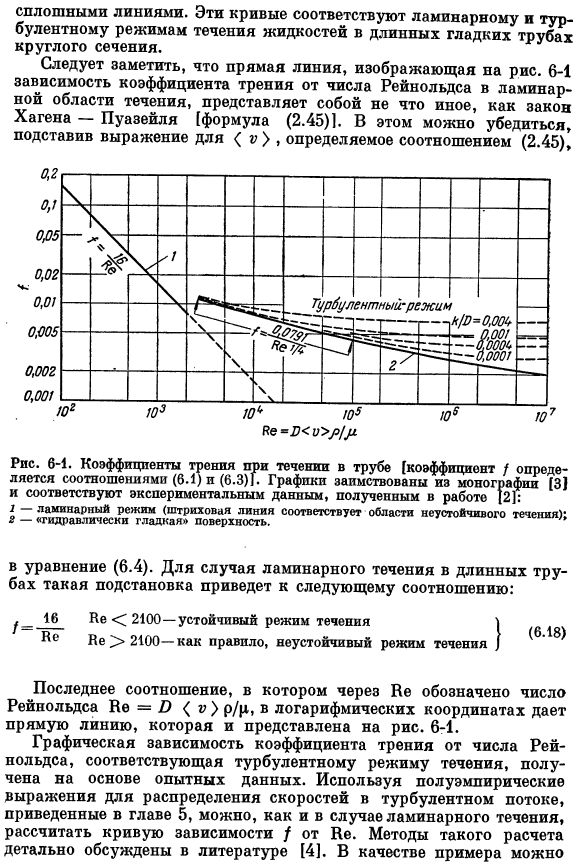
На основе этих данных можно использовать rmula (6.4) для расчета коэффициента трения в зависимости от расхода mnx. Тогда, если мы знаем O, p и p, мы можем создать echl с ИК-зависимостью от числа Рейнольдса коэффициентов/He. Для гладкой трубы кривая показана на рисунке 6-1 Сплошная линия. Эти кривые соответствуют ламинарному и турбулентному состояниям потока жидкости в длинной гладкой трубе круглого сечения. Обратите внимание на прямые линии, нарисованные на рисунке.
Пористая поверхность труб была пропитана хлористоводородной кислотой, а к воздуху были примешаны пары аммиака. Людмила Фирмаль
Зависимость коэффициента трения от числа Рейнольдса в области ламинарного течения потока определяется законом Хагена-пуасселя[уравнение (2.45) 1.Это можно проверить, подставив выражение для, определенного в отношении (2.45). Ре-П / > Ди Рисунок 6-1.Коэффициент трения в потоке в трубе [коэффициент/определяется соотношениями (6.1) и (6.3) 1-график заимствован из экспериментальных данных, полученных в РА 1-ламинарном режиме течения и соответствует (пунктирные линии не видны).、 Преобразуется в выражение (6.4).в случае ламинарного течения в длинной трубе такая подстановка приводит к следующим соотношениям: 16 Ke 2100-устойчивый поток «Ё» не 2100-как правило, неустойчивая жидкостная система.
Последнее соотношение, где Re — число Рейнольдса Ye = B p / p, дает прямую линию в логарифмических координатах. Это показано на рисунке. 6т1. На основе экспериментальных данных получен график зависимости коэффициента трения от числа Рейнольдсов, соответствующих турбулентному режиму. Вы можете рассчитать кривую зависимости/от He, как и в случае ламинарного течения, используя полуописанную формулу распределения скоростей данного турбулентного потока в главе 5.Методы таких расчетов подробно рассмотрены в литературе[4].в качестве примера можно привести Рассмотрим простейшее распределение турбулентной скорости-закон степени* / .: (6.19 )) Где V,=] / mn / p = Y (Po-pb)/ / 2πбб-и α = я-R.
Средний расход по закону (6.19), как легко понять, удовлетворяет следующим соотношениям: (6.20)) Подставляя формулу (6.20) в Формулу (6.4), находим следующий закон сопротивления турбулентности в трубе: / 2 (?^>)(8.56) ’2(0.817)7)(В / Г > Р)’(6-21) •’ке^ 2.1 * 10 «не 10«(6.22) Последняя зависимость, известная как официальная, Блазиус, хорошо описывает экспериментальные данные вплоть до числа Рейнольдса 10. Формула Блазиуса очень полезна для численной оценки. Более строгое соотношение между /и не может быть получено с использованием более точного представления распределения скоростей (например, см.
Задачу 6-6, сформулированную ниже).Для целей инженерных расчетов эти зависимости показаны на схеме. 6-1 (стр. Это связано с тем, что она была оценена путем обработки всех экспериментальных материалов, имеющихся в литературе по турбулентности в трубах. Если внутренняя поверхность трубы шероховата для обеспечения заданной объемной скорости потока через трубу в турбулентном режиме, то требуется резкое падение давления, а не такое, которое соответствует сплошной линии на фиг.1. 6-1.In в этом случае естественно предположить, что коэффициент корреляции трения-число Рейнольдса включает еще 1 параметр — «относительную шероховатость» k / B, tdv k-среднюю высоту шероховатости.
Пунктирная линия 6-1 на рисунке показывает корреляцию f (He), соответствующую различным значениям параметра k / B. наличие шероховатости приводит к тому, что с увеличением числа высоконагруженных поверхностей коэффициент трения/начинает «выходить» на определенное (быть независимым) значение. Конечно, на практике одного параметра k / B недостаточно для описания формы шероховатости и ее распределения по размерам. Для некруглых труб, удобно использовать эмпирический параметр — «средний гидравлический радиус». Где 5-площадь поперечного сечения потока. 2-смоченная часть. В турбулентном режиме уравнение (6.4) и зависимости, показанные на Рис.2, могут быть применены в качестве первого приближения.
Диаметр B должен быть заменен везде. То есть падение давления в некруглой трубе можно приблизительно рассчитать по следующей формуле: (6.24) Значение коэффициента трения, которое должно быть присвоено этой формуле, можно найти в соответствующем графике на рисунке. 6-1.Число Рейнольдса, функцией которого является коэффициент трения/, связано со средней скоростью r >>отношением. (6.25 )) Обратите внимание, что приведенный выше метод расчета не применим в случае ламинарной области(см. задачу 6-8). Пример 6-1.Длина трубы подачи 304,8 скорости к скорости разделения Больше.
Падение давления можно найти при значении He V/. В графе зависимостей he’s he V это значение соответствует определенному числу Рейнольдсов. То, что он знает, может рассчитать средний расход и поток жидкости в трубе. Вы можете использовать дополнительную структуру, если она разрешена следующим графическим решением, как показано на рисунке 6-1: F = f (Be, k / L) — кривая, изображенная на рис.
Прямая линия с наклоном −2 в логарифмических координатах p₀ — = 2.07-105 dyno * cm * ’ = 2.07 * 1СЫg-CM-1.е-1 21 = 20,27 см; B = 30480 см; p = 1 г-см Р = 1.03 СР = 0.0103 г-см-1.0-1 20.27-1 1 /(2.07•10 «)•20.27 0,0103 г 2-30 480-1 А он нет-1.63-10 *Прямая линия, описываемая формулой (6.28), проходит через точки (/=1.0, He = 1.63-10*) и (/=0.01, Be = 1.63-105).Продолжая эту прямую линию до пересечения с кривой, соответствующей значению параметра x / 0 = 0.00023 (6.27), получим решение системы уравнений (6.27)-(6.28). (6.30) Отсюда и> = — y21r.
Смотрите также:

