Оглавление:







Коэффициенты трения для насадочных колонн
- В предыдущем разделе мы описали корреляцию коэффициентов трения в 2 очень простых гидродинамических системах, но они до сих пор часто появляются в инженерных расчетах, поскольку играют важную роль во многих процессах химической технологии. В литературе существует корреляция других систем: поток вблизи вращающегося диска, поток вокруг цилиндра, поток вокруг пучка цилиндрических трубок, поток каналов с перегородками. Важные системы для химической промышленности можно найти в руководстве инженера-химика [14]. В монографии Шлихтинга [4] рассмотрен ряд систем, в которых проводились фундаментальные исследования по гидродинамике и аэродинамике.
Особый интерес с точки зрения химической технологии представляет заправочная колонна, являющаяся одним из наиболее распространенных типов массообменных устройств. Существует 2 теоретических подхода к оценке падения давления в насадочном слое. В соответствии с одним из этих подходов заполненные колонны рассматриваются как ответвленные системы изогнутых труб переменного сечения. К этой системе применяются результаты теории, разработанной для одной прямой трубы.
Для точек, находящихся на больших расстояниях от критической точки, точное решение дифференциальных уравнений, описывающих поток и перенос тепла в пограничном слое, требует сложных вычислений. Людмила Фирмаль
Другой подход заключается в том, что упакованный слой рассматривается как совокупность большого количества твердых частиц, обтекаемых внешним потоком, и падение давления в слое рассчитывается путем суммирования гидродинамического сопротивления, оказываемого каждой частицей в отдельности. [15, 16].Этому уделяется основное внимание, поскольку подход, основанный на Трубной модели, является более эффективным, что подтверждается практикой.
В качестве материала сопла можно использовать различные сопловые изделия для контактных устройств, изготавливаемых в шаровой, цилиндрической и других отраслях промышленности[3,17].Далее, предполагается, что сопла равномерно распределены повсюду, и так называемое «образование каналов» в системе не происходит(в реальных условиях явление образования каналов очень распространено, и следующая формула не может быть применена к этим условиям).кроме того, предполагается, что характерный размер частиц сопла мал по сравнению с диаметром колонны, в которую заключено сопло, а диаметр колонны постоянен. Коэффициент трения слоя наполнителя определяется по аналогии с формулой (6.4).
Здесь показано: D: through-средний размер частиц сопла. throughv₀-так называемая «скорость торможения» (то есть средняя линейная скорость жидкости, движущейся вдоль колонны при отсутствии сопла).Через L длина упакованного layer. It рекомендуется самостоятельно оценивать значение коэффициента трения в условиях ламинарного и турбулентного течения. В ламинарном потоке круглой трубы с радиусом R средний расход, как показано в разделе 2.3, получается по следующему уравнению: (РА-Р) Д2 ′) 8pL Здесь мы предполагаем, что уплотнительный слой представляет собой трубу с очень сложной формой поперечного сечения, и Rₐ обозначает гидравлический радиус этой воображаемой трубы как 1 см.
Уравнение (6.23)]. Тогда формула для средней скорости течения свободной (то есть не занятой твердыми частицами) части поперечного сечения слоя выглядит следующим образом: (6.60) (Д) (р «-р) д * (6.61) 2р£ Гидравлический радиус может быть представлен «объемной долей пустоты» е и площадью а смачиваемой поверхности на единицу объема слоя. Площадь свободной части сечения смачиваемого слоя / Свободное пространство -)- Объем пустот (6.62) Величина а связана с отношением «удельной площади поверхности» (А₀, относительно общей поверхности всех частиц в сопле, к объему, занимаемому этими частицами): «=»(1-8) (6.63)) Удельная площадь поверхности определяет средний размер частиц ОА.
Если частица сопла сферическая, то легко увидеть, что значение Dₐ, определенное уравнением (6.64), соответствует истинному размеру частицы. Заметим, что средняя скорость пространства между частицами не представляет практического интереса. Для инженеров-химиков важно знать величину убывающей скорости r₀, а не эту величину. Последнее связано со средней скоростью в соотношении v среднее. Теперь замените выражение(6.62)-(6.64) Poizieri Хаген (6.61).В результате (П » — РБ)» » 2flL » l (1-8)2 Изменить, получить (П-ПБ) Я£.
- Описание упаковки для ламинарного потока p для слоя с моделью трубы с гидравлическим радиусом расход часто слишком высок для определенного градиента давления. Поэтому ожидается, что правая часть уравнения (6.66) будет меньше, если использовать более совершенную гидродинамическую модель заполняющего слоя. Кроме того, при выводе уравнения (6.66) предполагалось, что каждый элемент жидкости будет неявно проходить через путь в слое длины, совпадающей с длиной столба L.
Конечно, на практике жидкий элемент описывает очень сложные элементы в движении по траектории, и общая длина их путей может значительно превышать длину столба L (до 1,5 раза).в результате истинное значение V₀ должно быть меньше пятна, определенного в правой части уравнения (6.66). Результаты измерений показывают, что для проведения эксперимента и корректировки теоретической формулы (6.66) необходимо заменить коэффициент 2 в знаменателе справа от этой формулы на коэффициент со значением 4-5. При большом количестве имеющихся экспериментальных данных можно сделать вывод, что этот коэффициент должен быть равен ss / to.
Ламинарный пограничный слой покрывает часть поверхности вверх по потоку, который отрывается от поверхности шара, создавая хаотическое течение потока вдоль его нижней части. Людмила Фирмаль
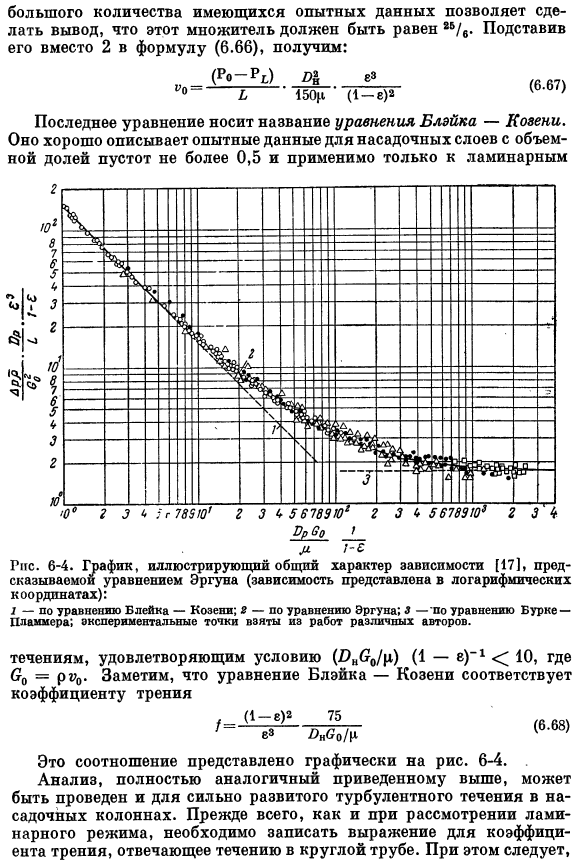
Подставляя его вместо 2 в выражение (6.66), получим: (р «-р) ОС е» Л ’150р’ (1-с) S (6.67) Последнее уравнение называется уравнением Блейка-Козени. Это хорошо объясняет экспериментальные данные насыпного слоя с объемной долей пустоты менее 0,5 и может быть применено только к ламинарному течению Выполняется условие потока (DKGJp) (1-c) −110, Где Gₒ=pr₀. Отметим, что формула Блейка-Козени соответствует коэффициенту трения (1-й) 2 75 Гонн» Идти / Ч. (6.68) Это соотношение графически показано на рисунке. 6-4. 。 Анализ, который полностью аналогичен приведенному выше, также может быть выполнен для высокоразвитой турбулентности в насадочной колонне.
Прежде всего, необходимо записать формулу для коэффициента трения, который соответствует течению в круглой трубе, как при рассмотрении ламинарного режима. Следовать Но учтите, что в случае сильно развитой турбулентной течи в трубах, где есть заметная шероховатость на стенках, коэффициент трения зависит только от степени шероховатости. Предполагая, что все заполненные слои имеют приблизительно одинаковые характеристики шероховатости, для турбулентного течения в таком слое можно ввести универсальное значение коэффициента трения.
Это значение черепа указывает на/₀.Выполните линию вывода, описанную в разделе 6.2, и выполните следующие замены в соответствующем выражении: v₀ / e; 4RA; Rₐ= e / a; a = a»(i-e); Dₐ= 6 / ao. Тогда мы найдем: Л₽2Д д° » Е3 Из экспериментальных данных видно, что она равна 6 /₀= 3.5.Подставляя это значение в соотношение (6.69), получим: Последнее уравнение называется уравнением Берка-Пламмера. Допустимо для потоков, удовлетворяющих условиям (DeGo / H) (1 — » Г1> Ю3— Коэффициент трения, соответствующий этому уравнению (6.71) Заметим, что в турбулентной области течения зависимость/от β отличается от соответствующей зависимости ламинарной области.
Если уравнение Блейка-Козени, эффективное для ламинарного течения, должным образом объединить с уравнением Берка-Пламмера, описывающим турбулентное течение, то получается следующее соотношение: Po-Pₜ150 / U > ₀ (1-e)3, l, 75pvj 1-8 L DIin3Oya8 В безразмерном формате формат равен[18]. (6.72) (6.73)) Это называется уравнением Элгана. Используя соотношение (6.73), мы смогли полностью объяснить экспериментальные данные для gas. In в этом случае плотность газа при давлении, равном среднему арифметическому давления на входе и выходе из колонны, использовалась в качестве плотности р.
Однако при резком падении давления представляется более целесообразным применить соотношение (6.72) и записать градиенты давления, содержащиеся в нем в производной форме. Заметим, что величина Gₒ постоянна во всем слое, в то время как величина r> the изменяется вдоль толщины слоя в случае сжимаемых газов. Величины DH, попадающие в соотношения (6.72) и (6.73), определяются по формуле (6.64). При высоких скоростях потока первый член в правой части уравнения (6.73) становится незначительным по сравнению со вторым членом, который является уравнением Бурка Пламмера. Для медленного, 2-й член может быть проигнорирован и наоборот.
Из уравнения (6.75) получаем уравнение Блейка-козени. На рис. 6-4 показаны общие характеристики зависимостей, описанных в уравнениях (6.67), (6.70) и (6.73). следует подчеркнуть, что уравнение Элгана является лишь 1 из многих уравнений, предложенных для расчета потерь давления в насадочной колонне*. Вопрос для обсуждения Есть. Трения в потоке кольца — РОА zaille. 10. * Проблемы, связанные с гидродинамикой жены в литературе[19]. — Пршич. Эд. 14.Мы поговорим.
Смотрите также:
| Коэффициенты трения для течений в трубах | Межфазный перенос в изотермических системах. Задачи |
| Коэффициенты трения для потоков, обтекающих сферические частицы | Макроскопический баланс массы |

