Оглавление:










Коэффициенты теплоотдачи при вынужденной конвекции в трубах
- Коэффициент теплопередачи при вынужденной конвекции в трубе. Вопросы, связанные с математическим описанием процесса нагрева и охлаждения жидкостей и газов. Трубы очень важны для практического использования. Многие научные работы и монографии посвящены этим вопросам и содержат множество приближенных формул. Рассчитайте теплопередачу в трубе. Цель этого раздела-помочь читателям понять наиболее надежные и частые корреляции, встречающиеся в литературе. Во-первых, мы показываем обобщение метода размерного анализа, описанного в разделе 10.6, и используем этот метод для установления формы корреляции коэффициентов теплопередачи. Система принудительной конвекции.
В частности, рассмотрим установившийся поток жидкости в кольцевой трубе, показанной на рисунке 1. 13-1.Распределение скорости Известно также, что поперечное сечение Z имеет постоянную температуру выхода на поверхность нагреваемого участка трубы, которая лежит между плоскостями z = 0 и z = L. физические свойства жидкостей p, p, Cp и Сначала также предполагается, что L является постоянной величиной. Однако в дальнейшем рассмотрено влияние температурной зависимости вязкости Р. При надлежащих условиях эти Эффект очень важен.
Кинетическая теория объясняет напряжения трения в текущем газе тем, что молекулы движутся вперед и назад между слоями газа, текущими с различными скоростями. Людмила Фирмаль
Для труб с радиусом R и длиной L, общее количество тепла, поступающего в жидкость от стенки трубы в единицу времени、 Формула = J⁺ ⁺ ⁺ определена в dlde DL (13.19).Эта формула применима как к ламинарным, так и к турбулентным течениям. Знак плюс здесь ответит физическое состояние, при котором тепло, распространяющееся в отрицательном направлении оси z, входит в system. To право на выражение. Чтобы решить полученное уравнение относительно (13.2) и (13.19) a, получим уравнения, умножим стороны (13.20) на P / X и введем следующую безразмерную Переменные: g * = r / P; z= z / D; T * = = (T*T»)/(Tbₗ-To); Nuₜ= » x2E /X.
Далее находим следующее: следовательно, безразмерный коэффициент теплопередачи Nuₓ( Nusselt) — фактически безразмерный градиент температуры, усредненный на плоскости теплообмена. Безразмерный градиент температуры, как правило、 Определить путем дифференцирования уравнение T *, полученное в результате решения системы уравнений (10.113)-(10.115) со следующими граничными условиями: Переменные r *и 0 равны R * =(>13.22) о* = 0 равны r»=у (13.23) p = 0 равны 2 * = 0, r * = 0 (13.24)Г * = 1 для i * = 0 (13.25)T * = 0 для>•=-! (13.26) в случае турбулентности, все В следующем тексте вы должны предположить, что значения температуры, давления и скорости усредняются во времени.
Для краткости эти значения записаны выше без тире. Границы Условия (13.22)-(13.26) не включают никаких дополнительных безразмерных групп, кроме тех, которые содержатся в дифференциальном уравнении (10.113)-(10.115).Из этого можно сделать вывод Усредненное по времени распределение безразмерной температуры T должно быть выражено зависимостью T * =Г(r, 0,**; Re, Pr, Br) (13.27). С зависимостями (13.27) и зависимостями (6.14) и (6.15) легко увидеть, что для неизотермических систем корреляция является гораздо более сложной формой, чем для этого случая. Изотермическая система.
Подставляя зависимости (13.21) в правую часть соотношения (13.27), получаем: Nu₁ = Nu₁ (Re, Pr, Br, L / D) (13.28) В реально встречающейся системе эффект вязкой диссипации не играет существенной роли, поэтому число Бринкмана не может быть включено в определенное число Параметр задачи. Аналогично, зависимость (13.28) может быть представлена в более простой форме. Nu₁=Nu₁ (Re, Pr, L / D) следовательно, из размерного анализа、 Вынужденная конвекция, коэффициент теплопередачи а в трубе при постоянной температуре на стенке могут быть соотнесены в виде зависимости числа Рейнольдса от безразмерной группы Nuj.
Аналогичные корреляции могут быть получены для коэффициентов aa, a | n и alok от Прандтля, а также от геометрического фактора L / D(см. задачу 13-7).Nuₐ=Nuₐ(Ре, Ор, Л / Д) НУИНУ = ну / ₙ(Ре, Ор, Л / Д)NunoK = NunoK(Ре, Ор, Л / Д), где Nuₐ= Оер / х, Ну ₙ= от ^ .D / X, Nu » Ok = unlock — ^ A-общая форма корреляции(13.29)-(13.32) также может быть выявлена на основе теоремы l. Букингем был ранее сформулирован и обсужден при рассмотрении отношений (6.16).Очевидно, что в самом общем виде коэффициент теплопередачи a равен Из физических свойств среды (то есть из p, p, Cp и X), геометрических свойств D и L и средней скорости потока.
Основные элементы любой задачи Теплопередача равна массе m, длине I, времени t, температуре T. согласно теореме Букингема L, в этом случае нам нужно 4 взаимосвязанных (13.29) (13.30) (13.31). (13.32) безразмерная группа. Действительно, с помощью этой теоремы невозможно установить определенный способ выбора независимых variables. So далеко, через интервал Характеристики рассматриваемой системы температурные, физические характеристики среды остаются постоянными. Если существует большая разница температур в системе, это предположение является Это приводит к серьезным последствиям errors. At при этом наиболее существенные изменения получают значения C и p.
Обобщенная корреляция с учетом температурной зависимости Вязкость может быть получена на основе следующих простых соображений: если разность температур в системе не слишком велика, то вязкость pi ряда Тейлора расширяется. Температура стенки трубы T = Ta:(13.33 a), где Tso-значение вязкости при температуре, равной температуре стенки. Заменяет частичный дифференциал (dr / dT), содержащийся в разложении (13.33 а) приближенное разностное уравнение (п-\»о»)/ (^б-го), Р » ⁸t-средняя температура объема потока, и организации, является вязкость при температуре t б.
В Вместо соотношения (13.33 a) найдите результат: преобразуйте выражение(13.336) так, чтобы его левая сторона имела вид безразмерной вязкости P*. (13.33 b)от соединения (13.33 c) Таким образом, вязкость Р, описываемая разложением(13.33 а), заменяется исходной системой дифференциальных уравнений конвективного теплообмена и этой размерностью.
Распределение результатов системы безразмерной температуры[аналог распределения(13.27) 1 включен в качестве дополнительного 1(по сравнению с случаем| l = const) Значение аргумента, значение U / p₀.Таким образом, вычисленная выше корреляция каждого числа нуссельта выражается следующим образом: Nu = Nu(Re, Pr, L / D, pb / po) (13.33 g> Корреляция в виде соотношения (13,33 г) является первой[61.Если плотность среды Р существенно изменяется с температурой, то система Естественная конвекция. Эффект не может быть рассмотрен простым добавлением числа Гласса к безразмерной группе, которая появляется в предыдущих корреляциях.
Детальный анализ [71.При ламинарном режиме происходит конвективный теплообмен в трубе, где одновременно присутствуют температурные зависимости величины р и величины Р. Дебаты очень острые Однако сложный показатель теплопередачи, который наблюдается в этом случае, не входит в задачи данной книги. Результаты, которые были получены ранее, основаны на размерном анализе Большое практическое значение, что значительно облегчает обработку экспериментальных данных по теплу transfer.
Отношение (13,33 г), значение а равно 8 Физической переменной (о; ; п; р; п; р; с, р; х; л), эта зависимость может быть уменьшена в зависимости от количества безразмерных нуссельта, только 4 безразмерных групп. (Ре; Л / Д; пр; НК / пн).Такое уменьшение числа независимых переменных может значительно сократить число экспериментов, необходимых для установления явной формы корреляции. Например、 Для изучения влияния всех возможных комбинаций из 8 независимых переменных необходимо провести 10 экспериментов, так как каждый из них проходит через 10 дискретных значений. Случай 4 независимые переменные таких экспериментов требуют только 10*.Корреляция, полученная из размерного анализа.
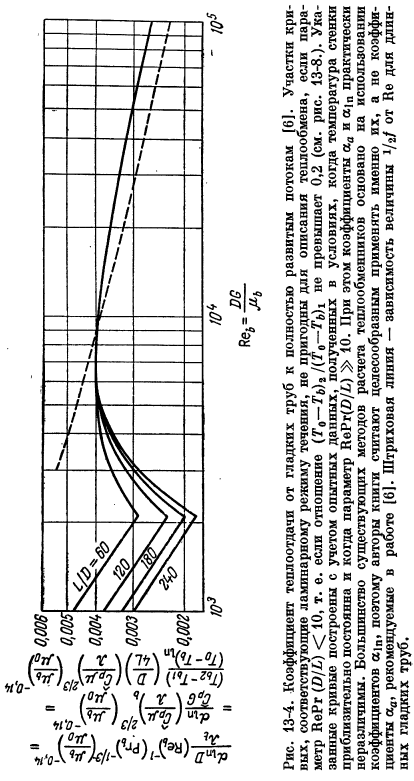
Теперь давайте подумаем о некоторых известных корреляциях. Опишите теплообмен в трубе. На рис. 13-4 показана корреляция между Сидером и Тейтом [6].она связана с развитым потоком в почти постоянной гладкой трубе. Температура их стенок. Эта корреляция совпадает с соотношением (13.33 г), которое дает очень четкое представление об общей закономерности теплообмена при протекании в трубе. Когда подавать заявку Среди указанных корреляций, характеризующих физическую характеристику, следует отметить, что все величины, содержащиеся в ней, за исключением вязкости p₀, соответствуют температуре (Gm +Tᵢ₂)/ 2 Температура (U01 +Т₀₂)/ 2.Число Рейнольдса определяется здесь как Re₆= DG / pb = Du> / Spb.
Такое определение удобно в том смысле, что. Экспериментально установлено[8], что переход от ламинарного течения к турбулентному, в данном случае величина p, даже обычно Re;,= начинается примерно в 2100 году. Необыкновенно. Радиальные изменения. Величина G = w / S-(p r>называется массовым расходом. Для сильно развитой турбулентности кривая, соответствующая (L / D)>> 10, объединить в 1 строку. При условии Reb> 20 000 Эта линия удовлетворяет уравнению ((13.34).Это описывает экспериментальные результаты с точностью±20%.
Диапазон чисел Рейнольдса Re, число Прандтля в диапазоне 0.6〜10 *〜10⁵ и значение коэффициента (L / D)> 10.In случай ламинарного течения, коэффициент корреляции Форма теплопередачи выглядит следующим образом: использование этой корреляции является теоретическим уравнением ГРЕТСА эмпирического обобщения[61] [9]、 Теплопередача от стенки трубы при постоянной температуре к полностью развитому ламинарному потоку[опорное уравнение (13.41)1.Формула (13.35) очень хороша( Точность±20%) приведены экспериментальные данные для системы, удовлетворяющей условию RePr (D / L)> 10.At ниже объемные потоки, истинное значение a, n значительно занижено. Теплообмен в переходной гидродинамической области, т. е.
Поэтому при проектировании тепловой установки в переходном гидродинамическом режиме Старайтесь избегать его как можно больше.13-4, соответствующая переходной области графика течения кривой на рисунке, была подтверждена во многих экспериментах, но результаты не таковы Надежен, как и в случае полностью развитых ламинарных и турбулентных режимов. Общая характеристика кривой, показанной на рис.
- Исследование. Во-первых, если жидкость или газ с заданными физическими свойствами протекает через нагретую часть трубы (значения L и D известны). Вертикальная координата кривой пропорциональна безразмерной разнице температур(Tg-Tg)/(Tt-T») в движущемся потоке. В этих условиях по мере увеличения объемного расхода、 При числе Рейнольдса температура потока на выходе из трубы сначала снижается (до достижения критического значения 2100 Re₆), а затем повышается(максимум Момент, когда число Рейнольдса достигло примерно 8000), и, наконец, начинает уменьшаться again. It также важно отметить, что коэффициент теплопередачи О / П в значительной степени зависит.
Только в случае ламинарной области, отношение L / Z).Число Рейнольдсов превышает 8000, значение L / D показано на рисунке 13-4, влияние коэффициента L / D существенно Он полностью исчезает. График показан на рисунке. Существует некоторое сходство с диаграммой коэффициента трения, приведенной на рис. 13-4. 6-1 в физическом смысле. Значения, построенные вдоль оси абсцисс этих графиков, различаются widely. In область высокоразвитой турбулентности (Re«> 10 000), ордината пропорциональна коэффициенту Теплопередача изменяется с изменением числа Рейнольдса, и величина гладкой трубы/ / 2 почти одинакова.
Это означает, например, что определенное количество тепла передается через неподвижный слой газа при данных температурных условиях независимо от давления газа. Людмила Фирмаль
Это Колборн. Эмпирическая аналогия течения в гладкой длинной трубе при re₆> 10 000:(13.36), где величина/ n подробно описывается соотношением раствора ГРЕТСА и Ребека9. Она описана в монографии (2).Кроме того, величина/ / 2 может быть получена из графика, показанного сплошной линией (турбулентная область) на рисунке 6-1. Вам нужно определить число Рейнольдса как DG / fy, используя корреляцию (13.36).Индекс / здесь и отношение (13.37), соответствующее значение Снимайте при так называемой «температуре пленки» равной (Tb + Ta)/ 2.Где Tb и Tu-средние значения объемной и пристенной температур, определенные из соответствующих значений. Первое и последнее значение температуры трубы.
Значение СР в знаменателе в правой части формулы(13.37) соответствует температуре го. Физическая природа потока Постоянная по длине трубы, график 13-4, показанный на рисунке, показывает зависимость/ n от Рейнольдса number. It совершенно ясно, что аналогия (13.36) не применима. Ре 10,000.Эта аналогия будет совершенно неэффективна в случае турбулентности, когда стенки полностью развиты в грубой трубе. Шероховатость гораздо более выражена, чем значение коэффициента трения / U. В заключение необходимо сделать еще одно замечание по поводу использования еще 1. Для характеристики тока в канале корреляции 13-4, некруглого сечения, приведенного на рис. figure.
Может применяться для высокоразвитых турбулентных течений. [3] Понятие среднего гидравлического радиуса, которое определяется формулой (6.23). для описания теплообмена в некруглой трубе используют эмпирическую корреляцию Для круглых труб число Рейнольдса и число нуссельта, входящие в указанную корреляцию, должны заменить диаметр D со средним гидравлическим радиусом в 4 раза больше 4R. Simple. 13-4, корреляция, показанная на рисунке, показала, что она очень подходит для решения многих инженерных задач. Однако отображение ламинарного и турбулентного режимов в кадре Одна сетка координатных линий слишком упрощена.
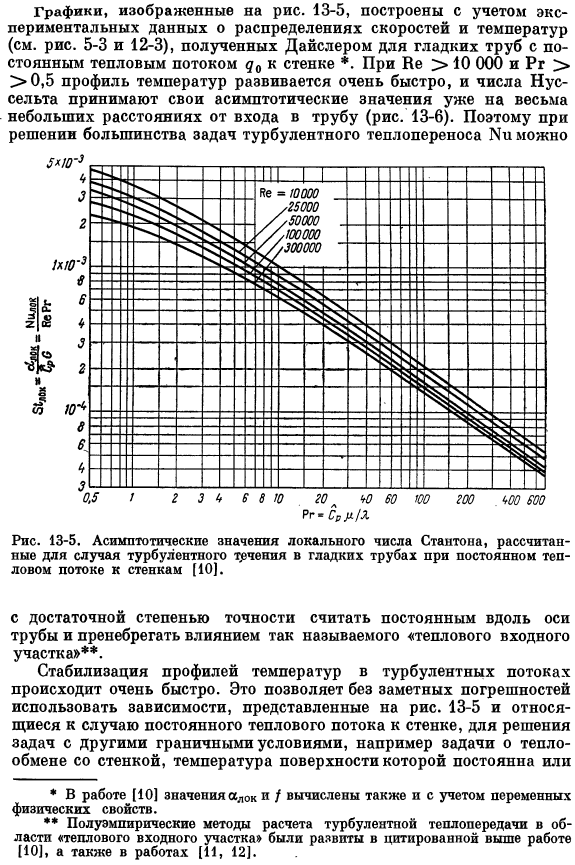
Ниже приводится более точная корреляция, которая действительна только в одном из вышеупомянутых режимов Корреляция получена на основе экспериментальных данных по распределению температуры. Опишите теплообмен в условиях постоянной высокоразвитой турбулентности (Re> 10 000) Физические характеристики потока и число Прандтля более 0,5 используют хорошо известную корреляцию разрушителя[10].Эта корреляция графически показана на рисунке. 13-5, здесь. Вертикальная ось представляет собой так называемое число Стэнтона St, которое определяется как St = d / C / G = Nu /(RePr). •Первое последующее наблюдение (до примера 13-2) Чтение-можно пропустить.
Для читателей, заинтересованных в более подробных корреляциях, имеет смысл продолжить чтение, но я бы предложил вам сразу перейти к примеру 13-2. График показан на рисунке. 13-5 строится с учетом экспериментальных данных по распределению скорости и температуры (см. Рисунки 5-3 и 12-3). Тепловой поток d₀ в стенку представляет собой постоянную трубу*. При Re> 10 000 и Pr > > 0,5 температурный профиль развивается очень быстро, и число Нусельта становится асимптотическим.
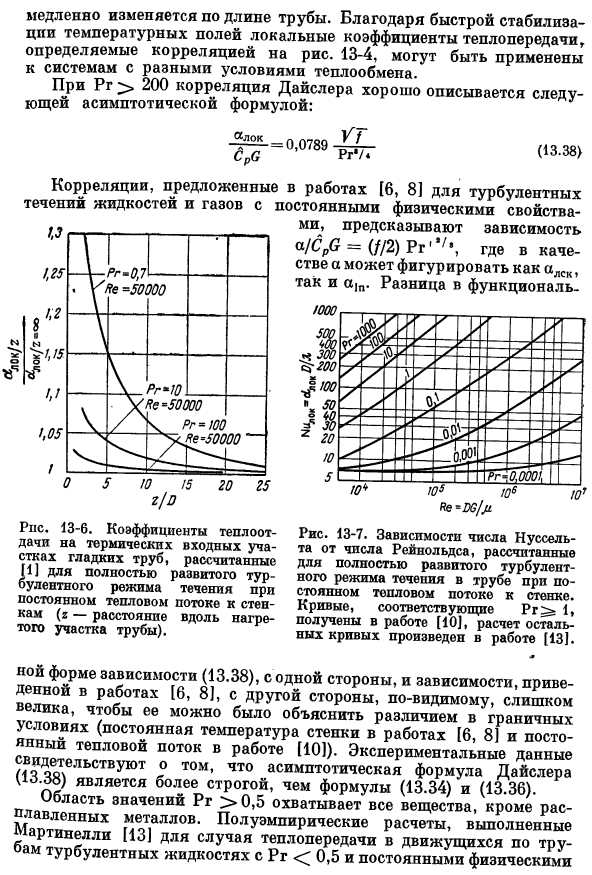
Значение, если расстояние от входа в трубу очень короткий (рис. 13-6).Поэтому, если решить большинство задач турбулентного теплообмена, то Ну будет достаточно большим. Точность считается постоянной вдоль оси трубы и должна игнорировать влияние так называемого «участка подвода тепла»**.Стабилизация температурного профиля турбулентности Это будет очень быстро. Это позволяет использовать зависимости, показанные на рисунке 1, без каких-либо заметных ошибок.
Связанные со случаем постоянного теплового потока Для решения задач со стенами, другими граничными условиями, учитывают, например, задачу теплообмена со стенами, где температура поверхности постоянна, или переменные величины [10] значения alok и f были также рассчитаны для физических характеристик. * * Полуэмпирическим методом расчета турбулентного теплообмена в области «сечения подвода тепла» является、 Он цитируется в[10]и[11, 12]выше. Медленно изменяйте длину трубы. Локальный коэффициент, обусловленный быстрой стабилизацией температурного поля Теплопередача 13-4, которая определяется соотношением диаграмм, может быть применена к системам с различными условиями теплопередачи.
Для PR> 200, то Deisler корреляция хорошо объяснил Следующие асимптотические выражения:-^-= 0,0789-^-(13.38> [6、8]предложена корреляция для турбулентного течения жидкостей и газов с определенными физическими величинами С одной стороны, зависимость, заданная в форме свойства зависимости (13.38), а с другой стороны[6, 81], очевидно, слишком велика и невозможна Различие граничных условий объясняется постоянной температурой стенки[6, 8] и постоянным тепловым потоком 1101.Экспериментальные данные показывают Асимптотическая формула дейслера (13.38) строже, чем формулы (13.34) и (13.36). Диапазон значений Pr> 0,5 охватывает все вещества, кроме расплавов Металл.
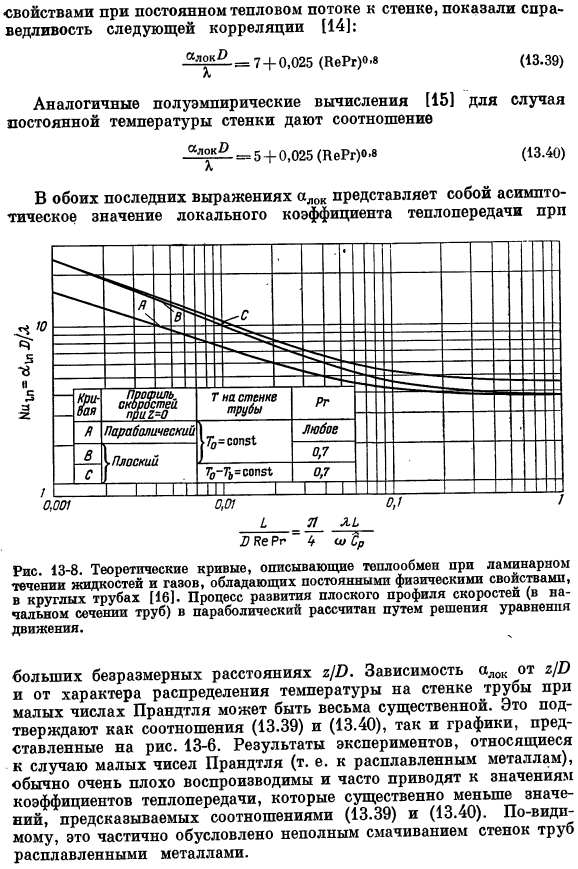
Полуэмпирические расчеты, выполненные Мартинелли[13], основаны на Pr 0,5 и в случае теплопередачи турбулентных жидкостей, движущихся в трубе с определенными физическими свойствами. Характеристики при постоянном тепловом потоке к стенке показали следующую корреляцию [14]: ■ З?! «⁰ ⁰ ⁰ ⁰ ⁰ ⁰ ⁰ ⁰ ⁰ ⁰=7 + 0,025 (repr)» ’«(13.39) аналогично Полуэмпирический расчет[15], когда температура стенки постоянна, дает соотношение-l°kO = 5 + 0.025 (RePr) 0> 8 (13.40). Alok представляет собой асимптотическое значение локального коэффициента теплопередачи prp. 13-8.Теоретическая кривая теплопередачи в ламинарном потоке Жидкости и газы с определенными физическими свойствами в кольцевой трубе[16].
Процесс превращения плоского профиля скорости (в первом сечении трубы) в параболу Он рассчитывается путем решения уравнения движения. Зависимость Модер на характер распределения температуры большого безразмерного расстояния Z / Д з / д, а также небольшое количество стенки трубы Прантл очень важен. Это подтверждается как соотношением (13.39) и (13.40), так и диаграммой, приведенной на рисунке. 13-6.Экспериментальные результаты связанные Когда число Прандтля мало(то есть расплавленный металл), воспроизводимость обычно очень низкая, что часто приводит к значению коэффициента теплопередачи.
Меньше значения, предсказанного соотношением (13.39) и (13.40).По-видимому, это отчасти связано с неполным увлажнением стенок трубы расплавленным металлом. Соотношение Дислер [101] и Мартинелли [13] графически нарисованы непараллельными линиями, как показано на рисунке 1. 13-5.、 Показан точный поток числа нуссельта и функция C числа строк. только наблюдается в оче) Pr. In буква теоретической работы Ламинарный поток жидкостей и газов, проходящий через трубу с определенными физическими свойствами. Значения найденных Nu, Nu показаны на рисунке.13-8 для различных граничных условий.
Отметим, что в области ламинарного течения количество Nu в значительной степени зависит от соотношения L / D и характера распределения температуры стенок трубы. Турбулентный режим, при котором подобная зависимость выражена очень слабо (см. рис. 13-4).Все кривые показаны на рисунке. 13-8, с соответствующей асимптотой (L / D) — ►co. In случай «постоянной Т» на полностью развитой стенке курса, асимптотическое значение NU |ₙ= 3,6 разность To-Tb Асимптотика eNuₗₙ = ⁴в / Х₁ = 4.364.
Кривая а, созданная расчетом Гретца[9], показывает первую 1.О теплопередаче в условиях Вынужденная конвекция, полученная на основе системы уравнений сохранения.
Если длина L мала или объемный поток велик, то решение Гретца является Левек [91: Nujₙ= l, 62 (RePrD / L)’), = l, 75 (wCp / XZ.) Л) (13.41) значение (wCₚl\ л)=простые асимптотические выражения первой оценке (l / 4) RePr (D / L), содержащийся в этой формуле, иногда называется числом GRETS и обозначается Gr*.Соотношения (13.41) формируют основу полуэмпирической зависимости (13.35).Однако следует отметить, что эмпирический коэффициент 1.38, который включен в Формулу (13.35), отличается от коэффициента 1.62 точного решения, соответствующего ламинарному течению Обсуждается влияние большой разницы температур, наблюдаемой в экспериментальных условиях. Пример 13-2 расчет трубчатых нагревателей.
Если давление воздуха составляет 1 бар, то его необходимо нагреть до температуры HO. To для этого предусматривается прокачка воздуха с массовой скоростью 31,75 кг-ч’1 через длинную прямую трубку с внутренней скоростью. Нагрев с диаметром 5,1 см n*в некоторых исследованиях вместо соотношения (1141) появляется погрешность точного коэффициента 1,75 с использованием коэффициента 2,0.Луг. Почему?
Смотрите также:

