Оглавление:






Коэффициенты массоотдачи для потока в трубах
- Большая часть данных о массопереносе между жидкостью и стенкой трубы была получена с использованием увлажненной колонки. Это устройство состоит из вертикальной части трубы круглого сечения, по которой обычно поднимается газ. Летучая жидкость течет по внутренней поверхности трубы, испаряется и превращается в газовый поток. Основная причина, по которой колонны с влажными стенками используются при изучении массопереноса, — это определенность границы раздела. Это позволяет определить истинный коэффициент массопереноса, например , а не произведение.
Последний на границе раздела фаз является в основном чистым, поскольку газ обычно слабо растворяется в жидкости. Жидкость может подаваться при температуре адиабатического насыщения*.Если колонна работает в адиабатических условиях, то концентрация диффундирующих компонентов в газовой фазе на границе раздела фаз постоянна, так как жидкость сохраняет температуру при прохождении через колонну. Колонны с влажными стенками могут использоваться как в случае ламинарного течения, так и в случае газофазной турбулентности, но необходимо соблюдать осторожность, чтобы избежать образования волн на границе раздела газ-жидкость. Это связано с тем, что волны затрудняют определение интерфейса.
Он безразмерный и подобен числу Нуссельта, с которым мы встретимся при изучении конвективного теплообмена. Людмила Фирмаль
По-видимому, наиболее правильное значение скорости должно быть введено в число Рейнольдса для объяснения движения Газ-это сумма скоростей газа относительно жидкости, то есть скорость жидкости на границе между газом и газом (при движении в противотоке).Но поскольку эта скорость на границе раздела обычно неизвестна, мы просто получаем скорость потока газа относительно стенки колонны. Другим способом получения данных о коэффициенте массопереноса в трубах является использование труб, отлитых из нескольких растворимых веществ, через которые проходит соответствующий растворитель. Или вы можете легко отлить трубу из легковоспламеняющегося материала и пропустить газ.
В обоих случаях, чтобы избежать значительного увеличения диаметра трубы во время эксперимента, необходимо использовать твердое вещество, растворение или сублимация которого очень slow. In в системах, где имеется поток жидкости, коэффициент молекулярной диффузии жидкости составляет всего 10 мин. 1, поэтому результаты обычно получаются с более высоким числом Шмидта (8c «a 1»), чем поток газа (8c «a 2000»). Ламинарный flow. It было отмечено, что массоперенос в ламинарном потоке в ваших 34 трубах можно рассчитать по данным, приведенным в п. 24 для того же потока теплопередачи.
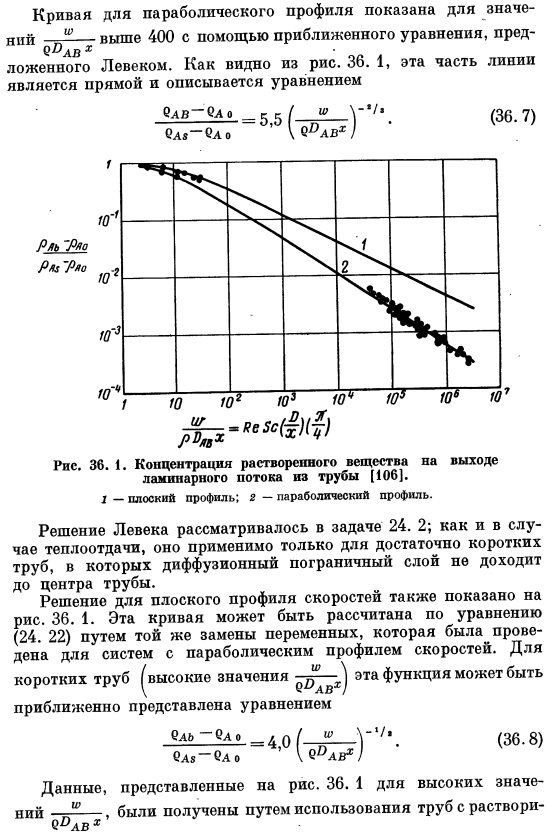
Теплопередающие решения даны для систем с плоскими параболическими профилями скоростей как для постоянной температуры стенки, так и для постоянного теплового потока. Здесь концентрация вблизи стенки считается постоянным раствором, как и раствор, когда температура стенки постоянна. Решение не принимается во внимание, когда поток материала от стенки постоянен. На рисунке показано полное решение Гретца относительно концентрации pAB, когда существует постоянная концентрация вблизи стенки и имеется параболический и планарный профиль скорости. 36.
Решение реализовано следующим образом: кривая, связанная с параболическим профилем скорости, была получена путем замены теплопередачи на массопереносное решение, аналогичное решению ГРЕТСА-уравнению (24. 19) уравнение к интегральному уравнению аналогичной концентрации(24. 18) относится к трубам поперечного сечения и интегрируется с ними. Аналогичное решение применительно к массопереносу — это просто уравнение (24.18), а не зависимая переменная*〜уравнение(24. 18) независимые переменные Это Берг. Отложенная стоимость Рисунок 36.1, отличающийся от этого- Он. Соответствует 8С.
Горизонтальная координата. Кривая профиля параболы имеет вид x-более 400, используя приближенную формулу, предложенную Levek. As вы можете видеть из рисунка 36. 1, эта часть линии является прямой линией, и Формула блв сл ₌ ₅₅ ЕА-0lo (36.7) (eOLv1) Левек решает вопросы 24. 2 был reviewed. It может применяться только для достаточно коротких труб, где диффузионный пограничный слой не достигает центра трубы, как в случае теплопередачи.
Решение плоского профиля скорости также показано на рисунке. 36. 1. Эта кривая рассчитывается по формуле (24. 22).Для коротких труб(высокие значения), эта функция может быть приблизительно представлена следующим уравнением: Данные приведены на рисунке. 36. если значение x велико, то 1 получается с помощью трубы с золем Стена наверху. Этот метод был применен с подсчетом Шмидта, близким к 3000.As как видите, полученные данные достаточно хорошо согласуются с теоретическими кривыми параболы profile. At более низкие значения, экспериментальные данные ближе к кривой, основанной на предположении плоского профиля скорости.
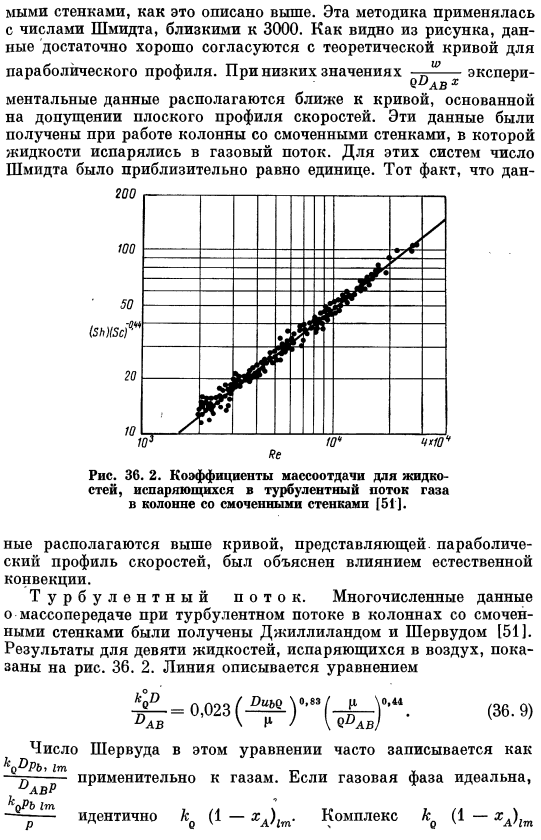
- Эти данные были получены при использовании колонны с влажными стенками, где жидкость испаряется в воздух. В этих системах счет Шмидта был почти равен 1. Дело в том, что Рисунок находится на кривой, которая представляет собой параболический профиль скорости и объясняется эффектами естественной конвекции. Турбулентность. Большое количество данных о массопереносе в турбулентных потоках во влажных колоннах было получено Джиллиландом и Шервудом [151].На рисунках показаны результаты 9 типов жидкостей, которые испаряются в воздух.
Прямая линия описывается следующим уравнением (36.9). Это номер Шервуда. 1 тонна — по отношению к ольвре . То же, что и 1. Уравнения часто описываются как газообразные. Если газовая фаза завершена,-chl )tt. комплексное число k (1-chl) ₁t Представляет собой коэффициент массы transfer. It не зависит от концентрации и сек. 33, таких как k₀. Кроме того, уравнение турбулентного массопереноса в трубе может быть получено из аналогии между массопереносом и импульсом, заданным в секундах. 35. Формула 35.
При конструировании систем охлаждения для транспортных ма-70 шин, в особенности для самолетов, приобретает особую важность решение проблемы максимального теплообмена при минимальном весе теплообменника. Людмила Фирмаль
Относится к коэффициенту трения следующим образом: Это уравнение основано на уравнении Колборна фактора/.Объединив эмпирическую формулу для коэффициента трения с формулой (35.28), получим уравнение, которое можно решить непосредственно относительно числа Шервуда. Уравнение (13. 72) имеет удобную форму для нанесения на гладкие трубы. / = Не 0.046″’». Когда эта формула объединяется с формулой (35.2), она выглядит следующим образом: 8б = 0.023, т. е. * «» 8В»».
Последняя формула дает результат, достаточно близкий к формуле предсказания (36.9), отличающийся только показателем степени числа Шмидта. Экспериментальные данные, приводящие к уравнению (36.9), получены в системе, где число Шмидта изменяется только от 0.6 до 2.5, поэтому показатель степени 0.44 равен suspicious. In при исследовании Линтопа и Шервуда, рассмотренных в разделе о ламинарном течении, было проведено несколько экспериментов в турбулентном режиме с числом Шмида 1000-2200.Эти результаты, наряду с данными Джиллиланда по мокрым стеновым столбам, показывают точное значение индекса числа Шмидта-0,33. Отсюда уравнение 36.
Потому что он может быть применен в более широком диапазоне, чем уравнение (36. 10) рекомендуем использовать. Уравнения Прандтля-Тейлора и кармана (13. 72) и в комбинации можно также получить уравнение для вычисления коэффициента массопереноса. Однако мы знаем, что уравнение Колборна дает в целом удовлетворительные результаты, и его преимуществом является простота. Коэффициент массопереноса уравнения (36.9) или (36.10) турбулентного течения может быть применен к определенным условиям развитой области течения или ко всей поверхности трубы, если длина превышает 50 диаметров. Коэффициент массопереноса на входе в трубу бесконечно велик, как и коэффициент теплопередачи.
Рыскание в области турбулентного движения В течение 10 лет коэффициент остается неизменным. Развитая подача обычно установлена под диаметром трубы, после чего Она постоянна по своей природе и равна той, которая вычисляется по уравнению. Если длина трубы превышает диаметр 50, то при большом значении коэффициента на входе процент суммарного массопереноса будет уменьшаться, а средний коэффициент всей трубы будет примерно равен локальному коэффициенту развитой области течения. Пример 36.2. Воздух проходит по трубам из нафталина диаметром 25,4 мм и длиной 1,83 м со скоростью 0,61 м / с и Б) 15,24 м / с. Температура воздуха составляет 10°С, среднее давление-1 Ат.
Учитывая, что перепад давления в трубе незначителен, а температура поверхности нафталиновой трубы равна С, необходимо найти в кг / ч степень насыщения воздуха нафталином и скорость сублимации нафталина в трубе. Характеристики воздуха при температуре 10°С и абсолютном давлении 1: Характеристики нафталина при 10°C: Коэффициент молекулярной диффузии в воздухе 1.86-10″ mHh; молекулярная масса 128.2. А) b = 0,61 м / с: 0,0254-0,61• 1.785 — » г» * = 1080 Ламинарный поток); 1.785-10 — » — 3600_₂₇₇. Согласно рисунку 36.1 о кривой профиля параболы Пр-0la потока.- Оло. = 0,42 Предполагается, что воздух, поступающий в трубу, не содержит нафталина, то есть pA₁= 0.
Концентрация нафталина Выходить. Воздух Скорость сублимации eA₁₁= 0.42•1.52•10- * = 0.64-10- * кг / м. NAFSA —. 0.0254 •0.61•0.64 −10-*-3600 = 7.12■10 «кг / ч. Четыре Степень насыщения выхлопа составляет 42%. b) b = 15,24 м / с; „0,0254-15.24 −1.249 Ева-1. 7Ya5. 1Р-8 В турбулентности для определения коэффициента 1 применяется уравнение (36.10). 8b = 0,023■(27,000) ⁰ •(2.7 7)*-3= 0.023•3500■1.40 = фр.
Поскольку молярная доля нафталина в воздухе очень мала(1-chl> 1t “ & * ■следовательно= k、 113-1. 86-10». * «- — — — — — — 0L254 — — — — — ⁸2 ′ ⁷ * / H ’ Для бесконечно малых сегментов труб описан баланс мохового шара материала. Из-за низкой скорости сублимации объемный поток можно считать независимым от расстояния от входа до трубы.
Смотрите также:
| Межфазная турбулентность | Коэффициент массоотдачи при движении двухфазного потока в слое насадки |
| Применение анализа размерностей к массопередаче | Массоотдача от шариков и цилиндров |

