Оглавление:



Коэффициент восстановления температуры в разреженном газовом потоке
- При больших потоках разреженного газа тепловой поток к стенке или от нее определяется по формуле (10.20) для плотной medium. To рассчитайте тепловой поток в этих условиях, коэффициент восстановления температуры g должен быть оценен. Эта величина зависит от степени разбавления газового потока. Исключив число М из формул (10.6) и (10.7), получим формулу для коэффициента восстановления температуры. Из отношений (11.19). Это легко найти по формуле(10.6 (11.32) (11.33) Если разделить выражение (11.32) на(11.33), то получится следующая формула: Коэффициент восстановления температуры Мистер стрим.
Тогда интегрирование дает: Для полностью стабилизированного потока в трубе следует применять среднюю скорость ит и объемную температуру 1В. Людмила Фирмаль
Свободная молекула Р (11.34)) Из этой формулы можно получить формулу, которая позволяет вычислить r 1 для объекта различной формы. Поэтому в случае пластины, которая находится под углом Р относительно свободного молекулярного потока、 x V l(25 * +1) 5-5Sh r. ep («- Yap R)+25 » a | p’R (₽/сотового-₽ — клетки-клетки-клетки-клетки-клетки-клетки-клетки)(«это не так. №₽)+ е -, н * (11.35 утра)) если p = 0, то эта форма ГееГ» — коэффициент восстановления в плотном ламинарном состоянии flow. It равно 0,94. г-коэффициент восстановления промежуточной области.
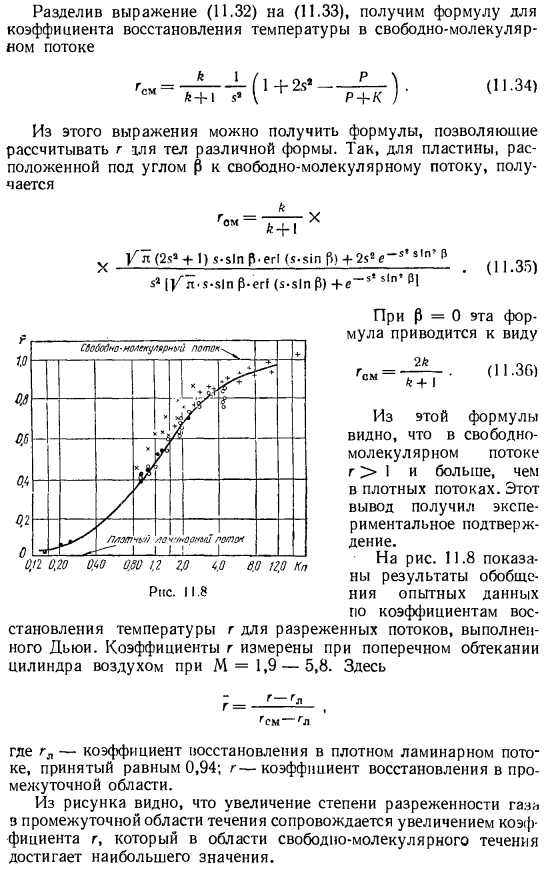
- Из рисунка видно, что увеличение степени разрежения газа из Средней области течения сопровождается увеличением коэффициента р, которое достигает наибольшего значения в области свободномолекулярного течения. Фазовый переход вещества(кипение, испарение, конденсация, сублимация) сопровождается значительным изменением условий теплообмена вблизи поверхности. Переход теплоносителя из одного агрегатного состояния в другое влияет на механизм и интенсивность теплопередачи. При подаче газа в пограничный слой через пористые стенки отсутствует фазовый переход хладагента, но механизм теплопередачи имеет много общего с теплопередачей при испарении.
В произвольной плоскости, параллельной поверхности стенки, а следовательно параллельной оси х, в пределах ламинарного подслоя существует напряжение сдвига Согласно уравнению (2-2) тепловой поток на единицу площади для плоскости определяется следующим образом: Теперь рассмотрим плоскость, параллельную стенке в турбулентном потоке. Людмила Фирмаль
Поэтому в данной главе также рассматривается теплообмен при введении вещества в пограничный слой. Процесс теплопередачи, когда изменяется состояние агрегата и в пограничный слой вводятся посторонние вещества, имеет большое значение в авиационной и ракетной технике.
Смотрите также:

