Оглавление:




Коэффициент теплоотдачи в химически равновесных реагирующих средах
- В локальном химическом равновесии система дифференциальных уравнений, описывающая процесс теплообмена между стенками и газами химической реакции, имеет тот же вид, что и в случае инертного теплоносителя. Как отмечалось выше, при локальном химическом равновесии дифференциальное уравнение массы массы не определяет изменение концентрации компонентов в потоке, поэтому его нельзя рассматривать. Уравнения непрерывности и движения имеют ту же форму, что и в случае инертного теплоносителя. Понятие эффективной теплоемкости позволяет придать инертному теплоносителю ту же форму, что и в дифференциальном уравнении (9.30 ₁ — ^- =C11U(X: ₁fyga.
Реактивное дифференциальное уравнение теплопередачи (9.33) может дать такой же вид инертности Где c ^₈ф-среднее значение изобарной эффективной теплоемкости смешанного газа в диапазоне температур от T до TSH. Поэтому теплообмен в реактивном газе и инертном потоке в локальном химическом равновесии описывается одним и тем же уравнением. Этот вывод позволяет использовать теоретические и экспериментально полученные формулы для исследования теплообмена в инертной среде потоков химических реакций, просто заменив X, cp, a на Hvf, S. И avf.
Во-вторых, расчетные и опытные данные трудно сравнивать потому, что часто при низких скоростях, характерных для ламинарного потока, вихревые токи свободной конвекции изменяют ламинарный характер движения: в результате получается сочетание свободной и вынужденной конвекции Л. Людмила Фирмаль
Таким образом, если для инертной среды получено уравнение подобия (9.46) Затем его можно использовать для оценки теплопередачи химически реагирующих газов.、 Куда? N4 ^ etPr? ф、 (9.47) RGVF По термам деление уравнения (9.47) на (9.46、 ^»(T1s? Где » — коэффициент теплопередачи инертной (реактивной) среды. Теплофизические свойства реакционной среды X ^ X и c1 ^ cn могут изменяться в широком диапазоне, а изменения температуры могут иметь немонотонный характер properties. So, в Формуле (9.48) логично использовать среднее интегральное значение этих характеристик.
Затем мы перепишем формулу (9.48) следующим образом: Где a * — a-D -, I X ^ f, X’, c)) и c ’ — средние интегральные значения параметров. Коэффициент a *также представляет собой коэффициент теплопередачи химической среды. Только при использовании уравнения для плотности теплового потока(9.18) следует записать в виде: 7 =(9.50) Для* 0 средняя интегральная характеристика реагирующей среды стремится к своему локальному значению-разности температур между средой и стенкой реактора. ДТ. In при этих условиях формула (9.49) сводится к следующему виду: В§ 5 этой главы было показано, что влияние химической реакции на коэффициент теплопередачи отражается числом B.
- Из уравнений (9.46) и(9.47) видно, что влияние Ke и Pr на коэффициент теплопередачи равновесной реакционной среды и нереакционной среды одинаково. Из этого можно сделать вывод, что «С ней» (9.52) Сюда! Выражение (9.52)справедливо для DT — > 0, так как _E-это локальное значение Lyops-счетчик Семенова. Коэффициент зависимости (9.52) может быть определен с помощью формул (9.41) и (9.51).1 Определите количество оценок A * / A и 2 Определите количество быть. Эта зависимость стала очевидной на основании расчетных оценок количества диссоциативных реакций X₉₁₁/ X и S, EPH / SR ОО 3 ^ — л 4 и а/ л л НYAЯ.
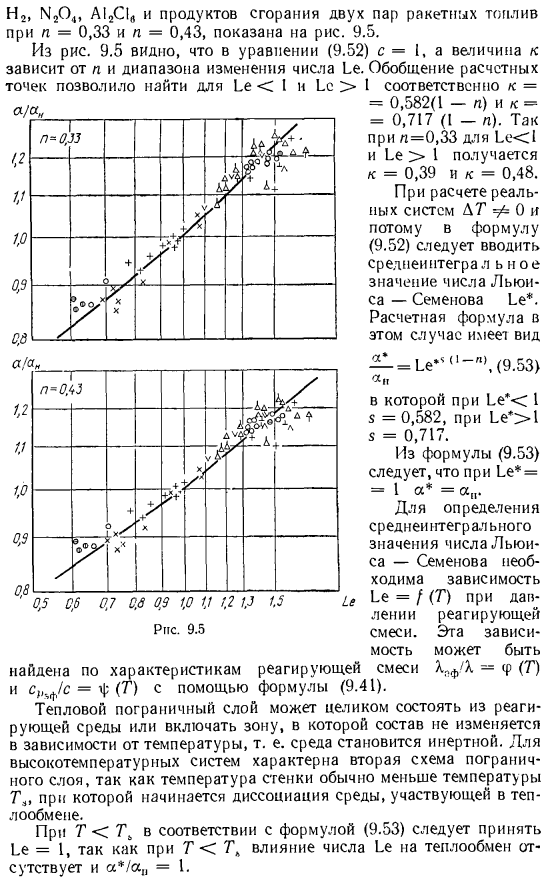
На рисунке показано 0,33 из 2 комплектов ракетного топлива при n = 0,43 и l = A1₂С1в и продукте сгорания. 9.5. Из рисунка видно, что в уравнении 9.5 (9.52) c = 1, но величина k зависит от диапазона переменных n и числа 1_e. обобщение вычислительных точек позволило найти k = 0.582(1-n) и k = 0.717 (I-n) соответственно для b и bc> I. So, для n = 0,33, для bf 1 и bf 1: При расчете реальной системы необходимо ввести среднее интегральное значение числа Льюиса-Семенова 1_e *в Формулу (9.52), так как DT = 0.Формула в этом случае имеет вид^ — = b * * 1〜 » ’(9.53), где b * * 1, x = 0,582, А b 1 5 = 0,717.
Если теплоотдача происходит от жидкости к стенке, слои у стенок трубы обладают большей вязкостью, чем в основном ядре потока, поэтому скоростное поле описывается кривой с. Людмила Фирмаль
Из Формулы (9.53), b * * * * = Для определения среднего интегрального значения числа Льюиса-Семенова необходимо иметь зависимость 1_ebe= /(Г) от давления реагирующей смеси. Это зависит Р-0,93 В г * икс » Ма я—— 1-1 я не уверен. — И 0.5 0.6 O. 7 0.8 0.9 1.0 1.1 1.21.3 1.5 Используя формулу (9.41), можно узнать возможности из свойств Xpf / X- (T) и Cpf / c =φ (T) реакционной смеси. Термический пограничный слой может полностью состоять из реакционной среды или содержать зоны, в которых состав не изменяется в зависимости от температуры, то есть среда становится инертной.
Для высокотемпературных систем характерна схема пограничного слоя 2-го типа, так как температура стенки обычно ниже температуры т, при которой начинается диссоциация среды, участвующей в теплопередаче. При T T, согласно формуле (9.53), необходимо принять L = 1.Потому что в TT нет влияния числа L e на теплопередачу и a * / a = 1. ТС Он не легко поврежден. Для Tm> T первый член в этом выражении должен быть равен нулю Необходимость изучения теплообмена на высоких скоростях Движение газа во многом определяется развитием авиации и ракетостроения technology.
Смотрите также:

