Задача №1.2.9. Клин массой 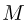с углом при вершине может двигаться поступательно по вертикальным направляющим (см. рисунок).

Задача №1.2.9.

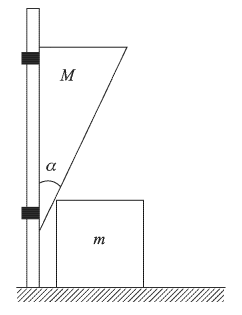
Клин массой с углом 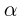при вершине может двигаться поступательно по вертикальным направляющим (см. рисунок). Боковой стороной он касается кубика массой 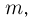лежащего на горизонтальной поверхности. Найти ускорение 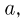с которым будет двигаться клин, если его отпустить. Трением между всеми поверхностями пренебречь. Ускорение свободного падения .

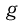Решение:

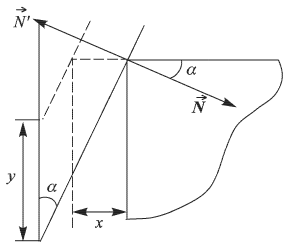
Силы, действующие на клин и кубик, изображены на рис. А, где приняты следующие обозначения: 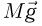и 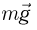— силы тяжест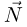и, и 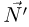— силы взаимодействия клина и кубика, 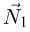— сила реакции стола, 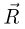— сила реакции вертикальных направляющих. Силы

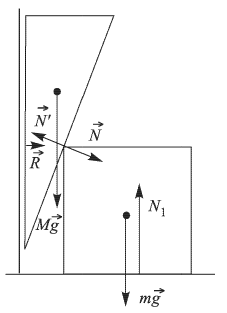
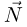и 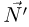направлены перпендикулярно поверхности клина, т.к. трение отсутствует. По третьему закону Ньютона 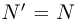. Обозначив через 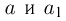ускорения клина и кубика, запишем уравнения движения этих тел:

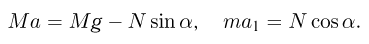
Из рис. Б видно, что перемещения кубика и клина за любой промежуток времени связаны соотношением 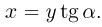Дважды дифференцируя это соотношение по времени, находим, что,

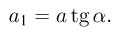
Исключая из уравнений движения 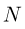и используя соотношение между величинами ускорений клина и кубика, получаем ответ:

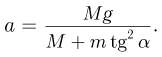
Эти задачи взяты со страницы решения задач по физической механике:

Решение задач по физической механике

Возможно эти задачи вам будут полезны:

Задача №1.2.7. Невесомая пружина скрепляет два груза с массами и Когда эта система подвешена за верхний груз, длина пружины равна Если систему поставить на подставку, длина пружины будет равна Определить длину ненапряженной пружины.

Задача №1.2.8. Наклонная плоскость, образующая с горизонтом угол , движется с ускорением а, направленным влево, как показано на рисунке. При каких значениях тело, находящееся на наклонной плоскости, будет скользить вверх вдоль нее? Коэффициент трения между телом и плоскостью.

Задача №1.2.10. К грузику массой прикреплена пружина, другой конец которой привязан к нити, перекинутой через блок. На втором конце нити подвешен грузик массой Когда блок заторможен, длина пружины Какую длину будет иметь пружина, если блок освободить? Считать, что колебания в системе не возникнут, т.е. грузики будут двигаться с постоянным ускорением. Длина недеформированной пружины Массой пружины, нити и блока, а также трением в блоке пренебречь.

Задача №1.2.11. На горизонтальном столе находится брусок массы , которому привязана нерастяжимая нить. Второй конец нити перекинут через блок и прикреплен к грузу массы . Коэффициент трения между бруском и столом . Пренебрегая массой блока, определить силу , с которой нить действует на блок.