Классификация особых точек. Связь между нулем и полюсом функции
Как уже знаем, особой точкой функции  называется точка, в которой функция не является аналитической.
называется точка, в которой функция не является аналитической.
Особая точка 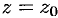 функции
функции  называемся изолированной, если в некоторой окрестности ее функция
называемся изолированной, если в некоторой окрестности ее функция  не имеет других особых точек.
не имеет других особых точек.
Если  — изолированная особая точка функции
— изолированная особая точка функции  , то существует такое число
, то существует такое число 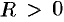 , что в кольце
, что в кольце 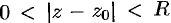 функция
функция  будет аналитической и, следовательно, разлагается в ряд Лорана (76.11):
будет аналитической и, следовательно, разлагается в ряд Лорана (76.11): 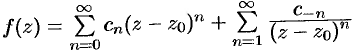 .
.
При этом возможны следующие случаи:
1) Ряд Лорана не содержит главной части, т. е. в ряде нет членов с отрицательными показателями. В этом случае точка  называется устранимой особой точкой функции
называется устранимой особой точкой функции  .
.
2) Разложение Лорана содержит в своей главной части конечное число членов, т. е. в ряде есть конечное число членов с отрицательными показателями. В этом случае точка  называется полюсом функции
называется полюсом функции  .
.
3) Разложение Лорана содержит в своей главной части бесконечное множество членов, т. е. в ряде есть бесконечно много членов с отрицательными показателями. В этом случае точка  называется существенно особой точкой функции
называется существенно особой точкой функции  .
.
Укажем особенности поведения аналитической функции  в окрестности особой точки каждого типа.
в окрестности особой точки каждого типа.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интеграл Коши. Интегральная формула Коши |
| Нули аналитической функции |
| Устранимые особые точки |
| Существенно особая точка |

