Оглавление:






Классификация связей. Число степеней свободы. Классификация сил
- Классификация отношений.Классификация числа степеней свободы сил Система материальных точек называется несвободной, и на их движение накладываются некоторые ограничения (ограничения) (координаты, скорость, ускорение). Все механизмы являются примерами собственных систем материальных точек.
Отношения называются объектами, которые накладывают ограничения на координаты, скорость и ускорение точек материальной системы.Коммуникация делится на двустороннюю и одностороннюю. Коммуникация называется двусторонней (hold), когда она препятствует движению важных точек в одном направлении и в другом направлении. Примером двухстороннего общения является идеальный (невесомый тип Zee) стержень, но на его концах есть 2 важных момента: игнорировать важный момент я не могу приблизиться друг к другу, держаться подальше друг от друга и друг от друга.Если какой-либо из материалов 、
Такое соединение получается при замене идеального ядра ОА на напиток в предыдущем примере. Людмила Фирмаль
Например, чтобы зафиксировать точку О (рис. 140), 2-я точка А может двигаться по кривой, которая находится на сфере с радиусом, равным длине идеального стержня.То есть координаты точки А связаны зависимостью: =0.Таким образом, геометрические связи с обеих сторон выражаются в следующих соотношениях: Фигура МО. Координаты точек материальной системы: Зл> …Джей футов…> УП> 2л) = °- Соединение препятствует движению материальных точек в определенном направлении, но если вы позволяете им двигаться в противоположном направлении, то это называется односторонним (и удерживающим).
Тогда точки O и двигаться Мы не можем делать это друг от друга.、 — С момента пожара Это позволит нити сморщиться (рис. 141). Форма уравнения а для однонаправленной связи имеет вид / [> is(4 / (равно Растянутое состояние нити.Таким образом, односторонняя связь выражается в виде неравенства: ДЖЕЙ СИ*! «YI» 2 … «Л’ Л> Г к• 2К> * * * > > хп> г ТВ ЗН)^ Отношения также делятся на неустойчивые (зависящие от времени) и устойчивые (зависящие от времени). Если выражение соединения содержит время явно, соединение называется нестационарным. (‘У, И J2,… Си> Ык, ж} …, хп УП, ЗН, я)= 0 (R неявно, координаты точек в движении системы, как правило, являются、
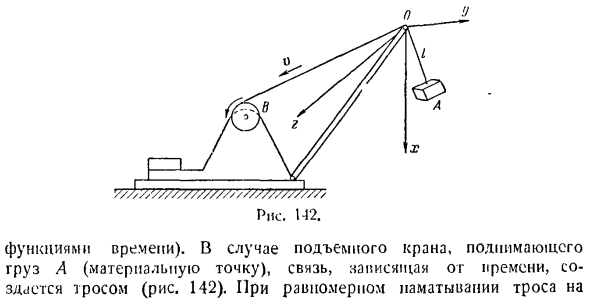
- Н Денпасар Да. Рисунок 1-12. В случае подъема краном груза а (важный момент) соединение производится кабелем или по времени (рис.142).С кабелем обернутым равномерно Скорость V барабана, длина подвесной части кабеля изменяется в соответствии с законом л = ЛК-ВТТ / 0-длина подвешенной части кабеля в первый момент.Поскольку нагрузка может колебаться, уравнение этой связи является pid x % — mV + z \ — (f0-vtf = 0, то есть оно явно включает время. Если выражение ссылки явно не содержит пробелов, то ссылка называется статической (во всех примерах, кроме приведенных выше, за исключением последнего, ссылка не зависит от времени).
Связь также делится на голономную и неголономную.Gadop(integrable) — это связь, которая накладывает ограничение на расположение точек материальной системы (конечно, после дифференцирования уравнений связи время может также приобретать связь между координатами точек системы и скоростью). Их соединение (называемое интегрируемым) называется соединением, которое накладывает ограничение на скорость движения точек системы. Oli представляет собой отношение между координатами и скоростью точек системы.
Поэтому твердое тело, вращающееся вокруг неподвижной оси, имеет 1 степень свободы. Людмила Фирмаль
Независимо от дифференциального уравнения движения системы, уравнения этих связей не могут быть интегрированы. Примером нехорологической системы является шар, который катится по шероховатой плоскости. Под совместными частотами системы материальных точек, подчиненных голономной связи, мы понимаем число независимых параметров, однозначно определяющих расположение точек в системе.Положение этого твердого тела, угол поворота<? вокруг оси нрашейя.
Есть 3 степени свободы для твердого тела, чтобы выполнить плоское движение. Потому что положение сечения, нарисованного параллельно неподвижной плоскости, определяется центроидом поперечного сечения xc и 2 координатами усов и угла. Система с 3 степенями свободы-это твердое тело, которое вращается вокруг неподвижной точки. Его положение определяется тремя углами Эйлера f и 0. Система из 6 степеней свободы является свободным твердым телом, так как ее расположение определяется 6 независимыми параметрами.3 барицентрические координаты xc, zc, 3 угла Эйлера<p,^, 0.
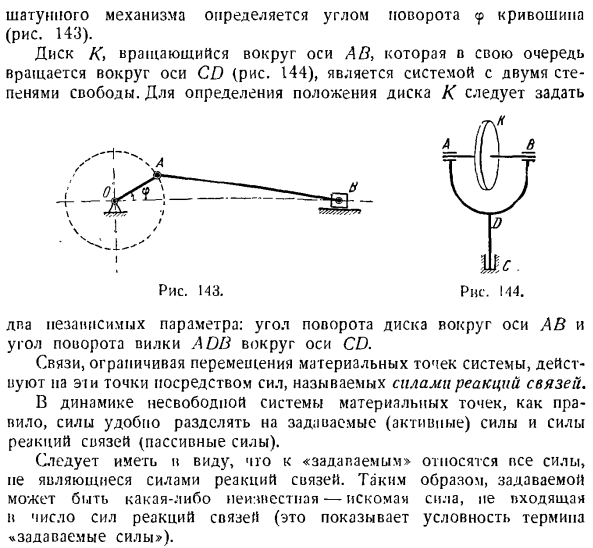
В упругом теле существует бесчисленное множество степеней свободы. Большинство механизмов представляют собой системы с 1 степенью freedom. So положение коленчатого вала Механизм шатуна определяется углом поворота кривошипа<p (рис. 143). Диск K}, который вращается вокруг оси AB, вращается вокруг оси CD (рис. 144) и представляет собой систему из 2 степеней свободы. Для определения положения диска необходимо задать значение K Все силы прилагаются способом, определяемым силой, которая не является условным термином
Из рисунка. 2 независимых параметра: угол поворота диска вокруг оси AB и угол поворота вилки ADB вокруг оси CD. Связи, ограничивающие движение материальных точек в системе, воздействуют на эти точки через силу, называемую связывающей реакцией force. In вообще, в динамике несвободной системы материальных точек удобно разделить силу на заданную (активную) силу и силу комбинированной реакции (пассивную). Следует иметь в виду, что»искомое» не является комбинированной реакцией force. It может быть неизвестно-найти количество сил реакции связывания (это указывает на указанную силу^»).
Принцип состоит в том, чтобы освободить спицы от Join. In в вопросе о динамике несвободной системы материальных точек мы используем принцип освобождения связи от связи. Это уже было применено к статическим проблемам. Система мысленно разрушает наложенную связь и включает противодействующую силу связи в указанное число forces. In в этом случае несвободной системой материальных точек считается свободная система, которая движется под действием заданной силы и силы связывающей реакции.
Когда система движется, сила реакции связи, в общем случае, переменна. Они зависят от расположения точек, их скорости, ускорения и времени. Это значительно усложняет решение приложенной силы, то есть обратной задачи, в которой движение точек системы определяется в зависимости от силы комбинированной реакции в системе. particular.
In для решения таких задач необходимо исключить объединенные силы реакции из системы дифференциальных уравнений движения. После нахождения движения точек системы, и, как следствие, скорости и ускорения, можно сигнализировать величину силы комбинированной реакции.
Смотрите также:
Предмет теоретическая механика
| Динамика плоского движения твердого тела | Метод кинетостатики |
| Теорема об изменении кинетической энергии системы материальных точек | Давление вращающегося твердого тела на ось вращения |

